本科生《统计计算》教材，采用R语言和Julia语言，包括误差

某些非随机的问题也可以通过概率模型引入随机变量， 化为求随机模型的未知参数的问题。 §3.1中用随机投点法估计\(\pi\)就是这样的一个例子。

随机模拟解决非随机问题的典型代表是计算定积分。 通过对随机模拟定积分的讨论， 可以展示随机模拟中大部分的问题和技巧。 随机模拟积分也称为蒙特卡洛(Monte Carlo)积分(简称MC积分)。 实际上，统计中最常见的计算问题就是积分和最优化问题。

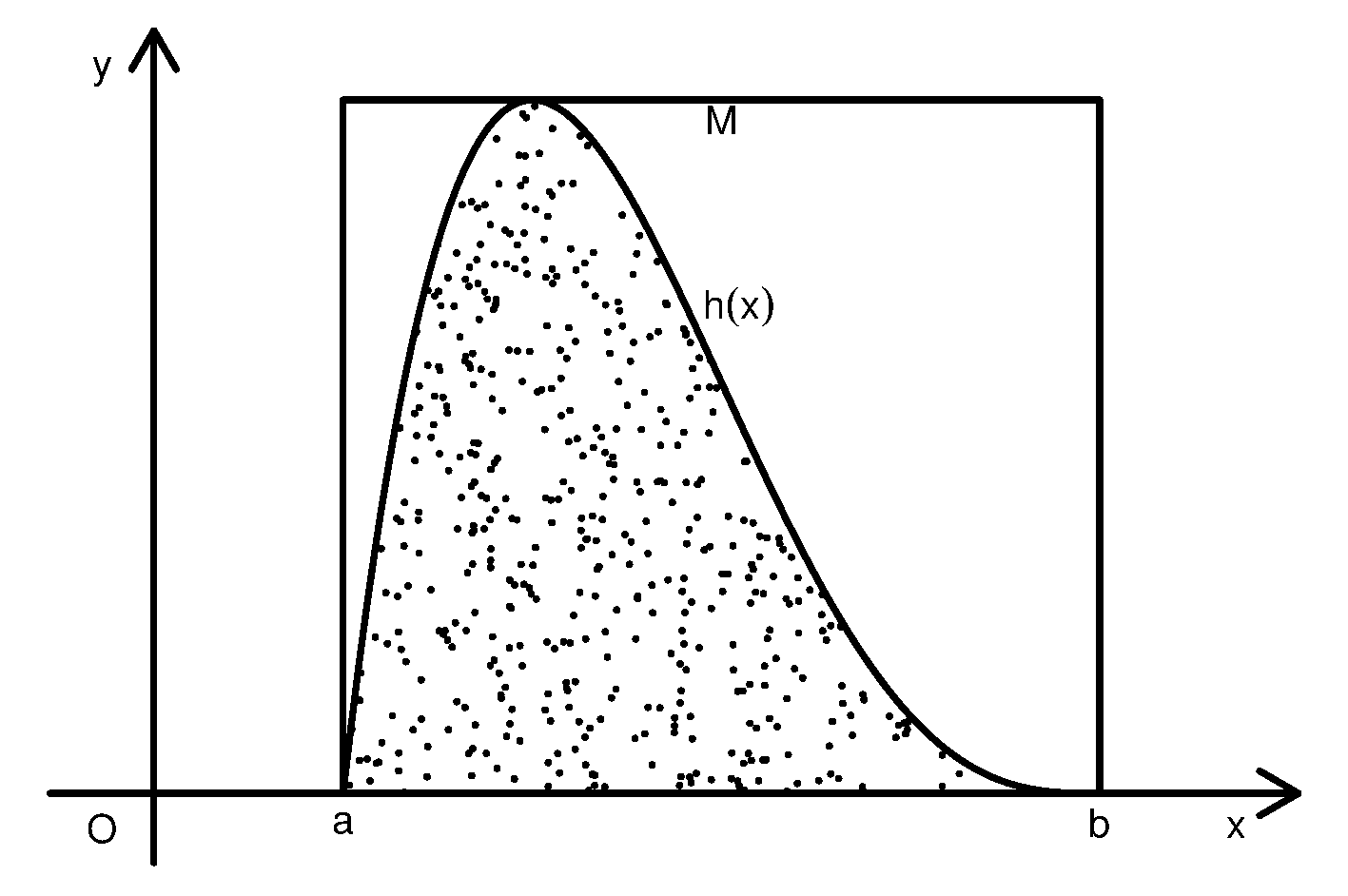
设函数\(h(x)\)在有限区间\([a,b]\)上定义且有界， 不妨设\(0 \leq h(x)\leq M\)。 要计算\(I=\int_a^b h(x) dx\)， 相当于计算曲线下的区域\(D=\{(x,y): 0 \leq y \leq h(x), x \in C = [a,b]\}\) 的面积。 为此在\(G = [a,b]\times(0,M)\)上均匀抽样\(N\)次， 得随机点\(Z_1, Z_2， \ldots, Z_N\)， \(Z_i = (X_i, Y_i), i=1,2,\dots,N\)。 令 \[\begin{aligned} \xi_i = \begin{cases}1, & Z_i \in D \\0, & \mbox{otherwise}\end{cases}, \quad i=1,\ldots,N\end{aligned}\] 则\(\{ \xi_i \}\) 是独立重复试验结果, \(\{ \xi_i \}\) 独立同 b(1,\(p\))分布，\[\begin{align} p = P(Z_i \in D) = V(D)/V(G) = I / [M(b-a)]\tag{11.1}\end{align}\]

其中\(V(\cdot)\)表示区域面积。

从模拟产生的随机样本\(Z_1, Z_2， \ldots, Z_N\)， 可以用这\(N\)个点中落入曲线下方区域\(D\)的百分比\(\hat p\)来估计 中的概率\(p\)， 然后由\(I = p M (b-a)\)得到定积分\(I\)的近似值\[\begin{align} \hat I = \hat p M (b-a)\tag{11.2}\end{align}\]

这种方法叫做随机投点法。 这样计算的定积分有随机性， 误差中包含了随机模拟误差。

由强大数律可知 \[\begin{aligned} \hat p =& \frac{\sum \xi_i}{N} \to p, \ \text{a.s.}\ (N \to \infty) \\ \hat I =& \hat p M (b-a) \to p M (b-a) = I, \ \text{a.s.}\ (N \to \infty)\end{aligned}\] 即\(N\to\infty\)时精度可以无限地提高（当然， 在计算机中要受到数值精度的限制）。

那么，提高精度需要多大的代价呢？ 由中心极限定理可知 \[\begin{aligned} \sqrt{N}(\hat p - p)/\sqrt{p(1-p)} \stackrel{\mbox{d}}{\longrightarrow} \text{N}(0,1), \ (N\to\infty), \end{aligned}\] 从而\[\begin{align} \sqrt{N}(\hat I - I) = M(b-a) (\hat p - p) \stackrel{\mbox{d}}{\longrightarrow}\text{N} \big(0, [M(b-a)]^2 p(1-p) \big)\tag{11.3}\end{align}\]