一个二次函数它的对称轴 初三数学试卷及答案 2015年九年级数学上期末试卷（附答案）(3)

2014-2015学年辽宁省鞍山市九年级（上）期末数学试卷参考答案与试题解析一、选择题（共8小题，每小题3分，满分24分）1．关于x的一元二次方程x2－3x+m=0有两个不相等的实数根，则实数m的取值范围为（）A．????B．????C．????D．??

考点：二次函数的三种形式．??分析：利用配方法整理即可得解．解答：解：y=2x2－8x－1，=2（x2－4x+4）－8－1，=2（x－2）2－9，即y=2（x－2）2－9．故选C．点评：本题考查了二次函数的三种形式，熟练掌握配方法的操作是解题的关键．5．如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，联结BC，若∠A=36°，则∠C等于（）??A．36°B．54°C．60°D．27°

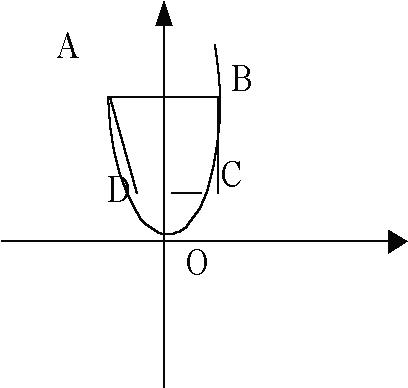
考点：直线与圆的位置关系．??分析：因为要使圆与斜边只有一个公共点，所以该圆和斜边相切或和斜边相交，但只有一个交点在斜边上．若d＜r，则直线与圆相交；若d=r，则直线于圆相切；若d＞r，则直线与圆相离．解答：解：根据勾股定理求得直角三角形的斜边是=13．当圆和斜边相切时，则半径即是斜边上的高，等于；当圆和斜边相交，且只有一个交点在斜边上时，可以让圆的半径大于短直角边而小于长直角边，则5＜r≤12．故半径r的取值范围是r=或5＜r≤12．故答案为：r=或5＜r≤12．点评：考查了直线与圆的位置关系，此题注意考虑两种情况，只需保证圆和斜边只有一个公共点即可．16．如图，点A，B的坐标分别为（1，4）和（4，4），抛物线y=a（x－m）2+n的顶点在线段AB上运动，与x轴交于C、D两点（C在D的左侧），点C的横坐标最小值为－3，则点D的横坐标最大值为8．??

考点：根的判别式．??专题：判别式法．分析：先根据判别式的意义得到△=（－3）2－4m＞0，然后解不等式即可．解答：解：根据题意得△=（－3）2－4m＞0，解得m＜．故选：B．点评：本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2－4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．2．某药品经过两次降价，每瓶零售价由100元降为81元．已知两次降价的百分率都为x，那么x满足的方程是（）A．100（1+x）2=81B．100（1－x）2=81C．100（1－x%）2=81D．100x2=81

考点：平行四边形的性质；相似三角形的判定与性质．??分析：利用平行四边形的性质得出AD‖BC，AD=BC，进而得出△DEF∽△DCF，再利用相似三角形的判定与性质得出答案．解答：解：∵四边形ABCD是平行四边形，∴AD‖BC，AD=BC，∴△DEF∽△DCF，∴=，∵点E是边AD的中点，∴DE=AE=BC，∴==．故答案为：1：2．点评：此题主要考查了平行四边形的性质以及相似三角形的判定与性质，得出△DEF∽△DCF是解题关键．14．如图，在矩形AOBC中，点A的坐标是（－2，1），点C的纵坐标是4，则B点的坐标为（，3）．??

??福建省漳州市龙海2017届九年级上期末数学试卷含答案解析17-08-02(试卷)

考点：二次函数综合题；解一元二次方程-直接开平方法；二次函数的性质；待定系数法求二次函数解析式．??专题：计算题；压轴题．分析：当C点横坐标最小时，抛物线顶点必为A（1，4），根据此时抛物线的对称轴，可判断出CD间的距离；当D点横坐标最大时，抛物线顶点为B（4，4），再根据此时抛物线的对称轴及CD的长，可判断出D点横坐标最大值．解答：解：当点C横坐标为－3时，抛物线顶点为A（1，4），对称轴为x=1，此时D点横坐标为5，则CD=8；当抛物线顶点为B（4，4）时，抛物线对称轴为x=4，且CD=8，故C（0，0），D（8，0）；由于此时D点横坐标最大，故点D的横坐标最大值为8；故答案为：8．点评：本题主要考查了二次函数的性质，用待定系数法求二次函数的解析式，用直接开平方法解一元二次方程等知识点，理解题意并根据已知求二次函数的解析式是解此题的关键，此题是一个比较典型的题目．三、解答题（共2小题，满分16分）17．解方程：x2－5x－6=0．