初中数学如何快速解决好等腰三角形问题，做到孰能生巧？

初中数学如何快速解决好等腰三角形问题，做到孰能生巧？

在初中数学中，我们在解决各种几何考题时，往往需要添加辅助线，集中转换分散的条件，寻找隐藏的条件，简化复杂的问题。

等腰三角形是初中数学的一个重点。等腰三角形相关的试题种类很多，题型也很多。

如何快速解决等腰三角形问题并做到完美？今天总结了以下四种常见的等腰三角形题相关的辅助线加法，一共5道到例题，有详细的解释。

方法一：三行合一。

三线合一是等腰三角形中最重要的性质定理之一。所谓三线是在等腰三角形中，顶角的角平分线，底的中线，底的高线。必须三行合一。

例1是最基本的三合一题型，D是BC的中点，然后连接AD，通过三合一的性质等腰三角形知识点及典型习题教案模板3，得到AD⊥BC。

第二种方法是做平行线法。这一般是一条腰的平行线，两个角相等，这样三角形就全等了。

在示例 2 中，这道题是非常常见的考试经典题型。在第一个子问题中，三角形全等，得到PD=QD。

第二个子题，经过点P做PF∥AC，因为△PBF是等腰三角形，PE⊥BF，三线合起来得到BE=EF。因为三角形是全等的，所以我们得到 FD=CD。因此得到ED=BC的一半，即固定值。

方法三：截长补空法，或截长取空法。

简单来说就是在某条线段上截取一条线段，等于已知线段。或者等腰三角形知识点及典型习题教案模板3，将一条线段扩展为等于已知线段。这种解题方法比较常用，请仔细研究，多探索，多练习。

示例 3 是扩展一条线段，使其等于已知线段，这是一种经典的考试题型。

例4，这是一个经典的试题类型，在某条线段上截取一条线段，等于已知线段，通过等值变换得出结论。

方法四：双半法，双中线法。

例5，分析说B点是BF||AC，最终结果是线段相等。

其实解决这个问题还有更好的办法，就是中心线相乘的方法。学生应在课后认真学习。

首先，让我知道如何添加辅助线。因为CE是△ABC的中心线，所以双倍长度中心线CE。将 CE 扩展到 F，使 EF=CE，连接 BF。当中心线加倍时，三角形必须全等，最后，△DBC≌△FBC，所以DC=CF，所以CD=2CE。

这是系列第2篇：引理部分可能有些地方有点劝退

前言：

其实我之前做过很多网红问题，而且都是在各大QQ群里流传，很奇怪的问题，现在突然想自己整理一下解决办法，当然我的解决办法比较笨，如果你有更好的办法，欢迎私信或评论区交流！

这是该系列的第二部分。也许这个问题严格来说算不上网红问题，但我还是很喜欢的。导数，就这么写吧！

下面是正文。

话题

X、Y、Z分别为线段AB、BC、CA上的点，满足：2YZ=BC，2ZX=CA，2XY=AB。证明：X、Y、Z 是三角形 ABC 边上的中点。

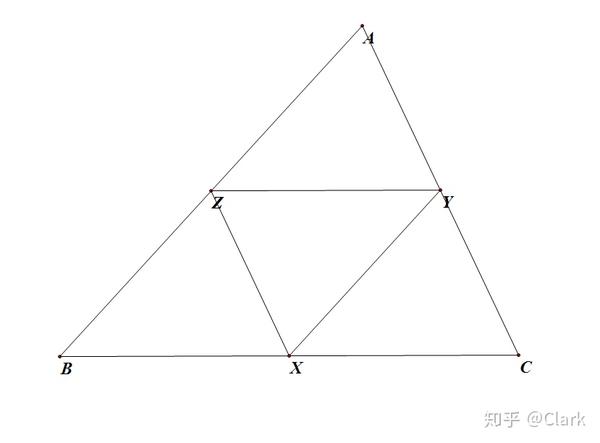
引理：

引理部分可能有些地方有点说服力，希望大家耐心观看！

1. 极惯性矩不等式：

设 P 是 △ABC 平面上的一个点，那么对于任意实数 \lambda、\mu、\nu，我们有：

(\lambda+\mu+\nu)(\lambda \cdot PA^2+\mu \cdot PB^2+\nu \cdot PC ^2)

\geq \mu \nu \cdot a^2 +\lambda \nu \cdot b^2+\lambda \mu \cdot c^2

其中等号为真当且仅当： \lambda \cdot \overline{PA} +\mu \cdot \overline{PB}+\nu \cdot \overline{PC}=0。

证明：

0 \leq \左| \lambda \cdot \overline{PA} +\mu \cdot \overline{PB}+\nu \cdot \overline{PC} \right|^2

=\sum{\lambda ^2 \cdot PA^2}+2\sum{\mu \nu \cdot \overline{PB} \cdot\overline{PC}}

\ =\sum{\lambda ^2 \cdot PA^2}+\sum{\mu \nu \cdot (PB^2 +PC^2-BC^2)}

\ =\sum{\lambda} \cdot \sum{\lambda \cdot PA^2}-\sum{\mu \nu \cdot a^2}

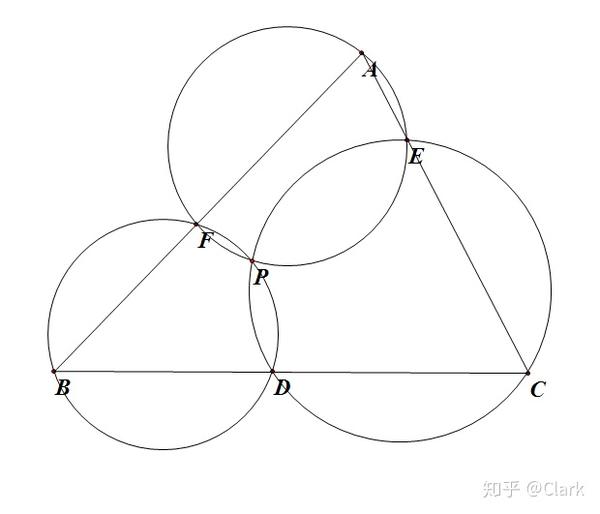
2. 三角形中的米克点：

若△ABC为三角形，三点D、E、F分别在边BC、CA、AB上，

则△AFE、△BDF、△CED的外接圆相交于点P。

3. 如果 O 是 \Delta ABC 的外心，则：

\sin 2A \cdot \overline{OA}+\sin 2B \cdot \overline{OB}+\sin 2C \cdot \overline{OC}=0

4.在\Delta ABC中，有：

\sin 2A+\sin 2B+\sin 2C=4\sin A \sin B \sin C

\tan A+\tan B+\tan C=\tan A \tan B \tan C

回答：

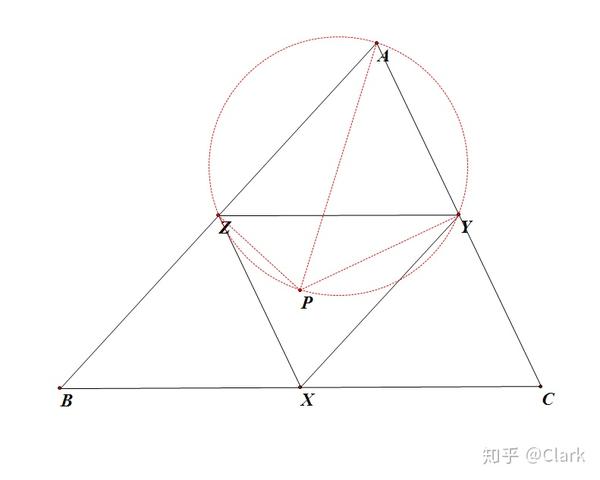
根据引理 2，我们不妨设 \Delta AYZ 、 \Delta BZX 、 \Delta CXY 外接圆相交于点 P

令 R 为 \Delta ABC 的外接圆的半径等腰三角形知识点及典型习题教案模板3，注意 A、Z、P、Y 是共圆的，

我们可以知道：PA的直径\leq\Delta AYZ=\frac{2YZ}{2\sin A}=\frac{a}{2\sin A}=R。

按照同样的方法，我们也可以知道：PB \leq R等腰三角形知识点及典型习题教案模板3，PC \leq R。

对于引理 1 中的不等式，我们取：

λ =\sin 2A，\mu=\sin 2B，\nu =\sin 2C

得到：

(\sin 2A+\sin 2B+\sin 2C)\次

(\sin 2A \cdot PA^2 +\sin 2B \cdot PB^2 +\sin 2C \cdot PC^2 )

\geq \sin 2B \ \sin 2C \cdot a^2+\sin 2C \ \sin 2A \cdot b^2 +\sin 2A \ \sin 2B \cdot c^2

让我们简化不等式的左右两边：

RHS=\prod \sin 2A \cdot \sum{\frac{a^2}{\sin 2A}}

=2R^2 \cdot \prod \sin 2A \cdot \sum{ \tan A }

=2R^2 \cdot \prod \sin 2A \cdot \prod{ \tan A }

=16R^2 \cdot (\prod{\sin A})^2

LHS=4\prod{\sin A} \cdot \sum{\sin 2A \cdot PA^2}

\leq 4R^2 \cdot \prod{\sin A} \cdot \sum{\sin 2A }

\ \ \ \ \ \ \ \ \ =16R^2 \cdot (\prod{\sin A})^2

然后： 16R^2 \cdot (\prod{\sin A})^2 \geq LHS

\geq RHS=16R^2 \cdot (\prod{\sin A})^2

因此，上述不等式的不等号都变成了等号。现在让我们关注平等条件：

1.\sin 2A \cdot \overline{PA}+\sin 2B \cdot \overline{PB}+\sin 2C \cdot \overline{PC}=0

2. PA=PB=PC=R

对于第一个条件，从引理 3 我们知道这表明 P 是 \Delta ABC 的外心

对于第二个条件，我们知道这意味着：PA 是 \Delta AYZ 的外接圆的直径

所以\angle AYP=\angle AZP=\frac{\pi}{2}，即PY\\bot\AC，PZ\\bot\AB，

又因为 P 是 \Delta ABC 的外中心，Y 和 Z 分别是 AC 和 AB 边的中点。同理，X也是BC边上的中点，证明！

晋升：

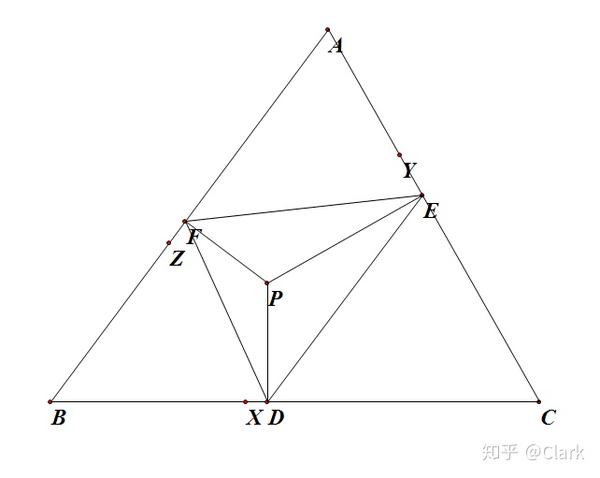
从上面的证明方法，我们可以做一个类比。对于米克点垂直于边上各点连线的边，且两点之间的距离为固定值，则三角形是唯一的。缩写如下：

P 是某一点，从 P 到 \Delta ABC 的三个边，我们可以得到 D、E、F。

如果 X 在 BC 上，Y 在 CA 上，Z 在 AB 上，这样：

XY=DE，YZ=EF，ZX=FD，

证明：\Delta XYZ 与 \Delta DEF 一致

写在最后：

还是祝各位即将高考的学姐学姐高考顺利！