初中几何:平面几何题目一般有这几种模型,模型/截长补短
初中几何:平面几何题目一般有这几种模型,模型/截长补短
几何是初中数学的难点。很多学生在课堂上虽然能听懂老师的讲解,但做不了几何题。其实最大的原因就是没有几何思维,知识薄弱。
老师将从以下三个方面教你如何在初中学习几何:
平面几何题一般有这几种模型,全等模型三竖直、三角形模型/全等模型半角模型/中点模型/手拉手模型/奔驰模型/相辅相成。在这里,老师整理了相关模型的知识点和例题,下次做的时候可以对应,做起来就得心应手了!
码字不易,如果你觉得不错,可以连续支持三遍!!
三个全等模型:垂直模型和三角形模型
三个垂直,三个等距模型
定义:由同一直线上的三个等角顶点组成的图形。这个角度可以是直角、锐角或钝角。一般以等腰三角形或等边三角形为背景。这个模型贯穿了初中的几何,也是三年级教“相似三角形”时很重要的一个知识点
方法细化
1 如果题中有一条直线和三个(直角)等角,可以直接证明边和角的转换可以通过相似或全等来实现;
2 如果标题中没有给出一条线和三个(直角)等角,可以根据需要构造
基本型号:(1)一排三竖排
【基本图形】
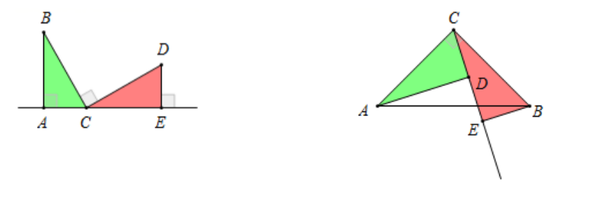
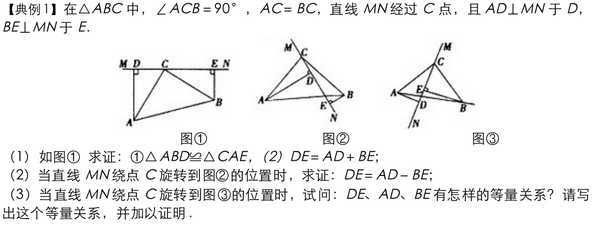
全等模型的半角模型
定义:半角等腰三角形知识点及典型习题教案模板3,顾名思义,就是一个大角夹着一个只有它一半大小的角,如下图所示。
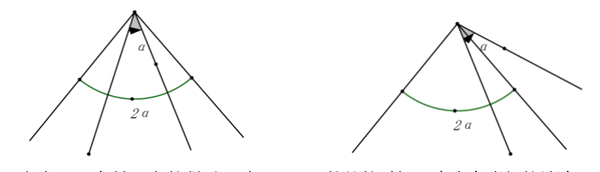
这种类型的主题有自己的固定方法。当a取不同的值时,会有相似的结论。
夹半角的常见分类:
(1) 90度夹45度
(2) 120度夹60度
(3) 2α夹α
题型:90度和45度
【例1】 如图,正方形ABCD中,E在BC上,F在CD上,∠EAF=45°,证明: (1) BE+DF=EF
(2) ∠AEB=∠AEF
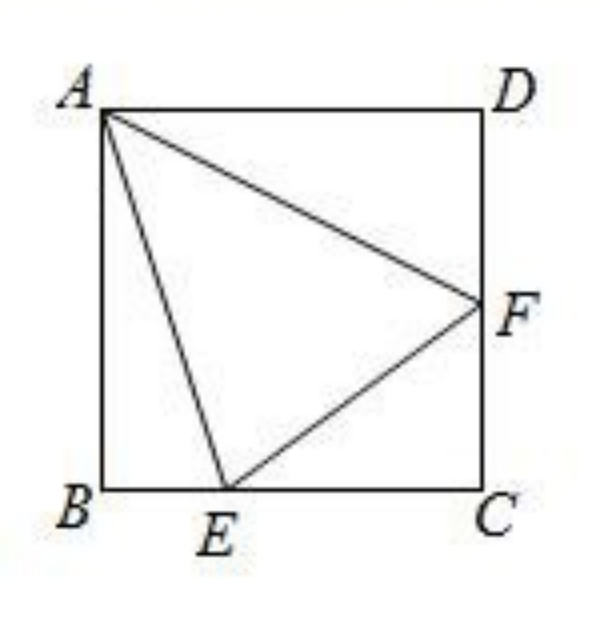
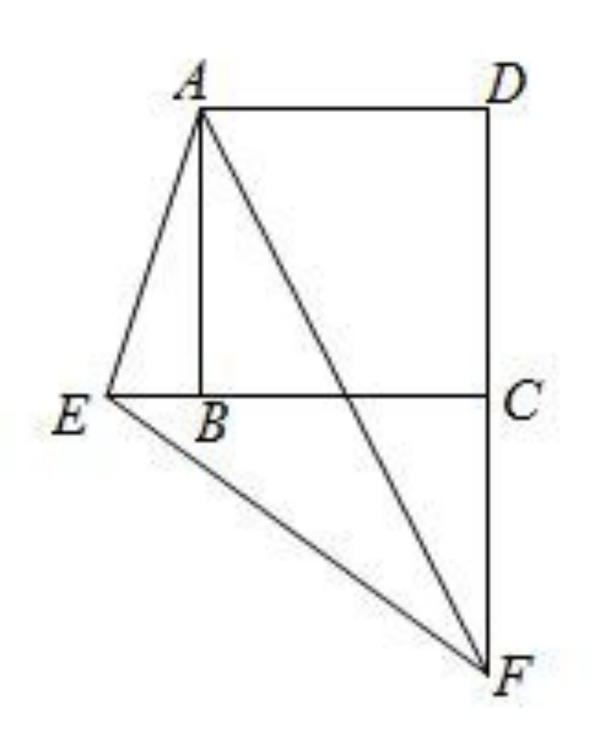
(2)在例1的条件下,如果E在CB延长线上,F在DC延长线上,其他条件不变,证明:
(1) DF-BE=EF
(2) ∠AEB+∠AEF=180°
中点模型
模型1.构造一个全等三角形,中线为双倍长度或中线状(与中点相关的线段)
如图①所示,AD为△ABC的中线。将 AD 扩展到 E 点,使 DE=AD。容易证明:△ADC≌EDB(SAS)。
如图②所示,D为BC的中点。将 FD 扩展到 E 点使得 DE=FD。容易证明:△FDB≌△EDC(SAS)。
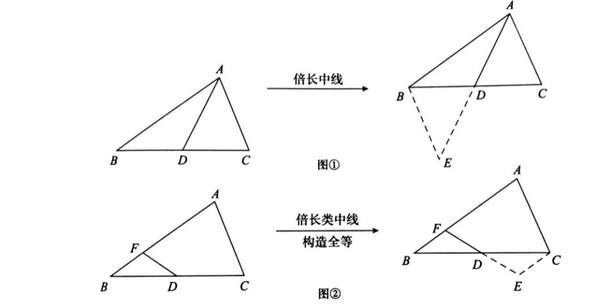
模型分析:
遇到中线或中点时,可以尝试用双长中线或双长中线构造全等三角形,以便在已知条件下转移线段。
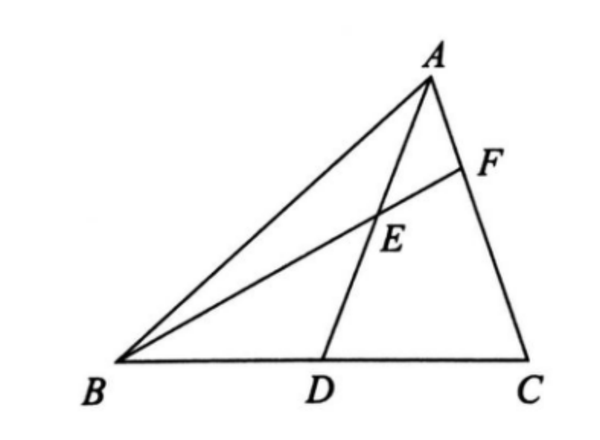
例1、如图所示,已知△ABC中,AD为BC边的中线,E为AD上的一点,连接BE并将AC延伸至F点,AF=EF。证明:AC=BE。
模型2.已知等腰三角形底边的中点,可以考虑用“三线合一”与顶点连接
模型分析:
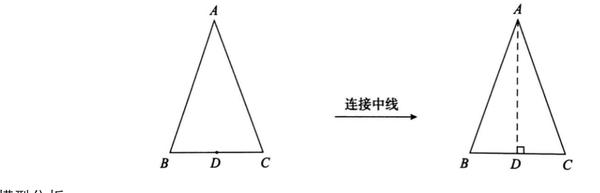
当等腰三角形有底的中点时,常将其作为底的中线,利用等腰三角形的“三线合一”性质,角相等或边相等。为解决问题创造更多的条件,当你看到一个等腰三角形时,你应该想到“边相等,角度相等,三线统一”。
例如,如图所示,在△ABC中,AB=AC=5,BC=6,M为BC的中点,MN⊥AC在N点,求MN的长度。
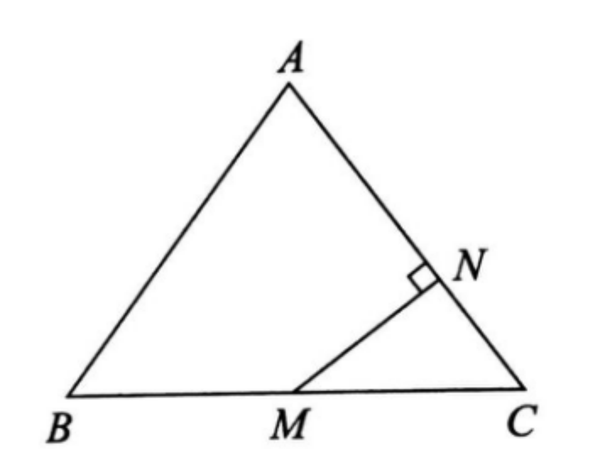
模型3.知道三角形一侧的中点,可以考虑中线定理

模型分析:
在一个三角形中,如果有一个中点,就可以构造出三角形的中线,可以利用三角形中线的性质定理:DE∥BC,DE=1/2BC来解题。中线定理既有线段之间的位置关系,也有数量关系。该模型可以解决线段之间的等角、对半、相等和平行的问题。
例子。在四边形ABCD中,AB=CD,E和F分别是BC和AD的中点,连接EF并延伸,分别与BA和CD的延长线相交于点M和N。证明:∠BME=∠CNE。
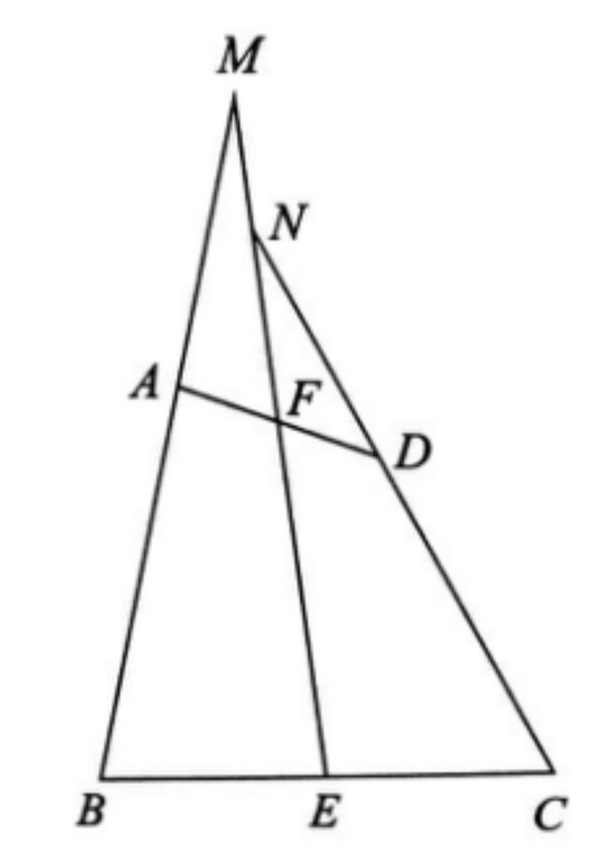
模型4. 知道直角三角形的斜边中点,可以考虑构造斜边中线

模型分析:
在直角三角形中,当遇到斜边的中点时,往往会画出斜边上的中线。直角三角形斜边上的中线等于斜边的一半,即CD=1/2AB,证明线段之间的数量关系。,可以得到两个等腰三角形:△ACD和△BCD,这个模型常与中线定理结合。
例如,如图所示,在△ABC中,BE和CF分别是AC和AB的高度,D是BC的中点,DM⊥EF在M点。证明:FM=EM。
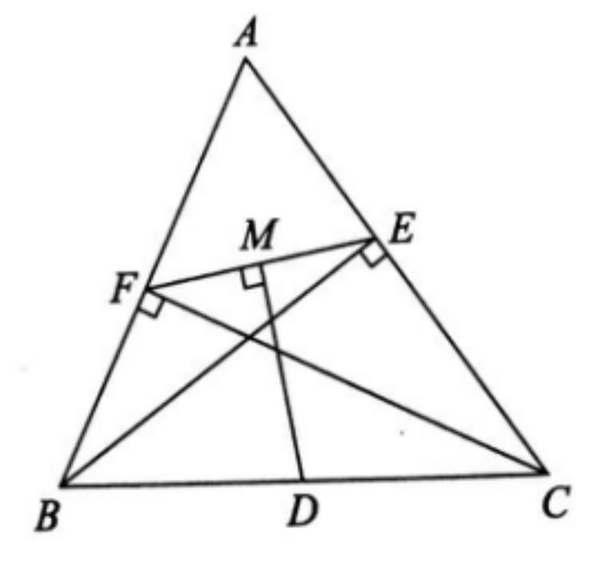
手拉手模型
例 1、在直线 ABC 的同侧作两个等边三角形△ABD 和△BCE,连接 AE 和 CD。证明:
(1) △ABE≌△DBC
(2) AE=DC
(3) AE与DC的夹角为60°。
(4) △AGB≌△DFB
(5) △EGB≌△CFB
(6) BH平分∠AHC
(7) GF∥AC
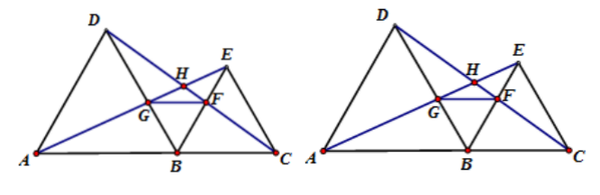
变式练习 1. 如果两个等边三角形 △ABD 和 △BCE 连接到 AE 和 CD,证明:
(1) △ABE≌△DBC
(2) AE=DC
(3) AE与DC的夹角为60°。
(4) AE与DC的交集为H, BH bisect ∠AHC
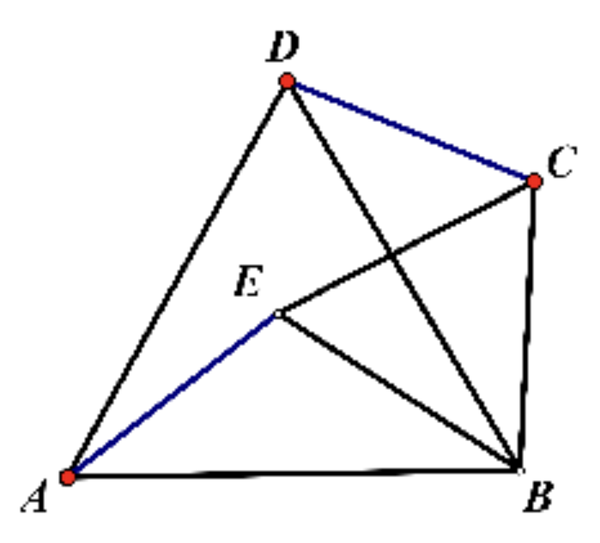
奔驰车型
截断长短
通过截断多头和补充空头来构造全等三角形
截长补短的方法是初中数学几何题中添加辅助线的方法,也是一种让几何题难易的思路。所谓“截断”,就是将三段中最长的线段一分为二,使其中一条线段与已知较短的两条线段之一相等,然后证明另一段与已知的。另一条线段相等;所谓“缩短”,就是将一条已知较短的线段延长到与另一条已知较短的线段相同的长度等腰三角形知识点及典型习题教案模板3,然后求延长线段与已知最长线段的差。关系。有的被拿来组成某个三角形来解决。
采用截长补短法作为辅助线,适用于证明线段的和、差、倍、分类。

老师每天都会分享优质的学习资料和学习方法。如果觉得有用,别忘了连续三天支持哦~~
电子版获取方式↓↓↓
zhuanlan.zhihu.com/p/124820262
易学熊数据库:涵盖初中全科学习资料-初中复习资料-中考综合复习等电子版学习资料
初中数学几何典型例题解决几何最值问题的通常思路(组图)

初中数学几何典型例子
求解几何极大值问题的总体思路
两点之间的最短线段;
在连接线外一点和线上所有点的线段中,垂直线段最短;
三角形两条边之和大于第三条边或三角形两条边之差小于第三条边(重叠时取最大值)
它是求解几何极大值问题的理论基础,根据不同特征进行变换是解决极大值问题的关键。通过变换和减少变量,更接近三个定理来解决问题;直接调用基本模型也是解决几何最大值问题的有效手段。
几何极大问题中的基本模型示例
轴对称最大值
图形
原则
两点之间的最短线段
两点之间的最短线段
三角关系
特征
A、B为不动点,l为固定直线等腰三角形知识点及典型习题教案模板3,P为直线l上的移动点,求AP+BP的最小值
A、B为不动点,l为定线,MN为直线l上的移动线段,求AM+BN的最小值
A、B为不动点,l为固定直线,P为直线l上的移动点,求|AP-BP|的最大值
兑换
是关于固定线 l 的固定点之一的对称点
先平移 AM 或 BN 使 M 和 N 重合,然后做一个不动点关于固定线 l 的对称点
是关于固定线 l 的固定点之一的对称点
折叠最有价值
图形
原则
两点之间的最短线段
特征
在△ABC中,M、N两点分别是AB、BC边上的动点。沿MN对折△BMN,B点对应点为B',连接AB',求AB'的最小值。
兑换
转换后求 AB'+B'N+NC 的最小值
2. 典型话题
1、如图:P点是∠AOB中的某一点,M点和N点分别在OA和OB边上移动。若∠AOB=45°,OP=

,则 △PMN 的周长最小值为 。
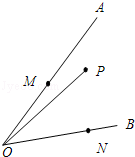
[解析] 取P 为OA 和OB 的对称点C 和D。连接 OC、OD。那么当M、N为CD与OA、OB的交点时,△PMN的周长最短,最短的值为CD的长度。根据对称性,可以证明△COD是一个等腰直角三角形,可以据此求解。
【答案】解:取P 关于OA 和OB 的对称点C 和D。连接 OC、OD。那么当M、N为CD与OA、OB的交点时,△PMN的周长最短,最短的值为CD的长度。
∵PC关于OA对称,
∴∠COP=2∠AOP, OC=OP
同理,∠DOP=2∠BOP,OP=OD
∴∠COD=∠COP+∠DOP=2(∠AOP+∠BOP)=2∠AOB=90°,OC=OD。
∴△COD是等腰直角三角形。
那么CD=

超频=

×3

=6。
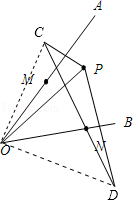
【题后思考】这道题考察了对称性的本质,把图形做对了,理解△PMN的最小周长条件是解题的关键。
2. 如图所示,当四边形 PABN 的周长最小时,a = .

【解析】因为AB和PN的长度是固定的,只要找到PA+NB的长度就够了。问题是何时 PA+NB 最短。
将 B 点向左移动 2 个单位到 B' 点;做一个B'关于x轴的对称点B",连接AB",在P处与x轴相交,确定N点的位置。此时PA+NB最短。
设直线AB"的解析式为y=kx+b,通过待定系数法可以得到直线的解析式。可以得到a的值。
[答案] 解法:将点N向左移动2个单位与P重合,将B点向左移动2个单位到B'(2,-1),
做B'关于x轴的对称点B",根据实践知道点B" (2, 1),
设直线AB″的解析公式为y=kx+b,
但
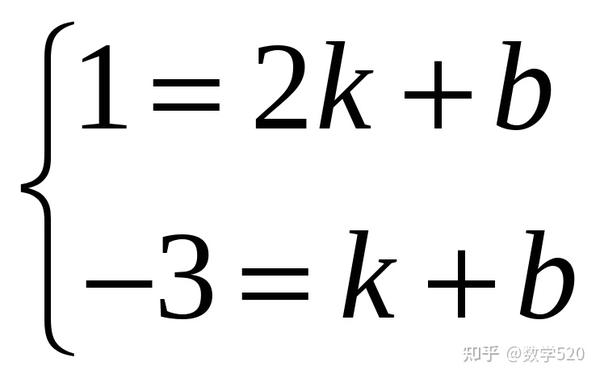
, 解为 k=4, b=-7。
∴y=4x﹣7.当y=0时,x=
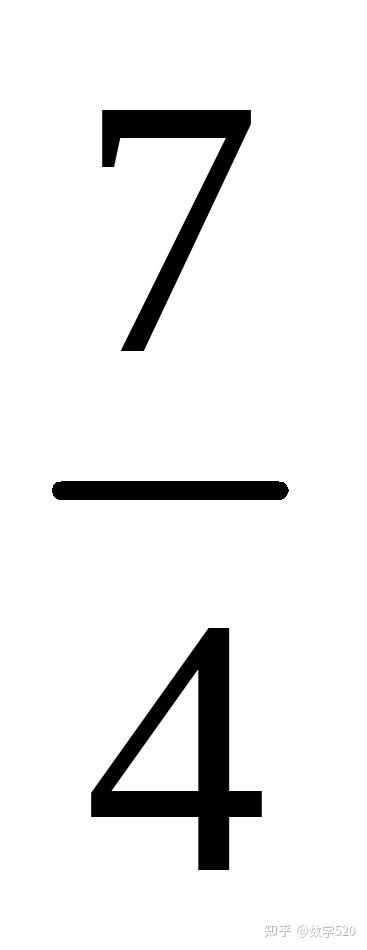
, 即 P(
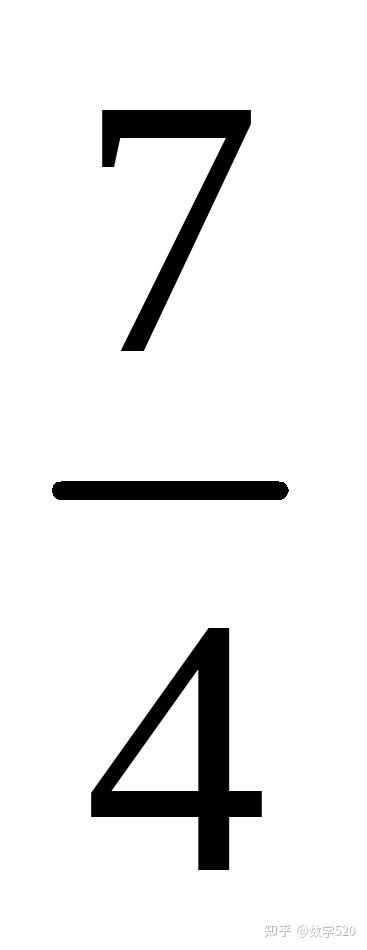
, 0), a=
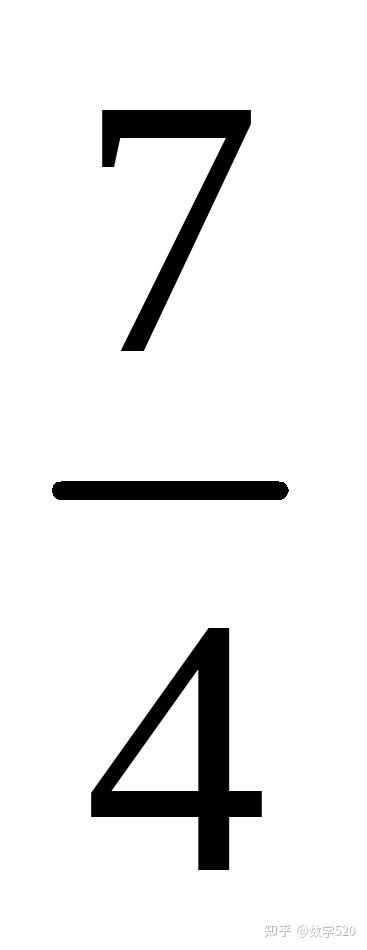
.
所以填写答案:
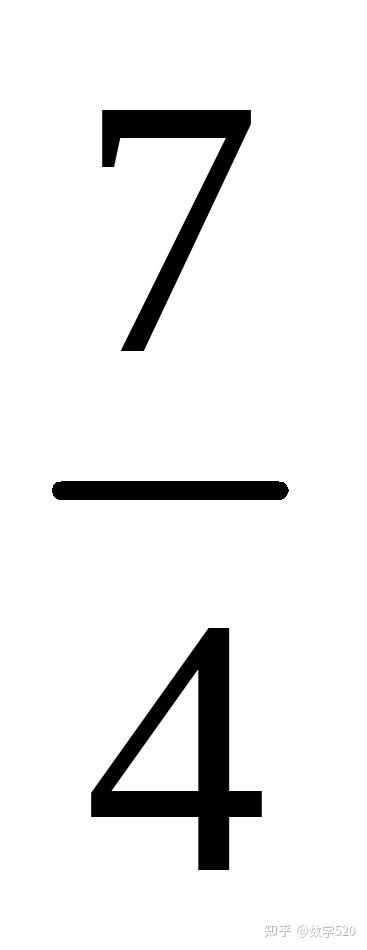
.

【题后思考】检查X轴对称点、两点间最短线段等知识。
3、如图,A、B两点在直线的两侧,A点到直线的距离AM=4,B点到直线的距离BN=1,且MN=4,P为直线上的移动点,|PA﹣PB|的最大值 是 。
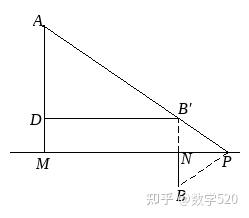
【解析】由于B点放在直线l的对称点B′上,则PB=PB′,因此|PA﹣PB|=|PA﹣PB′|,则当A、B′、P在a直线,|PA -PB| 具有最大的价值。根据平行线段定理可以得到PN和PM的值,然后根据勾股定理可以得到PA和PB'的值,然后|PA-PB的最大值| 可以获得。
【答案】解:在线l的对称点B'上画点B,连接AB',将相交线l延伸到P。
∴B′N=BN=1,
通过点 D 使 B′D⊥AM,
使用勾股定理找出 AB′=5
∴|PA﹣PB|的最大值=5。
【题后思考】本题考查映射——轴对称变换、勾股定理等。知道“两点之间的线段最短”是回答本题的关键。
4、动手操作:在矩形纸ABCD中,AB=3,AD=5。如图,将纸对折,使A点落在BC边上的A'上,折痕为PQ。当 A' 点在 BC 的边缘移动时,折痕的端点 P 和 Q 也会移动。如果限制点 P 和 Q 分别在边 AB 和 AD 上移动,则点 A' 可以在边 BC 上移动的最大距离为 。
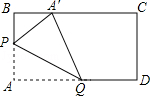
【解析】这个问题的关键在于找到两个极值,即BA'取最大值或最小值时点P或Q的位置。通过实验不难发现,当点P和B重合时,BA'取最大值3,当点Q和D重合时,BA'最小值为1。因此,点 A' 可以在 BC 的边缘移动是 2。
[解答] 解:当点P和B重合时,BA'的最大值为3,
当Q点和D点重合时(如图),由勾股定理得到A'C=4,此时BA'的最小值为1。
那么A'点在BC边上移动的最大距离为3-1=2。
所以答案是:2

【题后思考】本题考察学生的动手能力、图形的折叠、勾股定理的应用。
5、如图,直角梯形纸ABCD,AD⊥AB,AB=8,AD=CD=4,点E和F分别在线段AB和AD上,沿EF折△AEF, A点的落点记为P。当P落在直角梯形ABCD内时,PD的最小值等于 。
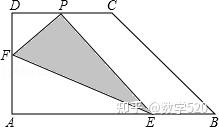
【解析】如图所示,经过分析探索,只有当直径EF最大,且A点落在BD上时,PD才最小;根据勾股定理,可以解出BD的长度,问题就可以解决。
[解答] 解决方法:如图,
∵当点P落在梯形内时,∠P=∠A=90°,
∴四边形PFAE是以EF为直径的圆内接四边形,
∴只有当直径EF最大且A点落在BD上时,PD才最小,
此时,E与B点重合;
从标题:PE=AB=8,
从勾股定理我们得到:
BD2=82+62=80,
∴BD=

,
∴PD=
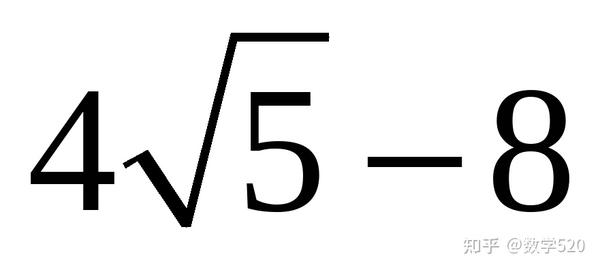
.

【题后思考】本命题以直角梯形为载体等腰三角形知识点及典型习题教案模板3,翻转变换为方法,以考察全等三角形的判断及其性质的应用为核心;解决问题的关键是在运动过程中把握图形的某一时刻,在运动中寻求静止,用静止来刹车。
初中数学要想考到135+,就需要搞懂这些典型的几何题!
- - 结尾 - -
一个温暖的公众号
点亮“看”
让更多人看到
向世界宣布已进12海里