【知识点】三线合一的题型及判定方法汇总!
一、特殊三角形知识点
1、等腰三角形定义、性质、判断。
等腰三角形的性质定理:等腰三角形的两个底角相等(即等边等角)
等腰三角形判断定理:如果一个三角形有两个相等的角,那么这个三角形就是一个等腰三角形
(即等角和等边)
“三线合一”定理:等腰三角形顶角的平分线,底边中线与底边高重合
2、等边三角形
性质:等边三角形内角相等,每个角等于60°
判断:三个角相同的三角形是等边三角形;
三边相等的三角形是等边三角形;

角等于60°的等腰三角形是等边三角形
3、直角三角形
自然:
(1)在直角三角形中,两个锐角互补;
(2)直角三角形斜边上的中线等于斜边的一半;
(3)(补充结论)
在直角三角形中,如果一个锐角等于30°,它所面对的直角边等于斜边的一半;
(4)勾股定理:直角三角形两条直角边的平方和等于斜边的平方;
(5)逆定理:如果三角形三边的长度使得三边的平方和等于第三条边的平方,

那么这个三角形就是直角三角形;
(6)直角三角形全等判断条件HL:斜边和一条直边对应两个相等且全等的直角三角形。
二、问题类型分类
1、关于三行的问题:
(1)等腰三角形的两个底角的角平分线相等;
(2)等腰三角形腰围等高;
(3)等腰三角形腰中线相等;
(4)有角平分线,垂直线,中间两条线是同一条线。想想“三线合一”。
2、Category 讨论问题类型:

(1)没有指定边是底边、腰边、直角边、斜边;
(2)没有强调是底角还是顶角;
例:如果等腰三角形的一个角等于40°,则等腰三角形的顶角的度数是____
在△ABC中,AB=15,AC=13,高AD=12等腰三角形知识点及典型习题教案模板3,那么三角形的周长是
(3)没有强调是锐角还是钝角,需要自己画图;
例题:等腰三角形的顶角为80°,则腰高与底边的夹角为______
(4)没有强调旁边的高线是什么;
例:在等腰线△ABC中,AB=AC=13,一边高5,底边BC长______
(5)keyword "直线,射线"

例:在等腰线△ABC中,AB=AC,AB的垂直平分线与AC所在直线相交所得的锐角
50°,那么∠B=
(6)动点动点问题;
3、Angle 计算或求角的关系:
“三角形的内角和180°”和“三角形的外角等于不相邻的两个内角之和”,“八字模型”,
“同角或等角的余角相等”;
4、求边长或求边的关系:
等角等边、等置换、三角形全等、面积法、截断法、勾股定理、斜中线定理;
5、查找等腰三角形或证明等腰三角形:

两圆一条线,“双平”---平行线+角平分线;
6、手拉手模型(有公共顶点的三角形)
大多数情况下,三角形全等条件是SAS;
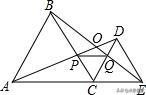
例题:如图,C是线段AE上的一个移动点(与点A和E不重合),在AE、AD的同一边做一个等边三角形ABC和一个等边三角形CDE与BE相交于O点,AD与BC相交 与P点、BE与CD相交,与Q点相交,连接PQ。有以下结论:①AD=BE; ②AB∥DC; ③DP=EQ; ④∠AOE=120°; ⑤PQ∥AE,⑥DE=DP等腰三角形知识点及典型习题教案模板3,其中正确结论是
7、方程思维
如果不能直接求解,让未知数通过一些定理或等价关系建立方程;
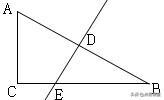
例题:已知在Rt△ACB中,DE为AB的垂线,AC=3,BC=4,则CE=,BE=
我在上面选择了一些常规练习。考虑到习题较多,部分题型不包括样题。如果需要,可以私信我。我希望这些总结对你有帮助。感谢您的关注。
教案网123