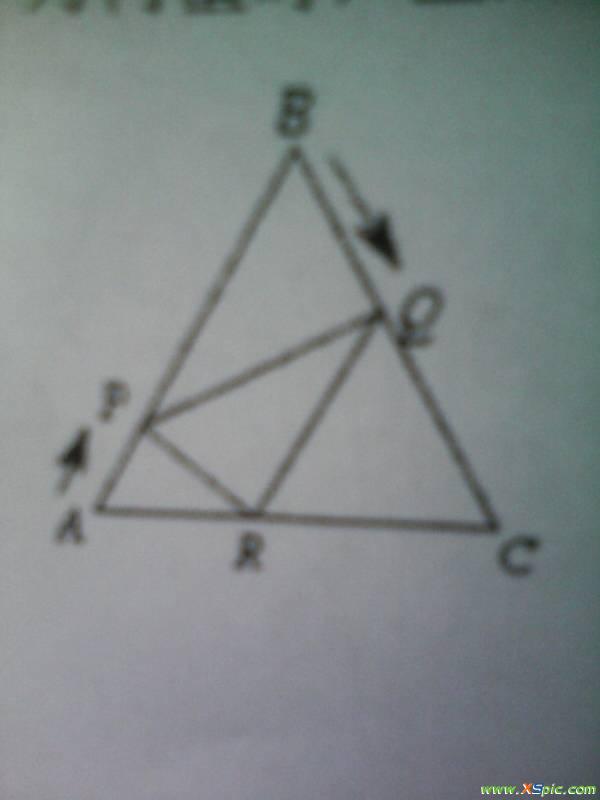
【每日一题】AP与CQ之间的和差关系

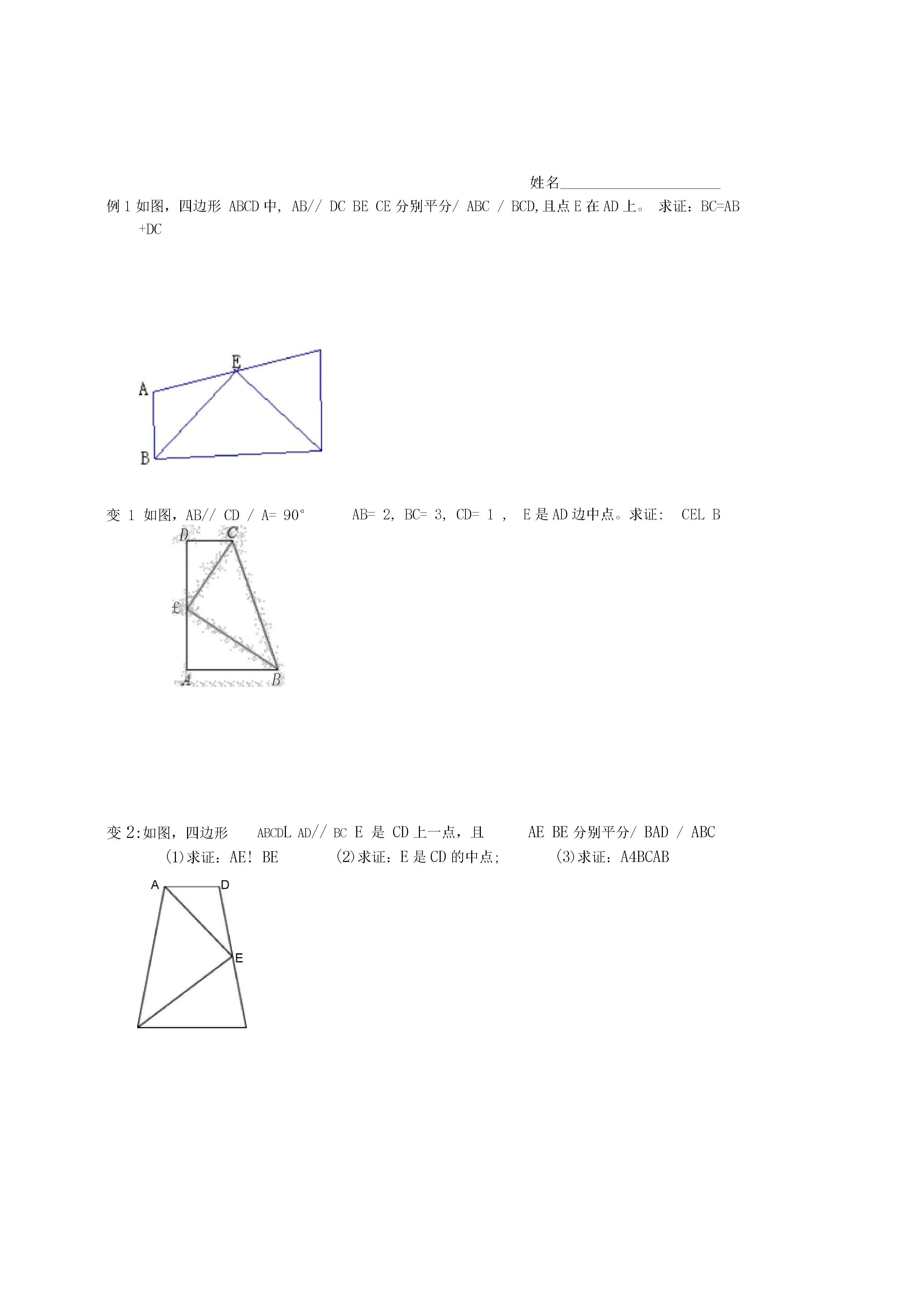
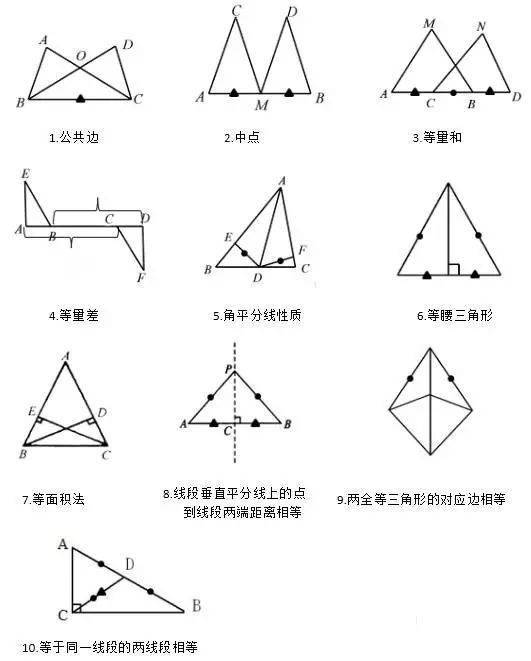
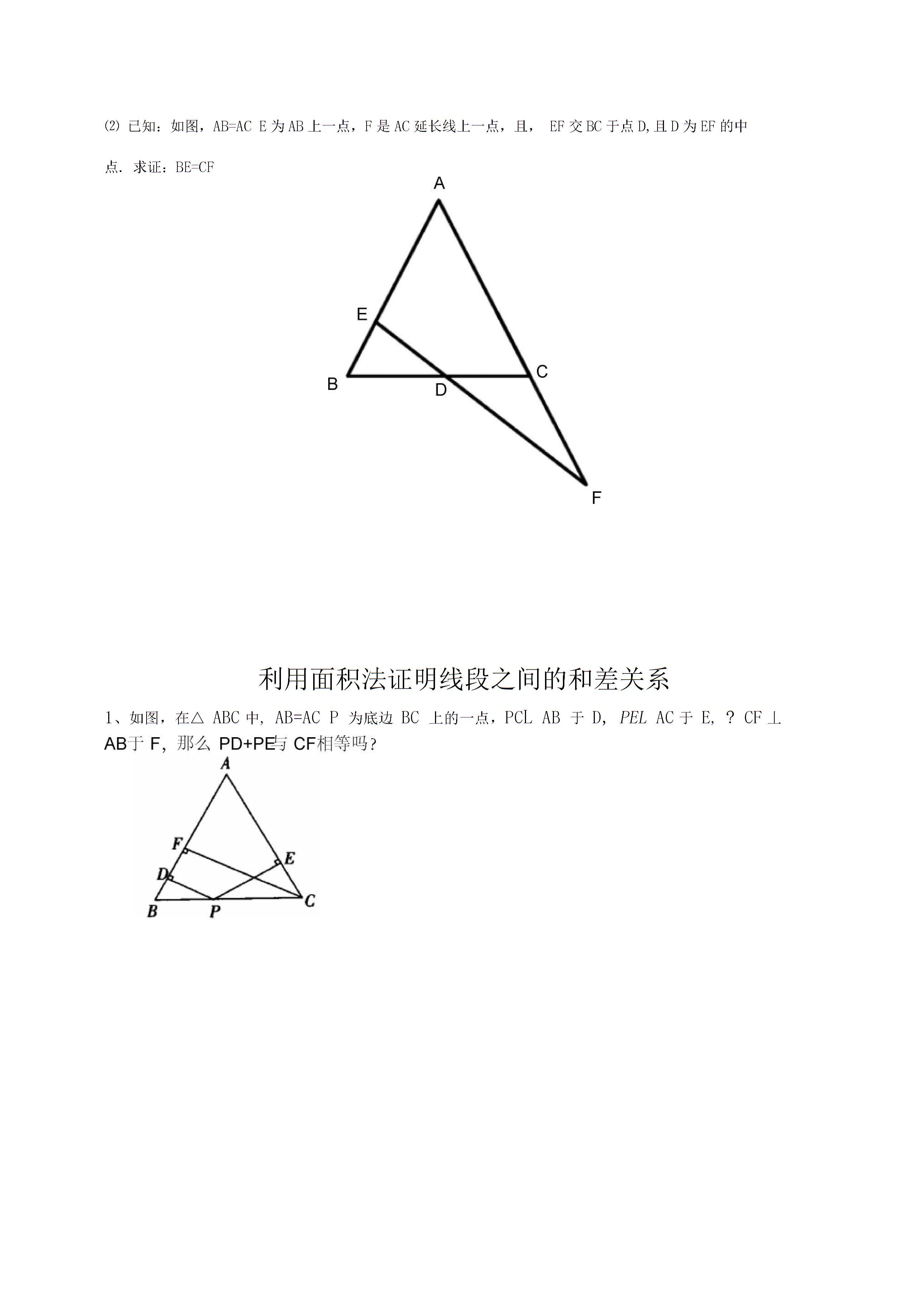
命名例1如四边形ABCD，ABDCBECE等分ABCBCD，在AD上验证点E，BCABDC变为3ABC为等腰直角三角形BAC90ABAC (1) 若D为BC的中点，则通过D使DMLDN 分别到 ABAC 以验证 MN 中的 1DMkDNA。ABACE 是 AB 上的点，F 是 AC 延长线上的一个点，BECFEF 在 D 点与 BC 交叉以验证 DEDF。(2) 如图，ABACE为AB，F点为AC延长线上的一点，EF在D点与BC相交，D为EF的中点。点验证 BECF 使用面积法来证明线段之间的和差关系。1 如图所示，△ABC中的ABACP是BC底边的一个点。PCLAB 和 DPELAC ​​更改为 ECF。PDPE和CF的关系如何，请画图证明1等腰三角形的两条边长分别为49，周长为A17B22C17或22D13。根据等腰三角形的性质求定律。1 例1 △ABC 中的ABAC 核A ABC2ACBBD 与CE 相交于0 点，如图所示。B0C的大小和A的大小有什么关系？11 如果是1ABC2ACB，BOCWZA之间的关系如何？311 如果1ABC2ACB，B0C和ZA nn的关系如何用等腰三角形的判断和性质计算如证明例2所示，等腰三角形ABC中ABAC腰部的中线BD利用等腰三角形的性质三角形证明线段相等。例 3 在等边三角形 ABC 中。将PAPBPC 与BP 连接为PBQ60 和BQBP 与CQ1 连接 观察并猜测AP 与CQ 的大小关系并证明您的结论2 如果PAPBPC345 与PQ 连接，尝试判断△PQC 的形状并解释原因。例1 等腰三角形底边边长为5cm的腰部中线将三角形的周长分成相差3cm的两部分，则腰长为A2cmB8cmC2cm或8cmD，无法确定。例 2 ABC 的高 ABAC 是已知的。ABC的周长是20厘米。如长例3所示，已知BC3ZABC和ACB的平分线在00EABOFAC点相交，求出OEF的周长。例 4 被称为等边 ABC等腰三角形知识点及典型习题教案模板3，其中 D 是 AC 的中点。将 BC 扩展到 E 并将 CECD 连接到 DE。在横线上填写您认为正确的序列号。例8 正三角形ABC所在平面上有一点P，使得△PAB△PBC△PCA都是等腰三角形。A1 B4 C7 D10 例 9 四边形 ABCDKAEBCABZCDA 90°BEAD 在点 E 和四边形 ABC[ 的面积是 8 北 UBEA2B3C22D23P 是它的内点和 AP4BP2

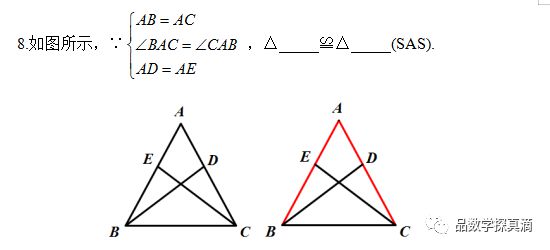
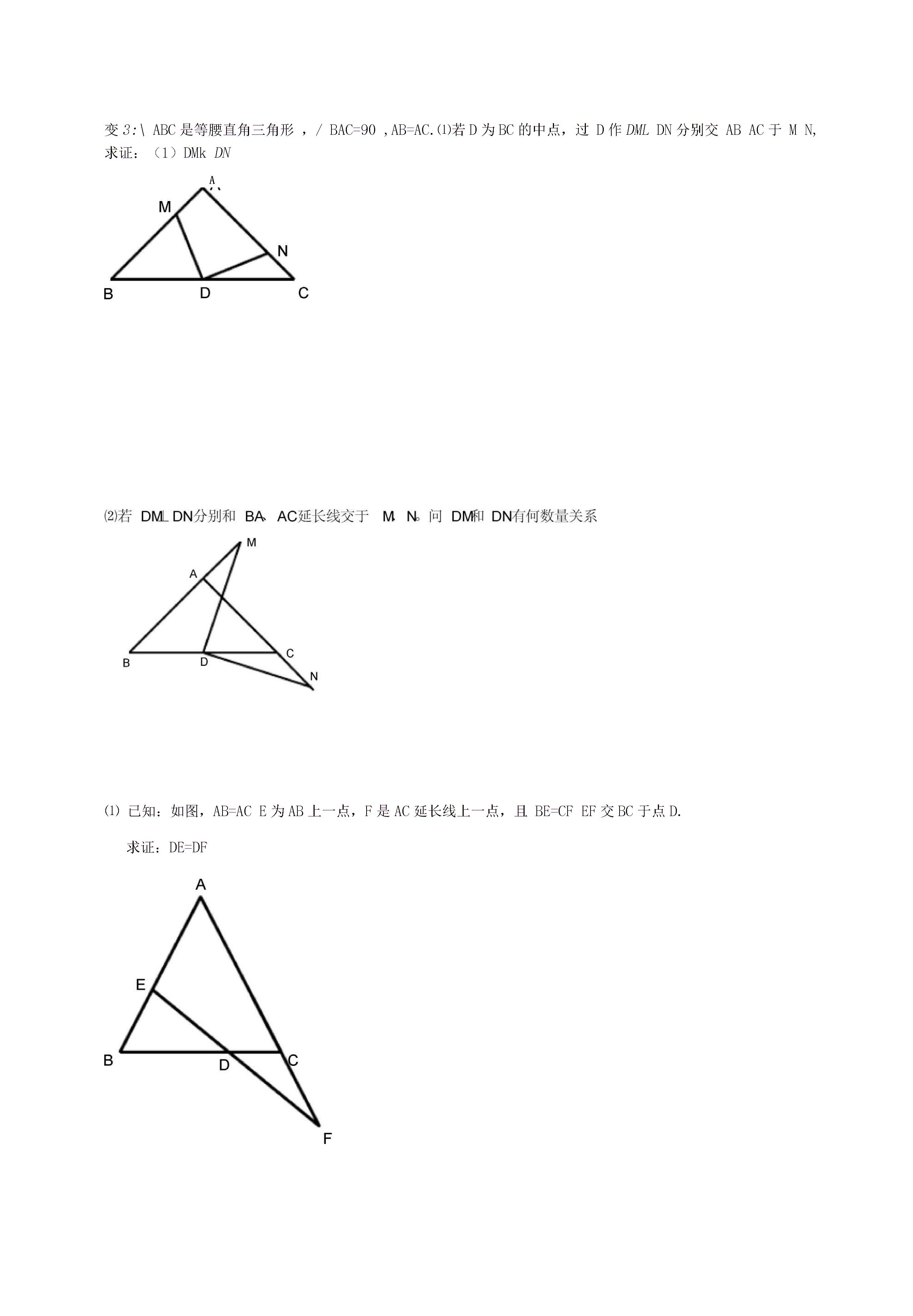
3CP2，ABC的边长是A25B27C4D42 3.巩固练习1 已知等腰三角形的一边等于5，另一边等于9，求它的周长。2 在ABC中，ABACB400为A3等腰三角形，内角为700度，其顶角为4度，内角为40度的等腰三角形的另外两个内角为5度，如Rt△ABC所示， 8105°直线BD在D处与AC相交，直角三角形沿直线BD转。C点恰好落在斜边AB上。欢迎下载合同下载合同模板下载红头文件模板免费下载简历免费下载模板工作简历模板免费下载如果△ABD是等腰三角形则A等于A40°B300C25°D15°bc且满足a2b2c2506a8b10c直角三角形如图所示的C等腰直角三角形13，除框架AC上的端点AC外，为等边三角形木架甲虫P。设甲虫P与另外两侧的距离之和为d。等边三角形ABC的高是h，那么d和h的大小关系是解题，乘法，口算，100题，七年级，有理数的混合运算，100题，计算机先行-级题库，二元线性方程，应用题，真相或冒险，刺激问题方法指导例1 ABACCD验证B2D例2 △ABC 是等边三角形ADBCAD和BDBC6。AD 的长测试点是指等腰三角形。等边三角形和30°角的直角三角形是使用非常广泛的图形。因此，中学试题中的50套危险化学品试题是安全的。资格证书考试题银行机构招聘面试卡特尔16pf性格测试经常作为证明题或计算题出现，并经常将它们组合在一个问题中。题型虽然难度不是很大，但要善于分析和找图。相关属性典型实例分析 实例1 2005年，苏州等腰三角形ABC的顶角为120°，腰长为10，则底边的高AD。AB 和 E 在 DAD8A30°处与 AC 相交以找到 CD。3 已知如图△ABC为等边三角形，E为AB上的点，D为AC上的点，AECD与BD与CE相交于F点。试求BFE的度综合测试已知如 ABACABDZACD 中所示以验证 DBDC6。如△ABC所示，B90°AC的垂直平分线在D处与AC相交，在E和C15°EC处与BC相交。对于分别在 ABAC 和 DEXDF 上的 BC 边 EF 的中点，findCertificate AEAF 是一个固定值证书，连接 AD•ABACD 作为 BC•••AD-BC•••BAC90°ABACBZC45°•••BAD45°CAD45°•ADBDCD•••EDF90°EDAZADF90°和来自 ADLBC 的 ZBDEZADE90° BDEDADF中的BDEZADF ZBZDAFBDADZBDEZADF•△BDEAADF•BEAF•AEAFAEBEAB定值想想四边形AEDF的面积是否也是定值？为什么示例4 如图9 所示，已知ADABC 的高E 是AC 上BE 穿过AD 到F 的点，存在BFACFDCD。你认为BE和AC之间有什么样的位置关系。你能证明这个吗？证明线段BEAC的理由如下： •AD丄BC•••ADBZADC90°•ZFBDZBFD90°BFACF»CD•••Rt△在Rt△BDF和Rt△ADC BDFRt△ADC••••BFDZC「FBDZC90 °•••BEC180°-ZFBDZC180°90°90°即BEXAC22示例5 如图10所示，

BCCD-AB•AZB45°ACDZBCD45•••AACDBBCD•ADBDBDCD是ADBDCD•••CD-AB•DM2CD2CM2•AM2BM2AD-DM2BDDM22DM2CD22CMCD2CF•CFDF在CEF和DEF如图CFDFCFEDFE90FEFDE在△BC上的任意一点， ,PD,AB 在点 DPELAC ​​在点 E，验证 PDPE 是一个固定值，本例的结论可以用文本语言描述为等腰三角形底边上的一点到两个腰部的距离。通过将 AP 连接到 C 点作为 F 点的 CFLAB 来解决和等于腰高之间的关系，如图 811 中 SABC2ABCFSpab2ABPD11SPACACPEABPE22 所示。基本训练 1 填空等腰三角形。如果底长是6，腰长是8，那么周长是如果等腰三角形的一边长是6，另一边长是8，那么它的周长是如果等腰三角形的两条边都是48，那么它的周长就是等腰三角形的对称轴。最多有 2 个填空。ABC是一个等腰三角形，所以它的边长或周长可以是A，三边长是5511B，三边是448C等腰三角形知识点及典型习题教案模板3，周长是14，两边是45D，周长是24，两边是612等腰。三角形的一条边长为2，周长为5，所以它的腰长是A3B2C15D2或153。知道等腰三角形的腰长是底边的3倍，周长是35cm。求等腰三角形各边的长度。4 已知如图AD 划分BACABAC，请说明DBC 是一个等腰三角形x2y43xy75。知道等腰三角形的底边和长度是方程的解来找到这个三角形的边。等腰三角形顶角的平分线彼此重合。一个角为120°，则其他两个角的度数与△ABC中的AZB2C相同，然后等腰三角形中的C，设底角为x，顶角为y，然后使用包含x的代数表达式表达 y 得到 y 数来表达 x 到 x2。等腰三角形的外角为140°，则底角等于A40°B100°C70°D40°或70°等腰三角形的高线与底边的夹角等于其顶角A，B的底角，C的顶角。在等腰三角形ABC中，A与B的度数之比为52，那么A的度数是A100°B75°C150°D75°或100°ABC 其中ABACAD是角的平分线，那么①AD∄BC②BDDC④BADCAD的正确结论数是3C2DABC，D在BC上，ABADDC4称为△ ABC 中点 DE 在 BC ABACADAE 请解释 BDCE 勺子的原因 1 填空题 1 ABC 中 A 的相邻外角为 110°。若△ABC为等腰三角形，则B2等于三角形的等边角。如果等腰三角形底边的高线与腰部的高线相等，则每个内角的度数为4，如ABABCBD和ABC等分。在C2ZA中，图中的等腰三角形共有2道选择题。如△ABC所示，ABACBAC108ADB72DE平分ADB。那么图中等腰三角形的个数为A3B。在ABC中，B 和 C 的平分线相交于点 0 和 0B0C。请解释ABACf原因4如图所示。EACABC 的外角是已知的。图 5 显示在 ABACABDACD 中。请解释为什么 AD 是 BC 的垂线 ABAC。