教师招聘考试备考：向心加速度公式推导与应用

向心加速度【教材分析】1．匀速圆周运动的加速度方向； 2．向心加速度的大小。【教学目标】1．理解向心加速度的概念。 2．知道向心加速度和线速率、角速度的关系式。 3．能够利用向心加速度公式求解有关问题。【核心能力】物理思想：建立向心加速度的方向跟大小的方式微元法的数学思想。 科学认知：培养教师思维能力和预测问题的素养，培养教师研究问题的热情，乐于 学习的品质。 科学研究：体验向心加速度的导出过程，领会推导过程中用到的物理方式。 科学态度与责任：通过向心加速度的方向及推导的学习，培养教师了解未知世界要 有善于猜想的胆量和细致的科学态度。【教学重点】1．理解匀速圆周运动中加速度的产生因素，掌握向心加速度的确认方式跟计算公 式。 2．向心加速度方向的确认过程跟向心加速度公式的计算与应用。【教学难点】向心加速度方向的确认过程跟向心加速度公式的计算与应用【教学过程】教学环节教师活动学生活动设计动机导入新课 做曲线运动的物体速度必定是差异的，因此 回忆做曲线 为引出本节课做曲线运动的物体，一定有加速度，圆周运 运动的物体 题做圆周运动动是曲线运动，那么做圆周运动的质点，加 速度一定是 的物体，加速速率的大小跟方向怎样确认呢？变化的，因 度的大小跟方——这就是我们最近要研究的课题。

此一定存在 向做铺垫。加速度。1/11讲授新课 一、匀速圆周运动的向心加速度及其方向1．向心加速度的方向：总是指向圆心，方向时刻改变，方向总是与速率方向平行。物体做匀速圆周运动时，合力的方向总是指向圆心，根据牛顿第二定律，物体运动的加速度方向与它所受合力的方向同样，即：物体做匀速圆周运动时的加速度总指向 观察图片说 理解向心加速圆心。出向心加速 度的方向。度的方向。物体做匀速圆周运动时，合力的方向总是指向圆心，根据牛顿第二定律，物体运动的加速度方向与它所受合力的方向同样，即：物体做匀速圆周运动时的加速度总指向圆心。2．向心加速度：任何做匀速圆周运动的质点的加速度都指向圆心，这个加速度叫做向心加速度。3．向心加速度的作用只改变速率的方向，对速度的大小无妨碍。注意：无论 an 的大小是否变化，其方 向时刻改变，所以圆周运动的加速度时刻发 生变化，圆周运动是变加速曲线运动思考讨论 1：变速圆周运动的加速度和 向心加速度有哪些关系？学生探讨讨 论理解做变速圆 周运动的物 体，加速度并 不指向圆心， 切向加速度改变速率的大小。2/11做变速圆周运动的质点，加速度并不指向圆心，该加速度有两个分量：一是向心加速度；二是切向加速度，切向加速度改变速率的大小。

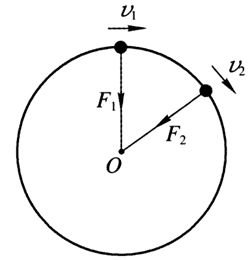
因此通常状况下，物体做圆周运动的加速度方向不必定指向圆心。思考争论 2：匀速圆周运动的加速度和 学生反思讨 理解匀速圆周向心加速度有什么关系？匀速圆周运动是否 论问题 2 运动加速度和为匀变速运动？向心加速度相匀速圆周运动的加速度和向心加速度含同，方向时刻义相似。由于匀速圆周运动的加速度始终指在改变向圆心，其大小不变，但方向时刻在改变，所以匀速圆周运动不是匀变速运动。思考讨论 3：向心加速度与合加速度之 学生探讨讨 理解向心加速间有哪些关系？论难题 3 度与合加速度对于匀速圆周运动而言，物体的加速度之间的关系。即为向心加速度，因此其方向必定指向圆心；物体做变速圆周运动时，合加速度必有一个沿切线方向的分量和指向圆心方向的分量，其对准圆心方向的分量就是向心加速度。对于非匀速圆周运动，沿切线方向的加速度改变线速率的大小。4．向心加速度的物理含义思考探讨：向心加速度是从那个角度描 思考探讨向 理解向心加速述速度差异快慢的？说明原因？心加速度的 度是描述速度由于向心加速度的方向总指向圆心，与 物理意义 方向改变快慢速度方向平行，所以向心加速度只改变速率的物理量。方向，不改变速率大小，因此向心加速度是描述速度方向改变快慢的物理量，向心加速度大，即速度方向改变得快。

二、向心加速度的大小1．向心加速度表达式思考讨论：由向心力的表达式，你可推3/11导出向心加速度表达式吗？由向心力：Fn=mv2 R或Fn=mrω2根据牛顿第二定律 F＝ma，得an=v2 r或an=rω2学生由向心 锻炼学生的推 力的表达式 导能力 推导出向心 加速度表达 式注意：向心加速度的定理适用于任何圆周运动。2．向心加速度的各种表达式由匀速圆周运动向心加速度的基本定理，结合各物理量间的关系，你能计算出匀速圆周运动向心加速度的几种表达方式？由 an=rω2v2 an= rv=ωr推导出向心 加速度的各 种表达式。锻炼学生的逻 辑思维能力。ω=2π/T=2πf=2πn 得an=vω2? an=（ T）2ran=（2πf）2ran=（2πn）2r 思考与探讨：从推导 an＝v2/r 看，线速 度一定时，向心加速度与圆周运动的边长成 反比；从公式 an＝ω2r 看，角速率一定时， 向心加速度与长度成正比。学生探讨与 讨论理解推导 an＝v2/r 和 an＝ω2r 的含 义。自行车的大齿轮、小轴承、后轮的直径不一样，它们的边沿有三个点 A、B、C，如图所示。其中那两点向心加速度的关系适用于“向心加速度与长度成正比”，哪两点适用于“向心加速度与半径成反比”？给出解释。

B、C 两点在同一轮上，同轴传动时，4/11这两点的角速度相等，由定理an＝ω2r 知 ω 一定时，向心加速度与半 径成正比。A、B 两点在同一个链条上，两点的线速率大小相等，由 an＝v2/r 知 v 一定时，向 心加速度与半径成反比。【例题】如图所示，在长为 l 的绳子下端拴一个质量为 m 的小球，捏住细绳的下端，使小球在水平面内做圆周运动，细绳就沿圆锥面旋转，这样就成了一个圆锥摆。当绳子和竖直方向的倾角为 θ 时，小球运动的向心加速度 an 的大小为多少？ 通过计算表明：要减少夹角 θ，应该减小小球运动的角速率 ω。锻炼学生的分在老师的引 析计算能力导下预测计算分析因为小球在水平面内做圆周运动， 向心加速度的方向一直指向圆心。可以按照 受力分析，求出向心力的大小，进而求出向 心加速率的大小。根据向心加速度公式，分 析小球做圆周运动的角速率 ω 与夹角 θ 之间 的关系。解：根据对小球的受力分析，可得小球 的向心力 Fn＝mgtanθ根据牛顿第二定律可得小球运动的向心 加速度：an＝Fn/m＝gtanθ（1） 根据几何关系推测小球做圆周运动的半 径 r＝lsinθ（2）5/11把向心加速度公式 an＝ω2r 和（2）式代 入（1）式，可得 cosθ＝g/lω2从此式可以看出，当小球运动的角速率减小时，夹角也逐渐减少。

因此，要减少夹锻炼学生的自角 θ，应该减小小球运动的角速率 ω。主学习能力，拓展学习演算向心加速度公式学生阅读课 体验向心加速用运动学的方式求做匀速圆周运动物体 文度的导出过的向心加速度的方向与大小。理解用运动 程加速度教案模板，领会推导1．向心加速度的方向学的方式求 过程中用到的做匀速圆周 数学方式。运动物体的向心加速度（1）一质点沿着圆周运动，在 A、B 两点的速度分别为 vA、vB，画出物体经过 A、B 两点时的速度方向。的方向与大 小。（2）平移 vA 至 B 点，根据矢量运算法 则，做出物体由 A 点至 B 点的速率差异量Δv。由于质点做匀速圆周运动，vA、vB 的大 小相等，所以，Δv 与 vA、vB 构成等腰三角 形。（3）假设由 A 点至 B 点的时间慢慢减 小直至极短，在匀速圆周运动的速率大小一 定的状况下加速度教案模板，A 点到 B 点的距离将更加小， 作出此时的 Δv。6/11Δv 逐渐趋于于平行 OA A 点至 B 点的时间极短时，Δv 与 vA、 vB 都几乎垂直，因此 Δv 的方向几乎沿着圆 周的直径，指向圆心。由于加速度 a 与 Δv 的方向是一致的，所以从运动学角度探讨也 可以看到：物体做匀速圆周运动时的加速度 指向圆心。

2．向心加速度的大小计算向心加速度公式 由图可知，当 Δt 足够小时，vA、vB 的 夹角 θ 就足够小，θ 角所对的弦和弧的宽度 就近似相同。因此，θ＝v\Δv，在 Δt 时间 内，速度方向变化的视角 θ＝ωΔt。由此能 以求得： Δv＝vωΔt 将此型代入加速度定义式 a＝Δv\Δt，并 把 v＝ωr 代入，可以读入向心加速度大小的 表达式为 an＝ω2r7/11巩固本节知识上式也可以写成 an＝v2/r学生练习它与依据牛顿第二定律得到的结果是一致的。课堂练习1．质量相同的 A、B 两物体分别做匀速圆周运动，若在相同的时间内通过的弧长之比为 2：3，而转过角度之比为 3：2，则A、B 两质点周期之比为——————，向心加 速度之比为——————。答案：2：3；1：12．一物体在水平面内沿直径 R=20cm的方形轨道做匀速圆周运动，线速率v=0.2m/s，那么，它的向心加速度为0.2m/s2，它的角速度为_______rad/s，它的周期为_______s。答案：1；2π3．关于向心加速度的表述正确的是（）A．向心加速度越大，物体速度变化越快B．向心加速度的大小与轨道长度成反比C．向心加速度的方向一直与速率方向平行D．在匀速圆周运动中向心加速度是恒量答案：C4．A、B 两艘船只在水面上做匀速圆周运动（如图），在同样的时间内，它们借助的路程之比是 4：3，运动方向改变的视角之比是 3：2，则他们（）A．线速度大小之比为 3：4 B．角速度大小之比为 3：4 C．圆周运动的长度之比为 8：98/11D．向心加速度大小之比为 1：2 答案：C 5．转笔是一项备受广大青少年喜爱的 休闲活动，其中也包括了许多的物理知识。

假设某同学将笔套套在笔头的一端，在转笔 时使笔头绕其双手上的某一点 O 在竖直平 面内做匀速圆周运动，则以下描述中恰当的 是（） A．笔套做圆周运动的向心力是由笔杆对其 的摩擦力提供的 B．笔杆上离 O 点越近的点，做圆周运动的 向心加速度越大 C．当笔杆快速转动时笔套有也许被甩走 D．由于匀速旋转，笔套受到的摩擦力大小 不变 答案：C 拓展提高 1．两架飞机在空中沿水平面上做匀速 圆周运动，在同样的时间内，它们借助的路 径之比为 2：3，运动方向改变的视角之比 为 4：3．它们的向心加速度之比为多少 （） A．2：3 B．8：9 C．2：1 D．1：2 答案：B 2．如图所示皮带传动轮，大轮直径是 小轮直径的 3 倍，A 是大轮边缘上一点，B 是小轮边缘上一点，C 是大轮上一点，C 到 圆心 O 的距离等于小轮半径，转动时皮带 不打滑。则 A、B、C 三点的角速度大小之 比，线速率大小之比，向心加速度大小之比9/11分别为（）A．ωA：ωB：ωC=1：3：3 B．vA：vB：vC=3：3：1 C．aA：aB：aC=3：6：1 D．aA：aB：aC=1：9：3 答案：B3．下列关于匀速圆周运动的表述中，正确的是（）A．因为向心加速度大小不变，故是匀变速运动B．由于向心加速度的方向差异，故是变加速运动C．用线系着的物体在光滑水平面上做匀速圆周运动，线断后。

物体受到离心力作用，而背离圆心运动D．向心力和离心力一定是一对作用力和反作用力答案：B课堂小结1．做匀速圆周运动的质点，其向心加 梳理自己本 根据学生表速度的方向沿直径指向圆心，方向时刻变 节所学知识 述，查漏补化，匀速圆周运动为变加速曲线运动。进行交流 缺，并有对于2．向心加速度只改变做圆周运动的物性地进行讲解体的速率方向，而切向加速度改变做圆周运补充。动的物体的速率大小。v2 an= ran=rω22? an=（ T）2ran=（2πf）2r3．向心加速度意义：描述速度方向差异 的强弱的物理量。10/11板书一、匀速圆周运动的向心加速度及其方向1．方向：总指向圆心，方向时刻改变，方向总是与速度方向平行。2．向心加速度：任何做匀速圆周运动的质点的加速度都指向圆心，这个加速度叫做向心加速度。3．物理含义：向心加速度是表述速度方向改变快慢的物理量。二、向心加速度的大小v2 an= ran=rω22? an=（ T）2ran=（2πf）2r11/11