【教师招聘】向心加速度教学设计课题-乐题库

向心加速度》 向心加速度》教学设计课题向心加速度课时1 课时课型新培训1．教材在教师的原有加速度概念的基础上来讨论“匀速圆周运动速率差异快慢”的弊端， 让学生知道向心加速度能够表示匀速圆周运动物体速度差异的强弱究竟是如何一回事。 2．教材把向心加速度安排在线速度跟角速率知识以后，使学生对叙述匀速圆周运动的几 教材 分析 个物理量有一个大致的知道。 3．教材从认识运动的规律过渡到认识力跟运动关系的规律；把向心加速度放在向心力之 前，从运动学的视角来学习向心加速度。 4．教材为了培养教师“用事实说话”的“态度”，让一切阐释都合乎逻辑，改变了过去 从向心力推导向心加速度的教学方法。 1．采用理论、实验、体验相结合的课堂安排。 教学 方法 2．教师启发引导，学生自主阅读、思考，讨论、交流。 1．会作矢量图表示速率的差异量与速度之间的关系。 2．加深理解加速度与速率、速度差异量的差别。 3．体会匀速圆周运动向心加速度方向的预测步骤。 4．知道向心加速度的定理也适用于变速圆周运动；知道变速圆周运动的向心加 速度的方向。 5．知道向心加速度的概念；知道向心加速度的大小与这些原因有关。 6．知道公式ɑ=υ2/r=ω2r 的意义。

7．会应用向心加速度定量分析有关现象。 过程 与方 法 体会速度差异量的处理特性，体验向心加速度的导入过程，领会推导过程中用到 的物理观念。知 识 与 教学 目标 技 能情 感 态 度 与 价 值观 重点 理解匀速圆周运动中加速度的产生因素，掌握向心加速度的确认方式跟计算公 式。 向心加速度方向的确认过程跟向心加速度公式的推论与应用。 教学过程设计 教师活动 学生活动 学生活动 培养教师思维能力和预测问题的素养，培养教师研究问题的质量。教学 重难 点难点1．播放视频欣赏：2009 年 2 月 22 日进行的大冬会花样滑 1．仔细观察后回答：张丹、 冰双人滑赛事毫无悬念，我国大将张丹、张昊以 195．32 张昊的运动做圆周运动。 分获得亚军，在家门口收获了人们的大冬会三连冠。 2．认真听同学讲解，并联系 2．提出疑问：视频中张丹、张昊的运动做哪些运动？ 实际积极探讨。3．许多科学看到都来源于对生活现象的细致观察和仔细 3．认真反思，讨论、交流后， 思考。我们要学习如何从普通的现象中看到问题，提出问 积极发表看法。 题。 下面就请你们看两个视频。 请同学们注意观察并探讨， 你从中有什么发现或疑问？ ①由于惯性， 球离手后失去手 的拉力， 将维持原有运动状况 4．展示视频 1──链球的运动；视频 2──播放一段汽车 不变。

所以飞出时沿切线。 拐弯的视频。 引入 新课 ②球离手后靠重力做抛体运 5．根据学生已有的背景知识，提出以下问题： 动。球离手后也受力，做的是 斜抛运动， 离手前则做圆周运 ①为什么链球离手后会沿直线（切线）飞出，运动员如何 动。 可见手的拉力与圆周运动 控制它飞出的方向？ ②离手后球不受任何力的作用吗？ ③汽车转弯处道路应做成倾斜的？路面倾斜直接妨碍到 什么力？转弯则说明了什么样的运动状况？ ③转弯是曲线运动 （其他学生 补充：在这里就是圆周运动， 使支持力的方向不 6．教师在每个问题强调后立即组织同学们做详细的剖析 不是平抛） 和讨论。 再是竖直向下的，说明支持力 的方向与圆周运动有关； 而且 7．总结归纳：其实这种弊端归根到底都是做圆周运动的 转得越厉害加速度教案模板，坡度就越大。 物体的受力问题！我们了解圆周运动也有曲线运动，曲线 之间有关联。链球转得越快， 人就越站立不稳。 可见手的拉 力大小与圆周运动的强弱有 关。运动的条件？──力与速度不在一条直线上，这样力能够 改变物体运动的方向。但链球出手后在重力作用下，做的 是抛物线运动，而离手前能够做圆周运动，可见圆周运动 物体的受力与抛体受力也有不同的地方。

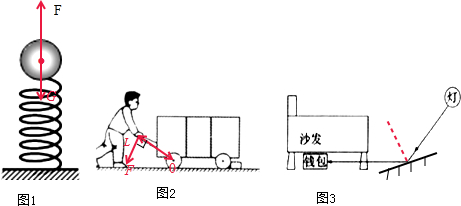
本节课要探究的 是质点做匀速圆周运动时的加速度，了解物体的受力状况 有助于加速度问题的缓解。 8．我们将要知道，作曲线运动的物体，速度必定是差异 的，一定有加速度。圆周运动是曲线运动，那么做圆周运 动的物体，加速度的大小跟方向怎样来确定呢？下面我们 共同来分析这个难题。 1．投影图 5．6－1 和图 5．6－2 以及对应的问题。 1．认真观看交流后回答：图 图 2 中地球遭到什么力的作用？这个力可能沿什么 1 中宇宙受到指向太阳的引力 方向？图 2 中小球受到几个力的作用？这几个力的 作用。图 2 中小球受到重力、 合力沿什么方向？ 支持力跟绳子的拉力三个力 的作用， 其合力即为绳子的拉 3．提出难题：我们这节课要探究的是匀速圆周运动 力，方向指向圆心。 的加速度， 上面两个例题却在探究物体所受的力， 为 什么呢？ 感 知 加 进行新 速 课 度 的 方 向 2．根据牛顿第二定律可知， 知道了物体所受的合外力， 就 4．指导学生用细线和小球做实验。分组用细线拉小 可以知道物体的加速度， 这样 钢球、 小木球让其做匀速圆周运动， 改变小球的转速、 就可以借助力来研究加速度 细线的宽度多做几次。

吧。牛顿第二定律告诉我们， 物体的加速度方向总是和它 这个关系不 5．提出疑问：是不是由此可以得出结论：“任何物 的受力方向一致， 体做匀速圆周运动的加速度都指向圆心”？ 仅对直线运动正确， 对曲线运 动也相同正确。 所以先借助研 6．指出：暂时不能，因为里面只研究了有限的例子， 究力来认知加速度， 特别是加 还无法得出一般性的推论。然而这种的探究十分有 速度的方向。 益， 因为它强烈地向我们提醒了疑问的答案， 给我们 指出了方向， 但是我们确切研究时却应从加速度的定 3．在学生的指导下做实验。 在实验中， 充分认知做匀速圆 义来进行（ ）。下面我们将对圆周运动的加 周运动的物体所受的力或合 外力指向圆心， 所以物体的加 速度也指向圆心。速度方向作一般性的探讨。1．出示例题：向东做加速运动，初速度 5m/s，末速 1．分组讨论认真反思后在练 度 8m/s ，试画出速度的改变量。某物体向东做减速 习本上画出物体加速运动和 运动，初速度 8m/s，末速度 5m/s，试画出速度的改 减速运动时速度差异量的图 变量。 示并提问问题。2．引导学生在练习本上画出物体加速运动跟减速运 2．在老师的引导下画出初速 动时流速变化量Δv 的下图。

第一步： 分别在 A 点跟 B 点做出速度矢量 VA 和 VB， 由于是匀速圆周运动，VA 和 VB 的长度是一样的。 速 度 的 变 化 量 3．问：速度的差异量是矢量还是标量？从以上两例 我们了解速度改变量可以如何画法？如果初速度 V1 和末速度 V2 不在同一直线上，如何表示速率的差异 量Δv？ 4． 引导学生探讨并在黑板上板演画出初速度 V1 和末 速度 V2 不在同一直线上的差异量Δv。 5．投影学生所画的下图，点评、总结。 6．倾听学生提问，启发和鼓励学员解决疑难，总结 并点评。同时引发下一课题。 第三步：在图上画出速度改变量△v。 第二步：将 VA 的起点移至 VB 的起点；末速度 V2 不在同一直线上的差异量Δv。 度 V1 和末速度 V2 不在同经常 线上的差异量Δv。指导教师阅读课本“向心加速度”部分，投影图 5．6 1． 按照老师提出的探讨问题， －3，引导学生反思：①在 A、B 两点画速度矢量 VA 认真阅读课本， 思考问题并回 和 VB 时，要留意什么？②VA 将的起点移至 VB 点时 答。 要切记什么？③如何画出质点由 A 点运动到 B 点时 速度的差异量Δv？④Δv／Δt 表示的含义是哪个？ 2．阅读课本“做一做”栏目 ⑤Δv 与圆的长度平行吗？在哪个条件下，Δv 与圆 中的内容跟朋友一起讨论并 的半径平行？ 在练习本上计算向心加速度 的推导。

（在教师的指导下分 倾听学生提问，必要时给学是以有益的启发和帮助， 为 5 步） 引导学生缓解疑难，回答学生或许提出的疑问。 ①分别做出质点在 A、B 两点 3．指导教师阅读课本“做一做”栏目，要求学生分 的速率矢量（长度一样）。 小组探讨后在练习本上计算向心加速度的定理。 ②将 VA 的起点移至 B，并保 4．巡视学生的计算情况，解决学生推导过程中或许 持 VA 的长度跟方向不变。 遇到的困难，给与帮助，回答学生或许提出的难题。 ③以 VA 的箭头端为起点，VB 5．．师生互动，共同这样来计算向心加速度的推导。 的箭头端为终点作矢量Δv。 向 心 加 速 度 图1 如图 1 所示， 做匀速圆周运动的质点的线速率大小为 v，角速率为ω，轨迹宽度为 r。物体从 A 点运动至 3．引导学生反思并完成“思 B 点，经历时间 t，位移为 S。可以将位移分解为沿 考与探讨”栏目中强调的问 切线方向的位移 S1 和沿长度方向的位移 S2。当时间 题。深化本节课所学的内容。 t 很小更小时，可以觉得物体在切线方向做匀速直线 运动，在直径方向做初速度为 0 的匀加速直线运动， 加速度为 a，即 S1=vt 于是 ⑤当Δt 很小更小时，AB 非 常接近， 等腰三角形的底角接 （或 近直角， Δv 的方向和 VA VB） 的方向垂直。

即指向圆心。 ④Δv/Δt 是质点由 A 到 B 的 平均加速度， Δv 的方向就 是加速度的方向。其方向沿长度方向，即为向心加速度。投影学生计算的过程，和学生一起点评、总结。 指出：上面的计算不涉及“地球公转”、“小球绕图 钉转动”等详细的运动，结论带有一般性：作匀速圆 周运动的质点加速度指向圆心。 这个加速度称为向心 加速度。例：如图所示，一个大轮通过皮带拉着小轮转动，皮带和四轮之间无相对滑动，大 轮的半径是小轮半径的 2 倍，大轮上的一点 S 离旋转轴的距离是直径的 1/3。当大 轮边缘上的 P 点的向心加速度是 0．12m/S2 时，大轮上的 S 点跟小轮边缘上的 Q 点 的向心加速度各为很大？解析： 解析：P 点跟 S 点在同一个转动车轮上，其角速率相同，即ωp＝ωs．由向心加速度 公式 a＝rω2 可知：as/ap＝rs/rp， ∴as＝rs/rp·ap＝1/3×0．12m/s2＝0．04m/s2。典型例题由于皮带传动时不漏油，Q 点跟 P 点都在由皮带传动的两个轮子边缘加速度教案模板，这两点的线 速度的大小相同，即 VQ＝VP。由向心加速度公式 a＝v2/r 可知：аQ/аP＝rP/rQ，∴ aQ＝rP/rQ×aP＝2/1×0．12m/s2＝0．24 m/s2。

（点拨：解决这类问题的关键是把握相同量，找出已知量、待求量跟相同量之间的 关系，即可求解。） 问题争论：①在已知 ap 的状况下，为什么求解 a Q 时应用公式 a＝rω2 而求解 aQ 时，要用公式 a＝v2/r？ ②回忆一下初中电学中学过的导线的阻值消耗的电功率与电流的关系式：P＝I2R 和 P＝U2/R，你能找出电学中的电功率 P 与电流 R 的关系及这里的向心加速度 a 与圆 周半径 r 的关系之间的相同之处吗？ 教师活动 1．出示课堂练习。 2．引导组织教师回顾本节知识。 课堂总结 3． 组织各小组成员在互相合作的基础上， 进行总结。 在互相合作交流的基础上做 4．教师对该堂课的内容进行总结和对学生的小结给 好书面总结。 予肯定跟评判。 听同学总结， 补充修改自己的 5．指出：①掌握如何表示速度的差异量； 书面总结。 学生活动 按照规定完成教学训练。 根据教授提供的信息回顾本 节知识。②匀速圆周运动的加速度的方向是指向圆心的── 向心加速度；③向心加速度的计算式 an==rω2=vω