利用抽屉原理证明素数无穷多

(2)乘法原理：做一件事，完成它需要分成n个步骤，做第一步有m1种不同的方法，做第二步有m2种不同的方法，……，做第n步有mn种不同的方法，那么完成这件事共有n=m1×m2×m3×…×mn种不同的方法． 这里要注意区分两个原理，要做一件事，完成它若是有n类办法，是分类问题，第一类中的方法都是独立的，因此用加法原理。证明方法将地图上的无限种可能情况减少为1,936种状态（稍后减少为1,476种）,这些状态由计算机一个挨一个的进行检查.这一工作由不同的程序和计算机独立的进行了复检.在1996年,neil robertson、daniel sanders、paul seymour和robin thomas使用了一种类似的证明方法,检查了633种特殊的情况.这一新证明也使用了计算机,如果由人工来检查的话是不切实际的.。(a)称为区域d在a点处的映射半径. 黎曼映射定理首先由黎曼(riemann, (g. f. ) b.)于1851年在他的博士论文中给出，他将此问题化为调和函数的狄利克雷问题，并应用狄利克雷原理求解.但魏尔斯特拉斯(weierstrass,k. (t. w.)) 和阿达马(hadamard , j. (-s. ) )指出证明中所用的狄利克雷原理有问题，因而黎曼的证明不能被接受. 随后，便发现了许多方法，找到了狄利克雷问题存在性的证明.如施瓦兹((schwarz,h. a.)的交错法，庞加莱(poincare, (j.-)h.)的扫除法，佩龙(perron , o.)的次调和函数方法，而希尔伯特(hilbert,d.)则完善了黎曼的原论.蒙泰尔(montel , p. a.)应用正规族理论给出定理一个简明的证明.。

第一、素数的公式

公元前300年古希腊的埃拉托斯特尼创造了一种筛法，可以产生任意大的数以内的全部素数： 要得到不大于某个自然数n的所有素数，只要在2—n中将不大于素数的倍数全部划去即可。

上述筛法可以总结为

1，如果n是合数，则它有一个因子d满足1<d≤。

除了1和它自己本身可以整除，不能被其它任何数整除的数是质数，也叫素数。素数就是只能被 1 和自身整除的正整数，1 不是素数，2 是素数。程序分析：判断素数的方法：用一个数分别去除 2 到 sqrt( 这个数 ) ，如果能被整除，则表明此数不是素数，反之是素数。

可以把2的汉字内容等价转换成为英语字母：

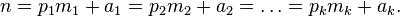.........(1)

其中表示顺序素数2，3，5证明素数有无穷多个，....。≠0。

这样解得的n，若，则n是一个素数。

我们可以把（1）式内容等价转换同余式组表示：

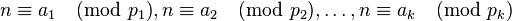..........（2）

由于（2）的模,,...,都是素数，因此两两互素，根据孙子定理(中国剩余定理）知，对于给定的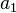,,...,，（2）式在...范围内有唯一解。

范例

例如： k=1时证明素数有无穷多个，，解得n=3，5，7。求得了（3，）区间的全部素数。

第二课时离散型随机变量的方差 求随机变量的方差 [例1]已知随机变量x的分布列为x 0 1 x p p 若ex＝，求dx的值．[思路点拨]解答本题可先根据i＝1求出p的值，然后借助ex＝求出x的取值，最后代入相应的公式求方差．[精解详析]由＋＋p＝1，得p＝.又ex＝0×＋1×＋x＝，x＝2.dx＝2×＋2×＋2×＝.[一点通]求离。 解析答案 (3)求数列{sn}的前n项和. 解由(2)得s1＋s2＋…＋sn 解析答案 应用等比数列前n项和公式时忽视分类讨论致误 易错点 例4等比数列1,2a,4a2,8a3，…的前n项和sn＝.。然而,因大偶数n（不小于6）等于其对应的奇数数列（首为3,尾为n-3）首尾挨次搭配相加的奇数之和.故根据该奇数之和以相关类型质数 质数（1 1）或质数 合数（1 2）（含合数 质数2 1或合数 合数2 2）（注：1 2 或 2 1 同属质数 合数类型）在参与无限次的"类别组合"时,所有可发生的种种有关联系即1 1或1 2完全一致的出现,1 1与1 2的交叉出现（不完全一致的出现）,同2 1或2 2的"完全一致",2 1与2 2的"不完全一致"等情况的排列组合所形成的各有关联系,就可导出的"类别组合"为1 1,1 1与1 2和2 2,1 1与1 2,1 2与2 2,1 1与2 2,1 2等六种方式.因为其中的1 2与2 2,1 2 两种"类别组合"方式不含1 1.所以1 1没有覆盖所有可形成的"类别组合"方式,即其存在是有交替的,至此,若可将1 2与2 2,以及1 2两种方式的存在排除,则1 1得证,反之,则1 1不成立得证.然而事实却是：1 2 与2 2,以及1 2（或至少有一种）是陈氏定理中（任何一个充分大的偶数都可以表示为两个素数的和,或一个素数与两个素数乘积的和）,所揭示的某些规律（如1 2的存在而同时有1 1缺失的情况）存在的基础根据.所以1 2与2 2,以及1 2（或至少有一种）"类别组合"方式是确定的,客观的,也即是不可排除的.所以1 1成立是不可能的.这就彻底论证了布朗筛法不能证"1 1".。

13,43

11,41

17,47

求得了（7，）区间的全部素数。 仿此下去可以一个不漏地求的任何给定数以内的全部素数。由孙子定理知，对于所有可能的值，(1)和(2)式在...范围内，有

（）（）()...（）....（3）个解.

参考文献（清华大学出版社{品数学}）：

二、两个含连续自然数个数相等的区间筛k次被筛数相差不超高k

埃拉特斯特尼筛法是大家熟知的，现在问：两个连续自然数个数相等或者多个自然数相等的区间同时用k个从小到大不同素数筛，被筛掉的数（或者没有被筛掉的数）不同区间会是一样的吗？

将1至...按为一组，划分成...个组（或区间）依次按2,3,5,...顺序筛，筛k次后，任两个含连续自然数个数相等的区间，被筛（或末被筛）数相差不超过k个。

说明：本筛法与埃拉托赛尼筛法不同，埃氏筛先用2筛，然后把2的倍数剔除掉；再用3筛，又把3的倍数剔除掉；再用5筛，.....。本筛法是已经筛过的数不马上剔除掉，而是做上标记，等全部筛完过后再把筛过的数剔除掉。于是，有一些含有几个不同素因子的数就要被筛几遍，例如“6”，就要被“2，”和“3，”各筛一遍。

7．若|a－2|=2－a，则数a在数轴上的对应点在 （a） 表示数2的点的左侧 （b）表示数2的点的右侧……………（ ） （c） 表示数2的点或表示数2的点的左侧 （d）表示数2的点或表示数2的点的左侧 8．计算 的结果是……………………………（ ） （a） （b） （c） （d） 9．下列说法正确的是…………………………………………………………（ ） （a） 有理数就是正有理数和负有理数（b）最小的有理数是0 （c）有理数都可以在数轴上找到表示它的一个点（d）整数不能写成分数形式 10．下列说法中错误的是………………………………………………………（ ） （a） 任何正整数都是由若干个“1”组成 （b） 在自然数集中，总可以进行的运算是加法、减法、乘法 （c） 任意一个自然数m加上正整数n等于m进行n次加1运算 （d）分数 的特征性质是它与数m的乘积正好等于n 二、 填空题：（每题4分，共32分） 11．－0.2的相反数是 ，倒数是 。当原数的绝对值＜1时，n为负整数，n的绝对值等于原数中左起第一个非零数前零的个数（含整数位数上的零）．12．一个数的绝对值是，那么这个数为．【考点】绝对值．【专题】常规题型．【分析】根据绝对值的性质得，|| ，|﹣| ，即可求得绝对值等于的数．【解答】解：因为|| ，|﹣| ，故这个数为．故答案为：．【点评】本题是绝对值性质的逆向运用，此类题要注意答案一般有2个，除非绝对值为0的数才有一个为0．绝对值规律总结：一个正数的绝对值是它本身。二、定理（布金汉定理[泊金汉定理]）1．基本原理：如果一个物理过程涉及到 n个物理量,且n个变量互为函数关系，即:而这些变量中含有m个基本量纲，则这个物理过程可以由n个物理量组成的n-m个无量纲量（相似准则数pi）的函数关系来描述，即:（无量纲项用表示，所以为定理）2．应用步骤（1）找出物理过程有关的物理量 。

现在设某两个区间为A与B，含自然数的个数分别为|A|与|B|，|A|=|B|，下证明p去筛，两区间被筛pm形数（或者未被筛数）个数相差最多不超过1个。由上所述筛法，用顺序素数依次去筛，两区间每次被筛pm形数（或者未被筛数）个数相差最多不超过1个，故筛k次两区间被筛数(或者未被筛数）个数最多不超过k个。

证法1，设|A|=pm+r，则|B|=pm+r，0≤r<p，即区间A和B中均至少含有m个pm形数，又由于r<p，故r个连续自然数中至多有一个pm形数，即被筛pm形数个数相差不超过1个。

证法2，假若不然，筛k次有两个区间A与B，被筛数相差大于K，比如有K+1个，那会出现什么问题呢？我们问第K+1是个什么（见图），例如A与B用2和3去筛，如果出现了相差3个，第一个记为2m形，第二个记为3m形，问第三个（？）是什么形式？（每一个括号表示一个自然数）。

区间A：（+）。。。（+）；------------------------（-）（-）（-）（-）。。。（-）；

区间B：（+）。。。（+）（2m)(3m)(?)；------------------------（-）。。。（-）；

（四）、 试样制备（1）干法制样法：用四分法取代表性试样50 kg，风干碾碎，过50 mm 筛（重型过20 mm或40 mm筛），将筛下土样拌匀，并测定土样的风干含水率，根据土的塑限预估最优含水率，并按gb/t50123-1999标准有关规定制备5个不同含水率的一组试样，相邻两个含水率的差值宜为2%。（2）将试样过2 mm筛，称筛上和筛下的试样质量，当筛下的试样质量小于试样总质量的10%时，不做细筛分析，筛上的试样质量小于试样总质量的10%时，不做粗筛分析（3）将称好试样倒入依次套好的粗筛中，余下的试样倒入依次套好的细筛中，进行筛分。然后将土壤样品于玛瑙研钵中研磨，过20目尼龙筛，混 匀后，取其中部分，再研磨，全部通过100目尼龙筛。

如果第三个（？）是2m或者3m形，显然与除法算式定理矛盾；如果不是2m或者3m形，它就不应该“站在”已经筛过的行列。无论哪一种情况，假设都不能成立。就是说，几个自然数相等的区间，用k个不同的素数去筛，筛完以后，任何两个区间被筛数（或者剩下的数）相差不会超过k个。证毕。

参考内容如下：

第三部分、证明

如果素数只有有限个，最后一个记为，那么（1）式（2）式就就没有小于平方的解。

【1】将1至...按照为一组，划分成...个组（或区间）

[1，]； [，2]； ....； [...—（）+1，...]。

【2】把（1）式（2）式的解数即（3）式（）（）()...（）当做抽屉。

【3】由于假定了（1）式（2）式没有小于的解，第一区间就没有解，因为<，

如果第一区间无解，根据引理：“两个含自然数个数相等的区间筛k次被筛数相差不超k“。其它区间的解数就不会超过k个。

还有.....,个区间，总解数不超过（...）k个。

而：

...) k < （...）k < （）（）()...（）...（4）

【4】 对比（4）式

8 2 8 2 2 8 4 8 点评 分母时, 方程两边同乘各分母的最小公倍数时, 不要漏乘没有分母的 项, 同时把分子 (如果是一个多项式) 作为一个整体加上括号。对应方法：有效数字法(多数乘除取两位，分子不变，分母取前三位有效数字)，错位加减法(精确度高)。3、平均数的增长率：，对应方法：结合分母小于1还是大于1，再根据分子的结果确定选项答案。

647 647 647 646.6 646 646 646 646 646 645.8 645.8 645 645 645 645 644.8 644.6 644 644 644 644 644 644 644 644 644 644 644 644 643 643 643 643 643 643 643 643 643 642.8 642 642 642 642 642 642 641.8 641。石家庄三星冰箱售后服务维修电话：〔1〕400-8359-778〔2〕400-8359-778〔3〕400-8359-778。北京火王燃气灶售后服务电话〔1〕400==8359==315〔2〕400-8359-315。

除了第一项和第二项分母等于分子外，其他都是每一项分子大于分母。

【5】由于抽屉的数量（）（）()...（）是由孙子定理给出的，而装进抽屉的物品（比如乒乓球）.......,) k少于抽屉，至少有一些抽屉是空的，这样就违反了孙子定理，与孙子定理矛盾，必然是错误的。所以，原先假设最后一个素数是，显然是错误的，素数无穷多个。

证毕。