微分中值定理81768.ppt

分析：把要求零点的函数，变成两个基本初等函数，根据所给的a，b的值，可以判断两个函数的交点的所在的位置，同所给的区间进行比较，得到n的值．解答：解：设函数y=logax，m=﹣x+b根据2＜a＜3＜b＜4，对于函数y=logax 在x=2时，一定得到一个值小于1，在同一坐标系中划出两个函数的图象，判断两个函数的图形的交点在（2，3）之间，∴函数f（x）的零点x0∈（n，n+1）时微分中值定理，n=2微分中值定理，故答案为：2点评：本题考查函数零点的判定定理，是一个基本初等函数的图象的应用，这种问题一般应用数形结合思想来解决．三、解答题（共6小题，满分74分）17．（2011。11应用radians函数将角度转换为弧度18312应用sin函数计算给定角度的正弦值18413应用sinh函数计算某数字的双曲正弦值18514应用tan函数计算给定角度的正切值18515应用tanh函数计算某一数字的双曲正切1864综合实战：计算员工加班费187第7章信息函数1881信息函数概述1882is类函数1891应用isblank函数判断单元格是否为空白1902应用iserr或iserr。cosh函数计算数字的反双曲余弦值1753应用asin函数计算数字的反正弦值1764应用asinh函数计算数字的反双曲正弦值1775应用atan函数计算数字的反正切值1786应用atanh函数计算数字的反双曲正切值1797应用atan2函数计算x及y坐标值的反正切值1808应用cos函数计算角度的余弦值1819应用cosh函数计算数字的双曲余弦值18110应用degrees函数将弧度转换为度182。

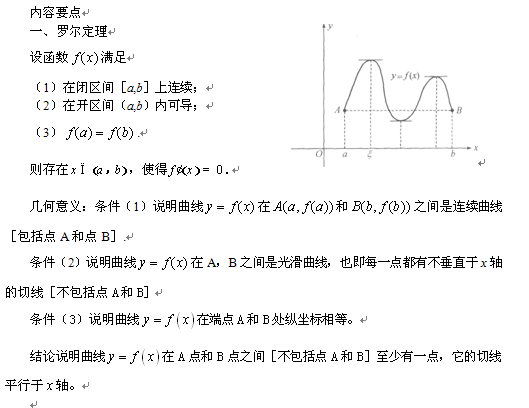
若 M = m , 则 因此 在( a , b ) 内至少存在一点 不妨设 则至少存在一点 使 注意: 1) 定理条件条件不全具备, 结论不一定 成立。 则由费马引理得 例如, 使 本定理可推广为 在 ( a , b ) 内可导, 且 在( a , b ) 内至少存在一点 证明提示: 设 证 F(x) 在 [a , b] 上满足罗尔定理 。 有且仅有一个小于1 的 正实根 。 证: 1) 存在性 。 则 在 [0 , 1 ] 连续 , 且 由零点定理知存在 使 即方程有小于 1 的正根 2) 唯一性 。 假设另有 为端点的区间满足罗尔定理条件 , 至少存在一点 但 矛盾, 故假设不真! 设 在 内可导, 且 证明至少存在一点 使 上连续, 在 证: 问题转化为证 设辅助函数 显然 在 [ 0 , 1 ] 上满足罗尔定理条件, 故至 使 即有 少存在一点 满足下述等式 证明方程 在 ( 0 , 1) 内至少有一 个实根 。 证: 令 则可设 且 由罗尔定理知存在一点 使 即 (1) 在区间 [ a , b ] 上连续 满足: (2) 在区间 ( a , b ) 内可导 至少存在一点 使 思路: 利用逆向思维找出一个满足罗尔定理条件的函数 作辅助函数 显然 , 在[a, b] 上连续, 在(a, b)内可导, 且 证: 问题转化为证 由罗尔定理知至少存在一点 即定理结论成立 。

拉氏 证毕 A B C 推论: 若函数 在区间 I 上满足 则 在 I 上必为常数。 证: 在 I 上任取两点 格朗日中值公式 , 得 由的任意性知, 在 I 上为常数 。 令 则 若函数 在区间(a , b)内每一点 x 处都有 则 和 最多相差一个常数, 即 (其中C为常数)。 设 证明对任意 有 证： 不妨设 证: 设 由推论可知 (常数) 令 x = 0 , 得 又 故所证等式在定义域上成立。 自证: 经验: 欲证 时 只需证在 I 上 证: 设 中值定理条件, 即 因为 故 因此应有 在 内可导, 且 证明 在 内有界。 证: 取点 再取异于 的点 对 为端点的区间上用拉氏中值定理, 得 (定数) 可见对任意 即得所证 。 分析: 及 (1) 在闭区间 [ a , b ] 上连续 (2) 在开区间 ( a , b ) 内可导 (3)在开区间 ( a , b ) 内 至少存在一点 使 满足 : 问题转化为证 柯西 构造辅助函数 且 使 即 由罗尔定理知, 至少存在一点 思考: 柯西定理的下述证法对吗 ? 两个 ? 不 一定相同 错! 上面两式相比即得结论。

注意: 弦的斜率 切线斜率 A B C 至少存在一点 使 证: 问题转化为证 设 则 在 [0, 1] 上满足柯西中值 定理条件, 因此在 ( 0 , 1 ) 内至少存在一点 ? , 使 即 证明 使 证: 法1 用柯西中值定理 。 则 f (x) , F(x) 在 [ 1 , e ] 上满足柯西中值定理条件, 令 因此 即 分析: 使 法2 令 则 f (x) 在 [ 1 , e ] 上满足罗尔中值定理条件, 使 因此存在 1。 微分中值定理的条件、结论及关系 罗尔定理 拉格朗日中值定理 柯西中值定理 2。 微分中值定理的应用 (1) 证明恒等式 (2) 证明不等式 (3) 证明有关中值问题的结论 关键: 利用逆向思维 设辅助函数 费马引理 1。 填空题 1) 函数 在区间 [1, 2] 上满足拉格朗日定理 条件, 则中值 2) 设 有 个根 , 它们分别在区间 上。 方程 且在 内可导, 证明至少存 在一点 使 提示: 由结论可知, 只需证 即 验证 在 上满足罗尔定理条件。 设 可导, 试证在其两个零点间一定有 的零点。 提示: 设 欲证: 使 只要证 亦即 作辅助函数 验证 在 上满足 罗尔定理条件。

即 当 时 问是否可由此得出 不能 ! 因为 是依赖于 x 的一个特殊的函数。 因此由上式得 表示 x 从右侧以任意方式趋于 0 。 应用拉格朗日中值定理得 上对函数 P1347, 8 , 10 , 12 , 14 , *15 提示: 题*15。 题14。 考虑 第二节 费马 法国数学家, 他是一位律师, 数学 只是他的业余爱好。 他兴趣广泛, 博 览群书并善于思考, 在数学上有许多 重大贡献。 他特别爱好数论, 他提出 的费马大定理: 历经358年, 直到1993年才由美国普林斯顿大学的安德 鲁。怀尔斯教授经过十年的潜心研究才得到解决 。 引理是后人从他研究解决最值的方法中提炼出来的。 法国数学家。 他在方程论, 解析函数论, 及数论方面都作出了重要的贡献, 近百 余年来, 数学中的许多成就都可直接或 间接地追溯到他的工作, 他是对分析数学 产生全面影响的数学家之一。 法国数学家, 他对数学的贡献主要集中 在微积分学, 《柯 西全集》共有 27 卷。 其中最重要的是为巴黎综合学校 编写的《分析教程》, 《无穷小分析概论》, 《微积分 在几何上的应用》 等, 有思想有创建, 广泛而深远 。 对数学的影响 他是经典分析的奠基人之一, 他为微积 分所奠定的基础推动了分析数学的发展。 复变函数和微分方程方面 。 一生发表论文800余篇, 著书 7 本 , * 目录 上页 下页 返回 结束 * * * *