：对数函数的运算、性质以及幂函数图像性质(图)

----. 可修改。对数函数的运算和性质和幂函数的图像性质 一、 对数函数的运算1、 对数的定义：如果 ax=N(a>0, a≠1） 那么数 x称为以a为底数N的对数。表示为：x=logaN，其中ia为对数的底数，N为真数，x=logaN为对数。常用对数：Log10N=lgN 自然对数: logeN=lnN2、 指数与对数表达式的联系： 指数对数3、 对数运算性质 若a>0, a1, M>0, N>0 有:;语言表,党员人数考核表和毫米对照表、教师职称等级表、员工考核得分表、普通年金现值系数表达式：两个正数的乘积的对数等于两个正数的对数与两个正数的商的对数等于这两个正数的对数差。一个正数的 n 次方的对数等于这个正数的 n 倍的对数。给出四个等式：4、对数转换公式(a>0,a1,m>0,m1,N>0)两个推论：设a,b>0且都不是1、那么；二、对数函数图像和属性三、幂函数图像和属性1.定义幂函数的形式为y=xa的函数称为幂函数，其中a是一个常数，a∈R2.幂函数的定义域：是一组实数使 xa 有意义。它不随

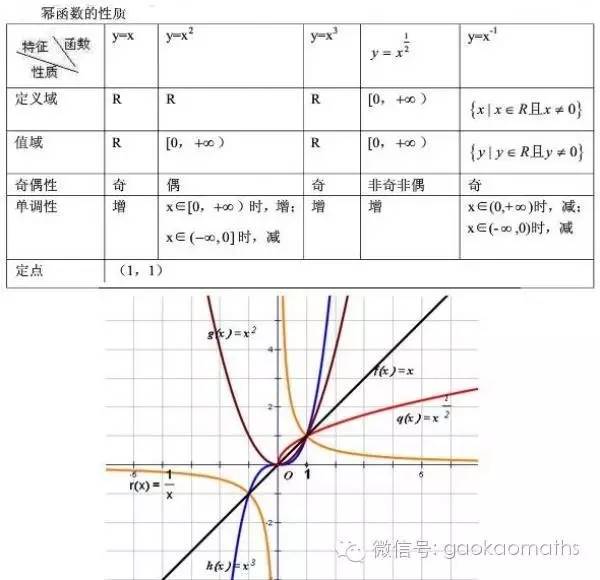
相同幂函数和指数函数的比较。命名a（常数）X（自变量）Y（函数值）指数函数：y=ax基指数幂值幂函数：y=xa指数基幂值判断一个函数是幂函数还是指数函数入口点看未知数 x 是指数或基幂函数 y=x, y=x2, y=x3, y=x1/2, y=x-1 图片：函数属性 y=xy=x2y =x3y=x-1 定义范围RRR[0,+∞){x|x≠0} 取值范围 R[0,+∞)R[0,+∞){y|y≠0} Parity, Odd, Odd Odd 非偶奇单调递增[ 0, +∞)增加增加增加(0,+∞)减少(-∞,0]减少(-∞,0)减少公共点(1,1)测试点) 1 对数函数计算实例，乘法，口算，100题，七年级有理数混合计算，

. 例如问题2，我们知道lg2=a，lg7=b，那么log898=________。变体训练2知道a=log32，用a来表示log38-2log36就是例子问题3，设3x=4y=36，求eq\f(2, x)+eq\f(1,y)的值。Variant training 3 如果lg2=a,lg3=b，那么eq\f(lg15,lg12)等于扩展训练1。已知lna+lnb=2ln(a-2b)，求log2eq\f(a ,b) Variant training 4 的值被设置，那么 和 之间的关系是 ABCD 和 之间的关系是不确定的 测试点 2 对数函数的性质 对数函数的概念、形象和性质，设计对数的域、范围、类型函数的单调性等问题。4、已知函数的例子，（1）求函数的定义域；（2）判断奇偶性对数函数教案下载，并说明原因；​​（1）3） 探索其领域的单调性。例 5. 求下列函数的定义域、范围和单调区间： ⑴; ⑵（和）。例6 如果区间是递增函数，则X的值是变异训练的已知函数5、，（1）求域；（2）求单

调谐间隔；（3）求最大值，求最大值时求x的值。Variant training 6 已知对数函数教案下载，求m的值 x 周长variant training 7 求函数值的最大值和最小值。例8 已知函数满足条件（1）求出的表达式；（2）求函数的域；（3）判断的奇偶性与实数的关系例9 已知函数为（ ) A. 是奇函数 也是偶函数 B. 偶函数 C. 奇函数 D. 既不是奇函数也不是偶函数 测试点 3 树组合示例 10. 知道它是方程的根，是方程的根，则+=. 测试点4 幂函数例11.的图像和性质 图中曲线是幂函数y=xn在第一象限的图像。已知n取±2和±eq\f(1,2)四个值，那么曲线C1,C2,C3,C4对应的n为()A.-2,-eq\f (1,2),eq\f(1,2), 2B.2, eq\f(1,2), -eq\f(1,2), -2C. -eq\f(1,2), -2,2,eq\ f(1,2)D．2,eq\f(1,2), -2 , -eq\f(1,2)

例12.令α∈{－2,－1,－eq\f(1,2),eq\f(1,2),1,2,3},已经知道幂函数f(x)=xα是偶函数，在区间(0,+∞)内是递减函数，满足条件的α值个数为()A.1B。 2C.3D.4 例1 3.已知函数f(x)=(a－1)·xa2＋a－1.当a=______时，f(x)为比例函数；当a=______时，F(x)为反比函数；当a=______时，f(x)为二次函数；当a=______时，f(x)为幂函数。如果点(eq\r (2), 2) 在幂函数 f(x) 的图像上，点 (-2, -eq\f(1,2)) 在幂函数 g 的图像上(x), 问x的值是多少, (1)f(x)>g(x); (2)f(x)=g(x); (3) f(x)

(2)确定f(x)的奇偶性和单调性；(3) 对于f(x)，当x∈(- 1. 当1)时，有f(1－m)+f(1－m2)