高一数学上册第三单元知识点：对数与对数函数，希望能帮助大家学习

一般将函数y=logax(a>0, and a≠1)称为对数函数，即以幂(真数)为自变量，以指数为因变量的函数变量，一个常数的底叫做对数函数，以下是一年级数学第三单元的知识点：对数和对数函数，希望对大家学习有帮助！

一般而言，若a(a大于0，且a不等于1)的b次方等于N，则b称为以a为底的N的对数，记为log( a)(N)=b ，其中a称为对数的底数，N称为真数。

基数必须大于 0 而不是 1

对数运算的性质

当a>0且a≠1时，M>0，N>0，则：

(1)log(a)(MN)=log(a)(M)+log(a)(N);

(2)log(a)(M/N)=log(a)(M)-log(a)(N);

(3)log(a)(M^n)=nlog(a)(M) (n∈R)

(4) 基础交换公式：log(A)M=log(b)M/log(b)A (b>0 and b≠1)

对数与指数的关系

当a>0且a≠1时，a^x=N x=㏒(a)N

常用缩写词

(1)常用对数：lg(b)=log(10)(b)

(2)自然对数：ln(b)=log(e)(b)

(3) log(a)+(b)=log(a)(b)

e=2.718281828... 通常只有 e=2.71828

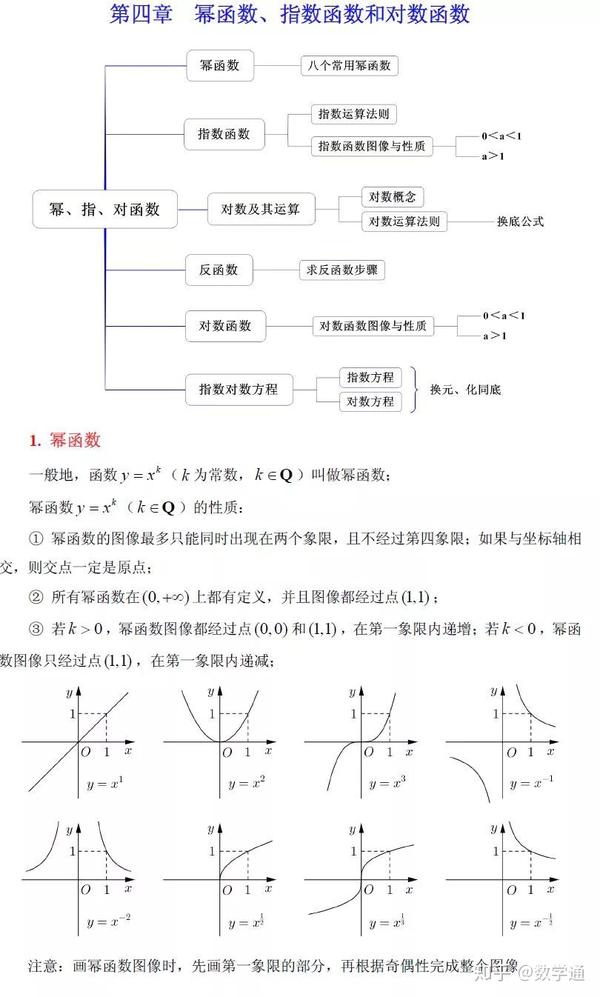
对数函数的定义

对数函数的一般形式是y=㏒(a)x，实际上是指数函数的反函数（图像关于直线y=x的两个对称函数互为反函数），即可以表示为 x=a^y 。因此，指数函数中a的规定（a>0和a≠1)）也适用于对数函数。

右图为不同尺寸a的函数图：

可以看出，对数函数的图形只是指数函数的图形和关于直线y=x的对称图形，因为它们互为反函数。

定义范围：(0, +∞) 取值范围：实数集R

不动点：函数图像总是通过不动点(1, 0).

单调性：当a>1时，是定义域和凸域中的单调递增函数；

Parity：非奇非偶函数

周期性：不是周期函数

零点：x=1

知识拓展：

16世纪末至17世纪初，自然科学（尤其是天文学）的发展经常遇到大量精确而庞大的数值计算，因此数学家为了寻找简化的计算方法而发明了对数。.

在德国史提非（1487-1567) 1544年）所著的《整数的算术》中，他写了两个数列，左边是等比级数（称为原数），右边是算术级数系列。（称为原数的代表，或指数，德语为Exponent，意为代表）。

求左边任意两个数的乘积（商）对数函数教案下载，只要先求其代表（指数）的和（差），然后把这个和（差）与左边的一个原数对立，再把这个原数就是你想要的乘积（商），遗憾的是，史提非没有做进一步的探索，也没有引入对数的概念。

纳皮尔在数值计算方面有很多研究。他制作的“纳皮尔计算器”简化了乘法和除法运算。其原理是用加法和减法代替乘法和除法。他发明对数的动机是为球面三角找到一种方便的方法。他基于与粒子运动相关的一个非常独特的想法构建了所谓的对数方法。其核心思想表现为等差数列与几何数列的关系。连接。他在《奇妙对数表的描述》中阐明了对数原理，后人称为纳皮尔对数，记为Nap.㏒x，它与自然对数的关系为Nap.㏒x=107㏑(107/x) )

可见，纳皮尔的对数既不是自然对数，也不是常用的对数，与当前的对数有一定的距离。

瑞士表旗（1552-1632)也独立发现了对数，可能比纳皮尔更早，但发表较晚（1620).

英国的布里格斯于 1624 年创造了常用对数。

1619 年，Peter London 的“新对数”使对数更接近自然对数（基于 e=2.71828...）。

对数的发明对当时社会的发展产生了重要影响。正如科学家伽利略（1564-1642)）所说：“给我时间、空间和对数，我可以创造一个宇宙。”又如十位八世纪数学家拉普拉斯（1749-1827)还提到：“对数缩短了计算时间，使天文学家的寿命增加了一倍。”

最早引入我国的对数著作是《比例与对数》对数函数教案下载，由波兰的穆尼斯（1611-1656)）和我国的薛丰佐于17世纪中叶编撰。当时在lg2=0.3010中，2被称为“真数”，0.3010被称为“假数”。真数和假数列在一张表中，故称为对数表。后来，使用了“假数”。它是“对数的”。

我国清代数学家戴旭（1805-1860)）开发了多种求对数的捷径，着有《简化对数》（1845)，《续对数简化》） ” The Law (1846), etc.) 1854年，英国数学家约瑟夫·艾（1825-1905)）看到这些作品，印象深刻。

现在的中学数学课本先讲“指数”，然后以反函数的形式介绍“对数”的概念。但在历史上，恰恰相反，对数的概念并不是来自指数，因为当时有一个明确的未经证实的指数和无理指数的概念。Briggs 曾向 Napier 提议用幂指数表示对数。1742年，J.威廉（1675-1749)）在G.威廉的“对数表”的前言中做了指数可定义的对数。 @> 明确说明对数函数是指数函数的反函数，这与现在的教科书表述是一致的。

【一年级数学第一卷对数和对数函数的知识点】相关文章：

1.高中数学知识点：对数函数

2.高考必考数学：对数和对数函数

3.“对数函数”的高一必修知识点

4.高中数学对数函数公式排列

5.对数函数数学教学计划

6.中考数学知识点：对数函数和幂函数

7. 《对数函数的应用》数学教学计划

8.高中二年级数学对数函数图像及性质