对数函数教案下载(高中数学：对数函数的性质(1)(图))

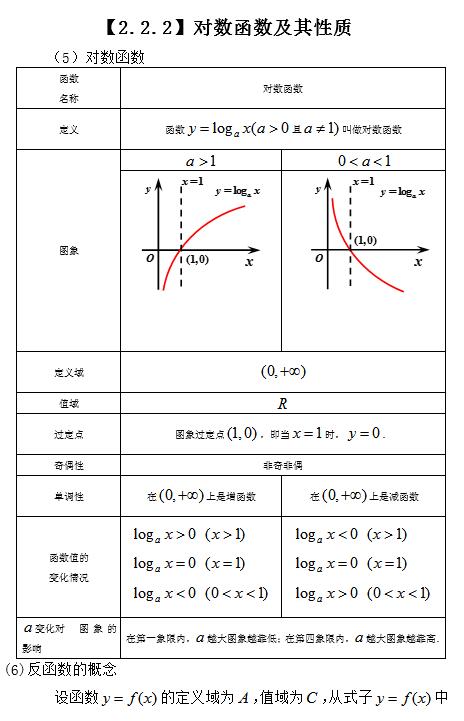
欢迎。指导教学目标：1.会画对数函数的图形并解决相应的问题。 2. 掌握对数函数的性质，能够解决与域、范围、单调性、奇偶性等相关的综合问题。 1.Logarithm 性质和运算规则（1)Logarithm 运算规则如果a>0且a≠1，M>0，N>0，则①loga(MN)=logaM＋loga；N②logaMN=logaM－loga；N③logaMn=nlogaM（ n∈R);④logam Mn= (2)对数性质n mlogaM .①aloga N=N;②logaaN=N (a>0 and a≠1)．(3)罗数的) 重要公式 ①变基公式：logbN=logaN logab(a,b均大于零且不等于1)；②logab=log1ba，概括logab·logbc·logcd=logad。2.对数函数a>当101时的形象和性质, y>0 当(5)当x>1, y0(6)是(0, +∞)上的增函数) (7)是(0, +∞)上的减函数3.Inverse函数指数函数 y=ax 和对数函数 y=logax 互为反函数，它们的图像关于直线 y=x 对称，域为 (0, +∞)对数函数教案下载，值域为 R，在不动点(1 ,0)。当a>1时，y=logax是(0,+∞)上的递增函数。当00时，a≠1)如图，关系a， b满足是(A)A.01；和 -1f(a+1)Cf(b-2)1, 所以 f(b-2)=f(2), 同样 a>1, ∴a+1>2 , 从 f(x) 单调在 (0, +∞) 上递增，我们知道 f(a+1)>f(2)，即 f(a+1)>f(b-2))，答案是 C。题型二对数函数例2 对于函数fx log 1 (x 2 2 ax 3)，回答下列问题： 2(1)如果f(x)的定义域为R，求取值范围实数 a ；（2)如果 f(x) 的取值范围为 R，求实数 a 的取值范围；（3)如果函数 f(x) 在 (-1, +∞)，求实数a的值；(４)如果函数f(x)的定义域是(-∞,1)∪(3,＋∞))，求实数a；(５)若函数f(x)为(-∞,-1)，求实数a的值；(6)如果函数f(x)是(- ∞,1)对数函数教案下载，求实数a的取值范围。(4)由问题暗示x2-2ax+3>0的解集为(-∞,1)∪(3,+∞) ，即x2-2ax+3=0有两个根1、3，问题蕴涵es 1+ 3=2a, a=2 ∴当a=2时，函数f(x)的定义域为(-∞,1)∪(3,+∞) .5 由题意(x 2 2 ax 3 )m in 1 2 4 4 a 2 2, a 1 ，则a的取值范围为1,2。点评：研究y=logaf(x)形式的函数的单调性时，必须保证函数的定义域，必须注意复合函数的单调性。总结一：对数函数图的知识总结。找到函数的定义域和自变量 x。解决不等式（方程）。单调区间问题。判断平价，优先领域（领域是函数的生命。如果失去函数的生命，你就会失去它。我的生命） 总结二：数学思想和方法，将思想与图形和形状相结合，转化为想法，改变元素，类比课业1.为了得到y lg x 3 10的图像，只需要函数y=lgx Point()在图像A上向左平移3个单位长度，然后1个单位B. 向右平移 3 个单位长度，然后向上平移 1 个单位长度 C. 向左平移 3 个单位长度，向下移动 1 个单位长度 D. 向右移动 3 个单位长度，然后向下移动 1 个单位长度 2.函数 y log 1 (2 x 2 3 x 1) 的递减区间为 ________23. 给定函数 f(x)=lg(ax2+2ax+1) 的定义域为 R，实数 a∈ ________.4.known function fxx+log21 1 xx, then f20110+f20109+f20108f20108f20109f20110________2 5.设置f(x)=lg(1 x +a) 是奇函数，那么f(x)

教案网123