【每日一题】由莲山课件提供资源全部免费

由莲山课件提供 资源全部免费第18课时一次函数（1）八（上）第五章5。1～5。3［课标要求］1、了解常量、变量的涵义，函数的概念跟三种表示方式。2、结合图象对简单实际问题的变量关系进行预测。3、确定简单函数式中和简单实际问题中的方程的自变量的取值范围，并求出函数值。4、用适度的变量表示法塑造这种实际问题中变量之间的关系，分析函数关系、预测变量的差异规律。5、结合具体语境体会一次函数和正比例函数意义，根据已知条件确认一次函数关系式6、会画一次函数的图象，能根据一次函数的图象或关系式y＝kx＋b（k≠0）探索并理解其性质（k＞0或k0时，图像的变化情况）［基础训练］1、下列方程中，自变量x的取值范围为x＜1的是（）A、B、 C、D、2、如果正比例函数的图像经过点（1，－2），那么k 的值等于＿＿＿＿＿＿．3、已知一次函数y＝－3x＋2，它的图像不经过第＿＿＿＿＿＿象限。4、若一次函数的函数值随的减少而增加一次函数教案格式，且图像与轴的负半轴相交，那么对跟的符号判断正确的是（）A、B、C、D、5、两直线的交点坐标为（）A、（—2，3）B、（2，—3）C、（—2，—3）、（2，3）6、下列曲线中，表示不是的函数是 （ ）AxyOBxyOCxyODxyO由莲山课件提供 资源全部免费由莲山课件提供 资源全部免费［要点梳理］1、函数的定义：＿＿＿＿＿＿＿＿＿＿2、确定自变量的取值范围：一般需从两个方面考量①自变量的取值需要让其所在代数式有含义；②使实际问题有含义3、函数的三种表示方式：（1）＿＿＿＿＿＿；（2）＿＿＿＿＿＿；（3）＿＿＿＿＿＿4、一次函数的定义：＿＿＿＿＿＿＿＿＿＿那么y叫做x的一次函数，当＿＿＿＿时，一次函数y＝kx＋b就作为y＝kx（k是系数，k≠0）这时y叫做x的正比例函数（或者说y与x成正比例）5、一次函数的图像是＿＿＿＿＿，其性质是：（1）k＞0，b＞0时，图象过第＿＿＿＿＿＿象限；（2）k＞0，b＜0时，图象过第＿＿＿＿＿＿象限；（3）k＜0，b＞0时，图象过第＿＿＿＿＿＿象限；（4）k＜0，b＜0时，图象过第＿＿＿＿＿＿象限；6、画正比例函数的图像，一般取＿＿＿＿＿两点，画一次方程的图像，一般取直线与坐标轴的两交点。

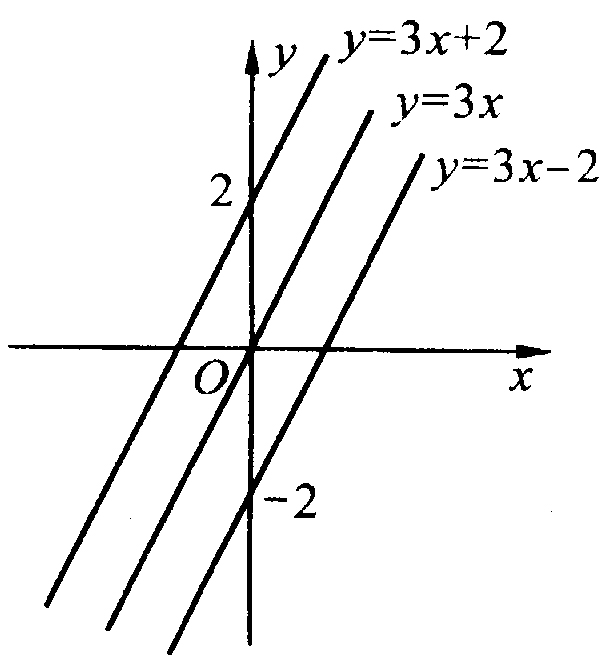
7、求函数解析式的通常办法是待定系数法。［问题研讨］例1、如图，A、B、C、D为圆O的四等分点，动点P从圆心O出发，沿的路线作匀速运动．设运动时间为t秒，∠APB的度数为y度，则以下图像中表示y（度）与t（秒）之间的函数关系更正确的是（）（2）已知梯形ABCD的四个顶点的坐标分别为A（－1，0），B（5，0），C（2，2）一次函数教案格式，D（0，2），直线y=kx+2将矩形分成体积相同的两部份，则k的值为（）由莲山课件提供 资源全部免费由莲山课件提供 资源全部免费A、 －B、 －yxAOB第2题图C、 －D、 －2、如图，点A的坐标为（－1，0），点B在直线y＝2x－4上运动，当直线AB最短时，点B的坐标是___________。［规律总结］1、在用解析式表示方程时，要考量自变量的取值范围，必须让解析式有含义，一般地，当解析式是方程时，自变量的取值范围是一切实数；解析式是等式时，自变量的取值范围是乘数不为0的一切实数，解析式含有二次根式时，自变量的取值范围是被开方数≥0；2、通过待定系数法的复习，了解代数思想在解题中的应用；3、本单元的主要考点为：①正比例函数和一次方程的概念；②实际问题中方程自变量的取值范围；③函数的增减性，图像位置与k、b的关系；④图像与坐标轴（或有关直线）围成的图形面积；⑤待定系数法和方程思想。

［强化训练］1、函数y＝，自变量x的取值范围是（）A、x≥0B、x＞0且x≠1C、x＞0D、x≥0且x≠12、将直线 y = 2 x ─ 4 向上平移5个单位后，所得直线的表达式是____ __。3、已知一次函数与的图像交于点，则点的坐标为．4、一次函数y=kx+b中，k0,b0。那么它的图像不经过（）A、第一象限 B、第二象限C、第三象限D、第四象限由莲山课件提供 资源全部免费由莲山课件提供 资源全部免费5、如图，直线y=kx+b经过A（3,1）和B（6,0）两点，则不等式0＜kx+b＜的解集为________。6、小丁每天从报社以每份0。5元买进报纸200份，然后以每份元卖给读者，卖不完，当天能退回，但只按0。2退给，如果平均卖出x，纯收入为y。（1）求y与x之间的方程关系式（要求写出自变量x的取值范围）；（2）如果每年30天计算，至少要买多少能够确保每年开支不超过2000元？由莲山课件提供 资源全部免费