【知识梳理】等腰三角形的定义及性质形性质

一知识梳理：

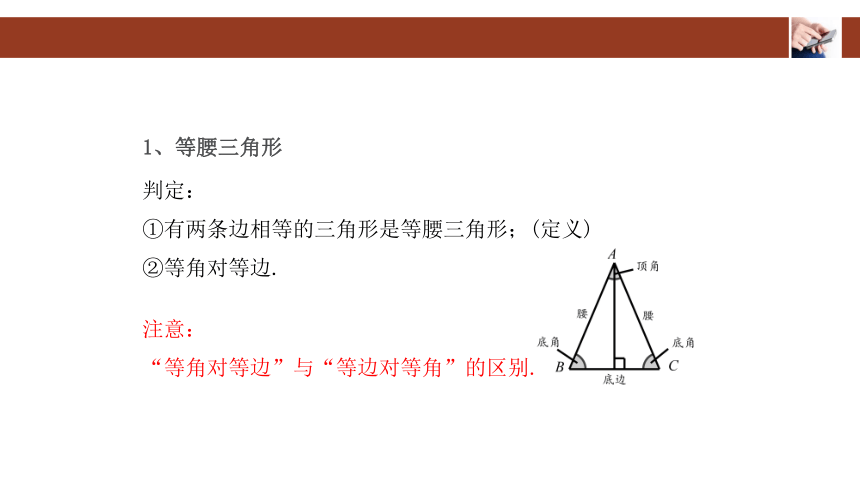
等腰三角形的定义

1、等腰三角形

两条边相等的三角形叫等腰三角形，两条相等的边叫腰，另一边叫底，两腰的夹角叫顶角，底与腰的夹角称为底角。

如图所示，在△ABC中，AB=AC，△ABC是等腰三角形等腰三角形知识点及典型习题教案模板3，其中AB和AC是边，BC是底，∠A是顶角，∠B和∠C是基角。

2、等腰三角形的练习

已知线段a、b（如图）。用尺子和圆规做一个等腰三角形ABC等腰三角形知识点及典型习题教案模板3，使AB=AC=b，BC=a。

练习：1.使线段BC=a；

2. 以b和c为圆心，b为半径画一条圆弧，两条圆弧

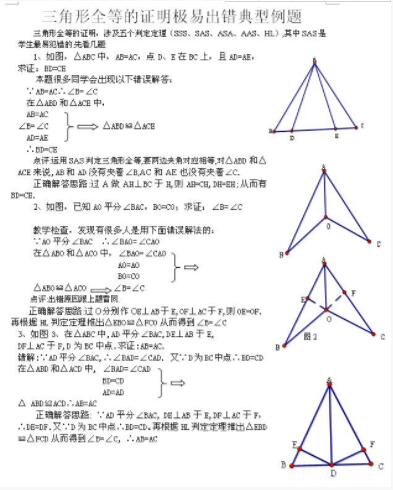
相交于 A 点；

3.连接 AB、AC。

△ABC是想要的等腰三角形

3、等腰三角形的对称性

(1)等腰三角形是轴对称图形；

(2)∠B=∠C;

(3)BD=CD, AD 是底边的中心线。

(4)∠ADB=∠ADC=90°，AD是底边的高线。

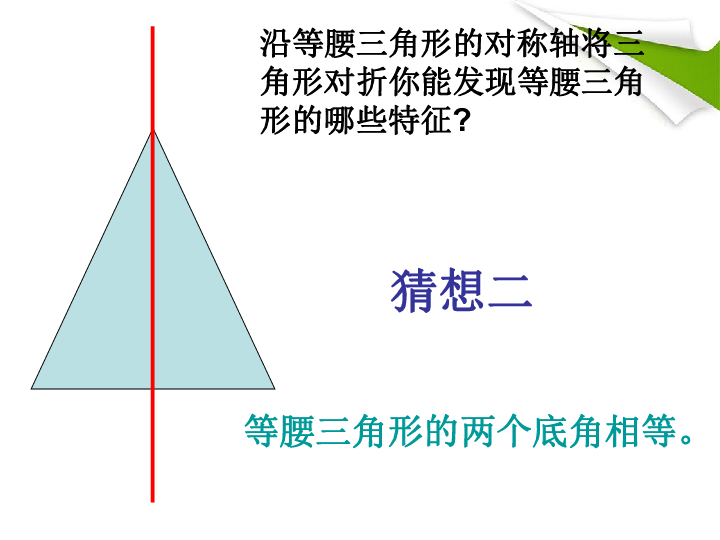
结论：等腰三角形是一个轴对称图形，顶角平分线（底边的高线或中线）所在的直线就是它的对称轴。

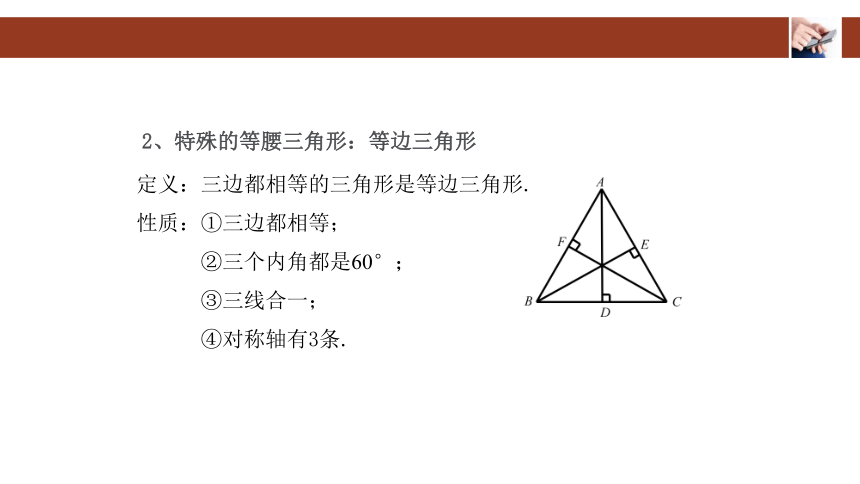
4、等边三角形

三边相等的三角形称为等边三角形。也称为等边三角形。等边三角形是一类特殊的等腰三角形，它具有三个对称轴，每个角的平分线（底边的高线或中线）它所在的线就是它的对称轴。

关键点：

(1）等腰三角形的底角只能是锐角，不能是钝角（或直角），但顶角可以是钝角（或直角）。∠A＝ 180°－2∠B，∠B＝∠C=

.

(2）等边三角形和等腰三角形的关系：等边三角形是特殊的等腰三角形，等腰三角形不一定是等边三角形。

等腰三角形的性质

1.等腰三角形的性质

性质1：等腰三角形的两个底角相等；

推论：等边三角形的三个内角都相等，每个内角都等于60°。

性质2：等腰三角形顶角的平分线、上中线和底高线重合。

2.等腰三角形中重要线段的性质

等腰三角形的两个底角的平分线（两边高，两边中线）相等。

要点：这个性质还可以推广到以下结论：

（1）等腰三角形底边上任意一点到两腰的距离相等。

(2）等腰三角形两个底边的中点到两条边的距离相等。

(3）等腰三角形的两个底角的平分线，两腰的中线，两腰的高与两腰的交点等距，两端的距离基数相同。

(4）等腰三角形的顶点到两边的高、中线、角平分线的距离相等。

等腰三角形判断定理

1、等腰三角形判断定理

如果两个角相等，则三角形是等腰三角形。可以简单地说：在三角形中，相等的角等于相等的边。

要点：(1)澄清判断定理的条件和结论，不要与性质定理混淆。从判断定理得到的结论是等腰三角形，性质定理是已知的三角形是等腰三角形，得到边与角的关系。

（2） 不能说“两个底角相等的三角形，那么两条边相等”，因为它还没有被确定为等腰三角形。

2、确定等边三角形的定理

三个等角的三角形是等边三角形。

一个角为60°的等腰三角形是等边三角形。