2011版中小学数学新课标标准(2011年版)附录2内容标准及实施建议

教育部公布了《义务教育数学课程标准（2011年版）》，以下是2011年版中小学数学新课程标准。

2011版中小学数学新课标：附录2（数与代数）

《义务教育数学课程标准（2011年版）》附录2内容标准及实施建议示例

第一阶段（1-3 年级）数字和代数

例 1 用算盘上的珠子表示三个数字。

【解说】算盘是我国的一项重大发明，体现了十进制的计数。算盘最大的特点是：下珠表示1，上珠表示5。使用算盘时要注意以下两点：

(1）先确定个位，先任意选择一个文件作为个位，再左移到十、百、千等。

（2）用珠子来表示数字。一个位上的几个表示几个，十位上的几个表示十位……如果一个数字为0，则表示为没有珠子的空格。

比如513，在算盘上是

更大的数字可以用相同的方式表示。

例2 对数字50、98、38、10、51进行排序小学数学数与代数教案模板，用“>”或“<”表示。进一步用大得多、大得多、小得多、小得多等来描述它们之间的关系。

[说明] 符号“>”或“<”表示量之间的关系。希望学生能理解符号的含义并合理使用。这个过程可以帮助学生建立数感。

要求学生对这些数字进行排序，学生可能有不同的排序方法。比如先找到最小的（最大），然后在剩下的数字中找到最小的（最大），然后将五个数字按照从小（大）到大（小）的顺序排列；或者先固定一个数（比如50），取第二个数（98）与它比较，再取第三个数与前两个数比较，确定根据它们之间的大小关系定位，以此类推，最后对五个数字进行排序。不管学生的出发点是什么，只要思路清晰，排序正确。

当用语言来描述几个数之间的大小关系时，结论是相对的。比如可以说51比50大，98比10大很多；而 50 比 38 大还是比 38 大得多，可能有不同的看法，但应该没有逻辑上的混淆，例如“50 比 10 大，50 比 38 大得多”。

示例 3 1200 张纸有多厚？您的 1 200 步大约需要多长时间？1200名学生站队进行广播练习需要多少空间？

【解说】通过理解1 200在不同情境下的意义，感受数量与生活现实的关系。以上三个问题类似，学生可以从一个案例中学习推论。

对于“1 200张纸有多厚”这个问题，在教学中可以做如下设计：

（1）一本数学课本大约有50张纸装订。可以让学生先观察自己的课本，感受一本书的厚度。

（2）将10本教材叠放在一起，让学生感受每增加一本的论文数量，感受从小数增加到大数出现的过程。

（3）想想1200张纸有多厚？（如果10本书是500张纸，学生可以想象20本书是1000张纸，1200张纸是20多本书) 厚）让学生描述“这 1200 张纸叠在一起有多高”，并鼓励学生从不同角度描述。

例 4 说出与日常生活密切相关的数字及其表达的事物。

【解说】对于小学生来说，日常生活中使用数字的例子很多，比如学号、班级规模、身高、价格、体重、距离等。其他，从而实现数字的意义和功能。

例 5 教室有 6 排座位，每排有 7 个座位。教室里有几个座位？

【说明】这个例子可以引导学生理解，一个教室的座位数是6个7之和，可以写成：6×7或7×6。

例6 学校组织987名学生到公园玩耍。如果公园门票8元一张，带8000元够吗？

【说明】这个例子的目的是希望学生理解在什么情况下需要进行估计。能够根据具体情况选择合适的单元是第一学期预估的核心。例如，本例中合适的方法是将 987 人视为 1000 人，因此合适的单位为“1000 人”。

一般来说，估算教室的长度时，通常以“米”为单位；在估算一本书的长度时小学数学数与代数教案模板，通常以“厘米”为单位。也可以以周围熟悉物体的长度为单位，如步长、臂长等。

例 7 每条船限 4 人，18 人最少需要租几条船？您认为正确的分配方式是什么？

示例 8 估计每分钟的节拍次数、阅读的单词数、跳绳的数量以及所走的步数。

【解说】这个例子不仅可以帮助学生体验1个点的长度，而且是一个估计问题，需要实际测量，根据测量进行简单计算。

实际测量可采用三种方法：测量半分钟，然后将测量数据乘以 2；测量 1 分；测量2个点，然后将测量的数据除以2。对于能学到更多知识的同学，可以引导他们意识到第一种方法比较麻烦，但可能不够准确；第三种方法是劳动密集型的，但可能更准确。帮助学生发展选择策略的想法。

例 9 在下列各行填入适当的数字、字母或数字，并解释原因。

【解说】启发学生探索规律。希望同学们体会：对于有规律的事物，无论是数字、字母还是图形，都可以体现出相同的规律，但表达方式不同。

示例 10 在图 1 中，追踪水平和垂直行上的两个数字相加为 10 的网格，然后追踪数字相加为 6 和 9 的网格。你能找到什么规律？

【解说】这个例子不仅可以帮助学生熟练地进行20以内的加法运算，还可以将数值与图形结合起来，有利于学生以后学习坐标系、图像等。

借助上图1，可以根据学生的实际情况提出不同的问题。例如，进一步画出两个数之和为8的网格，看看图案是什么。从上图来看，出现次数最多的总和是多少？最少的是什么？教师应根据学生的实际情况灵活设计教学。如果学生在观察上图或发现规律上有困难，教师可以引导学生从简单的情况开始，例如先将两个加数限制在 5 以内。

2011年版中小学数学新课程标准

2011年版中小学数学新课标：前言

2011年新中小学数学课程标准：课程目标

2011年版中小学数学新课程标准：学期目标

2011年新中小学数学课程标准：课程内容

2011年版中小学数学新课程标准：实施建议

2011年版中小学数学新课程标准：附录1

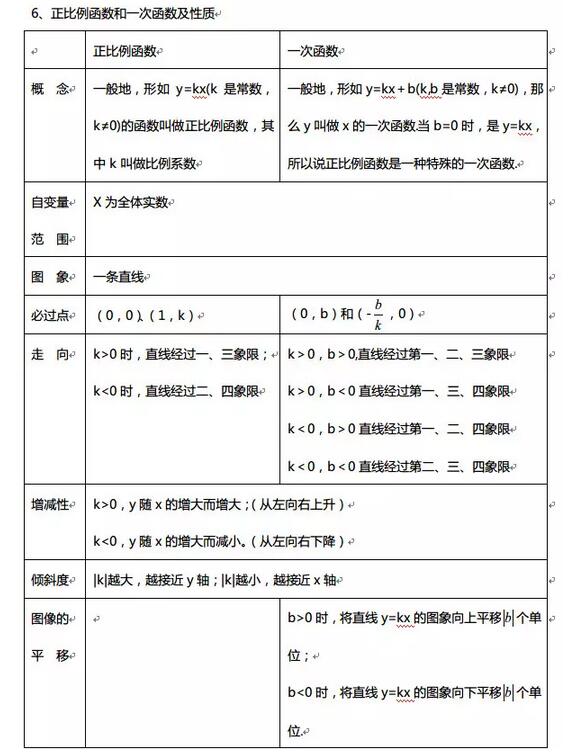
2011版中小学数学新课标：附录2（数与代数）

2011年版中小学数学新课程标准：附录2图形与几何

2011年版中小学数学新课程标准：附录2统计与概率

2011年版中小学数学新课程标准：附录2综合与实践

2011版中小学数学新课程标准：附录2第二节数与代数

2011年版中小学数学新课程标准：附录2二年级图形与几何

2011年版中小学数学新课程标准：附录2第二学期统计与概率

2011年版中小学数学新课程标准：附录2二年级综合与实践

欢迎来到 Olympus.com。您还可以通过手机等移动设备查询小学考试题库、小学资源库、小学新闻、重点中学、家庭教育信息等。2021年，我们一路相伴。>>[点击查看]

相关文章