等腰三角形知识点及典型习题教案模板3( 初三第一轮复习《三角形》教案及习题乘法口算100题)

第一轮第三轮复习《三角》教案及习题，乘法，口算，100题，七年级，有理数混合运算，100题，计算机一级题库，二元线性方程、应用题、真理或冒险、刺激性问题、新课标、三角形 1 理解三角形、内角、外角、中线、高角平分线的概念，画出任意三角形的角平分线、中线，高度理解三角形的稳定性。 2 探索和掌握三角形中线的性质。 3 理解全等三角形的概念。探索和掌握两个三角形。条件相等 4 了解等腰三角形的相关概念，探索和掌握等腰三角形的性质。等腰三角形的两个底角相等。高中心线与底边顶角的平分线为三线合一，三角形为等腰三角形。两个角相等的三角形是等腰三角形。了解等边三角形的概念并探索其性质。 5 了解直角三角形的概念，探索和掌握直角三角形的性质。三角形是有两个互补角的直角三角形。三角形是直角三角形。 6 在探索过程中体验勾股定理，运用勾股定理解决简单的问题，运用勾股定理的逆定理确定直角三角形图形并证明它关于三角形的部分 1 掌握以下基本事实作为证明依据 ①如果两个三角形和它们的角或两个角和它们的边或三个边分别相等，则这两个三角形全等 ②全等三角形的对应边分别相等。 2 用基本事实证明下列习题和考试中命题相关题的难度应等于所列命题的论证难度 ①三角形的内角与定理及其推论 外角三角形的内角等于两个不相邻的三角形的内角和外角大于任何一个不相邻的内角。 ②直角三角形全等定理。③角平分线性质定理和逆定理。三角形的三个角平分线相交于一点。 ④垂线平分线性质定理与逆定理三角形三边的垂线平分线相交于一点。 ⑤三角形的中线定理⑥等腰三角形等边三角形和直角三角形的性质

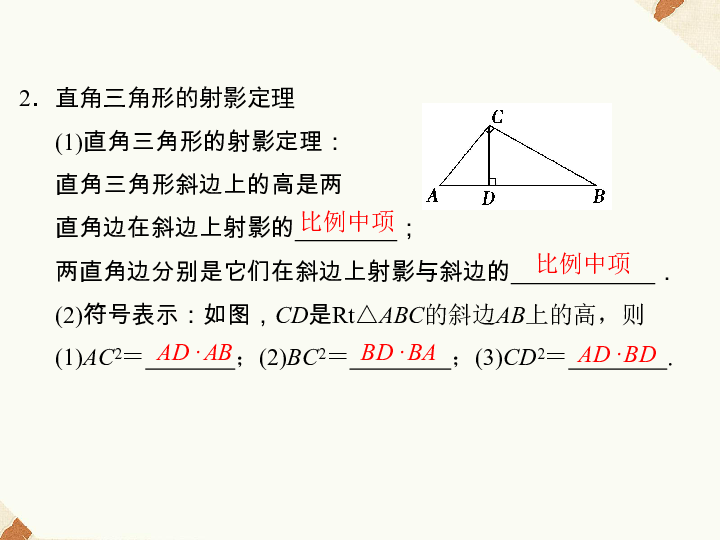
判断定理2知识网见《高考复习、精讲与考试》P67 三样题配知识点初中数学知识点总结七年级英语知识点七年级英语知识点总结人民教育版数学知识点初级一册一数学知识点三角形内角和定理及其推论12010河南103分。如图放置一个直角三角板，使30o角三角形的短直角边和45o角三角形的直角边重合，则∠1的度数为75o2 ，如右图所示。在图△ABC中，将∠A70o截断∠A，得到四边形BCDE。 ∠1∠2250o4附在习题上，考察三角形三边的关系。参见“高中入学考试复习与测试”P68。例 15 三角形的两条边分别为 49 和 3。如果边长为奇数，则第三边长为A3或5或7B5或7或9C7或9或11D9或11或136。四条线段长度为2cm3cm4cm5cm。取其中任意三个组成一个三角形。概率是知识点三角形是全等的。 12009河南179分如图∠BAC∠ABDACBD点O是ADBC的交点E是AB的中点试判断OE和AB的位置关系并给出证明OE⊥AB22008河南189分复习时全等三角形的知识，老师布置一道作业题如图①已知△ABC中，ABACP是△ABC中的任意一点。绕A点顺时针旋转AP到AQ∠QAP∠BAC连接到BQCP，那么BQCP小亮就是一个喜欢动脑筋的同学。他通过图①的分析证明△ABQ≌△ACP为了证明BQCP，他把点P移到等腰三角形ABC上。原题其他条件不变，发现BQCP依然成立。 P69 例题7 知识点 等腰三角形1 是△ABC 中的ABAC13BC10 和BC 边的中线AD。2 知道等边三角形的边长为4cm，其高等于cm。3 一等腰三角形的内角是另一个内角

内角的两倍，这个等腰三角形的三个内角是36o72o72o或45o45o90o4。如果等腰三角形两条边的长度是4和9，那么它的周长是225。如果比值是12，等腰三角形的顶角是150o或30o6。在△ABC中，ABACAB的垂直平分线与AC所在的线相交。锐角为30°。那么∠B60o或30o7就是等腰三角形ABC的ABACAC边上的中线BD。 △ABC的周长分为15cm和36cm两部分。求每边的长度 24cm24cm3cm8 见《中考复习与测试》 P70 第6题 知识点△ABC∠ACB90oACBCE中的直角三角形5是AC的上点，F是BC的上点 1点和ED⊥FD证明 EDFD6 如图 △ABC 和 △DBC ∠ACB∠DBC90oE 是 BC 的中点 DE⊥AB 在 F 处，ABDE1 证明△DBC 是等腰三角形 2 如果 BC8cm 求出 AC 的长度 7 如图线段BD和CE是△ABC的两个高度。 M是BC的中点。 N 是 DE 的中点。验证①MDME②连接MN，探索MN和DE之间的位置关系。如图8所示的四边形ABCD。∠ABC∠ADC90oM是BD的中点。证明MN⊥BD知识点三角形垂直平分线知识点三角形角平分线1为AC的中点，如Rt△ABC∠ACB90oBD平分线∠ABC在D点与AC相交等腰三角形知识点及典型习题教案模板3，AB4BD5为D点到BC点的距离为 32，如图 L1L2L3 表所示。党内积极分子人数与毫米对照表。教师职称等级列表。员工考核评分表。普通年金现值系数。如果它们相等，则有 4 3 个已知地址可供选择。 △ABC等腰三角形知识点及典型习题教案模板3，∠ABC与∠ACB的外角平分线在D点相交。证明AD平分∠BAC4如图∠

AOP∠BOP15oPC∥OAPD⊥OA 如右图为PC4cm，PD2cm5，在△ABC中，∠ABC的内角平分线与∠ACB的外角平分线相交于D点，BC的平行线相交AB 在 E 和 AC 之间的 F 点试图探索 EFBECF 之间的定量关系。知识点 三角形12010昆明的中线为113点。 DEF 的周长是 5cm2。 2006 广西有一个由三条中线围成的三角形。三角形的面积就是原三角形的面积。 3 如四边形ABCD所示，ABCDMNPQ是ADBCBDAC的中点。请判断线段MN和PQ之间的位置关系相互垂直。 4 如图，△ABC 中的AB12AC18AD 是∠BAC 过B 点的平分线，使AD 的垂线与AD 相交，DM 是BC 的中点，则MD 的长度为3 综合题1 如图等腰直角三角形 ABC O 是斜边 AC 的中点 P 是斜边 AC 上的移动点。 D是BC上的一点，PBPDDE⊥AC站在E点。证明1PEBO2设AC2APx四边形PBDE的面积为y。找出 y 和 x 关系之间的函数并写出函数的定义域。 2△ABC是等边三角形。点 D 是射线 BC 上的一个移动点。 D点与BC点不重合。△ABC是以AD为边的等边三角形。平行线的交叉点 E 作为 BC 连接到射线 ABAC 和点 FG。 BE1如图①所示，当D点在BC线段上时，试求△AEB≌△ADC，探究四边形BCGE如何是特殊四边形并说明原因。 2 如图②所示，当D点在BC线段的延长线上时直接写出1中的两个结论是否正确。 3 在2的情况下，当点D移动到四边形B的什么位置

CGE 是菱形并解释原因。第二个问题是第一个问题。图② 第二题和第一题3用尺子画出来。 AOB 平分线的方法如下。以O为圆心，任意长度为半径画圆弧 在CD处与OAOB相交，以CD点为圆心，半径大于EMBEDE等式3画圆弧，CD的长度为半径，两圆弧相交于点 P 作为射线 OP。 △OCP≌△ODP的基是ASASBASACAASDSSS3，如△ABC所示 ∠Aβ∠ABC的平分线与∠ACB的外平分线相交于A1∠A1BC的平分线与∠A1CB的外平分线相交于A点∠A1∠A2∠AnBCABAA1A2CDNDCMBAMQPDC 问题4 问题3 AB 有两条边，长度分别为3和5，第三条边为4或EMBEDE等式3.2 如图，D点是等腰直角ABC上的一点斜边 AB。绕C点逆时针旋转ACD，使其与BCD重合 则∠DBA_________度3①如右图所示，在△ABC∠ACB90oCD⊥AB中找到DBC3AC4中CD的长CD，EMBEDE等式3。②如△ABC中右图DAB8BD2中的∠ACB90oCD⊥AB求BC44的长CD如右图所示，△ABC中三角形∠ABC90°ABBC的顶点在三条平行线上，它们之间的距离为2，它们之间的距离为3。那么AC的长度就是 Question 6 Question 5 FFEEDDC

CBBAAAAABBBCCCDEOPPQQABOPDCEFDCBA 问题1 AABBCDDEEFFGG 问题2 图① 图② D′BDAC1 三角形三边垂直平分线的交点为三角形[来源主题A 垂直中心B 重心C 内心D 外心2 在Rt △ABC∠ACB90o∠ABC15oDE是AB的垂线平分线。垂直脚是D点E在BC上，那么AC8在同一条直线上。已知BCD点在同一条直线上。 △ABC 和△CDE 都是等边三角形。 BE 将AC 交给FAD 将CE 交给H ① 验证ADCE ② 验证CFCH ③ 判断CFH 的形状并说明原因

教案网123