初中数学三角函数公式汇总！

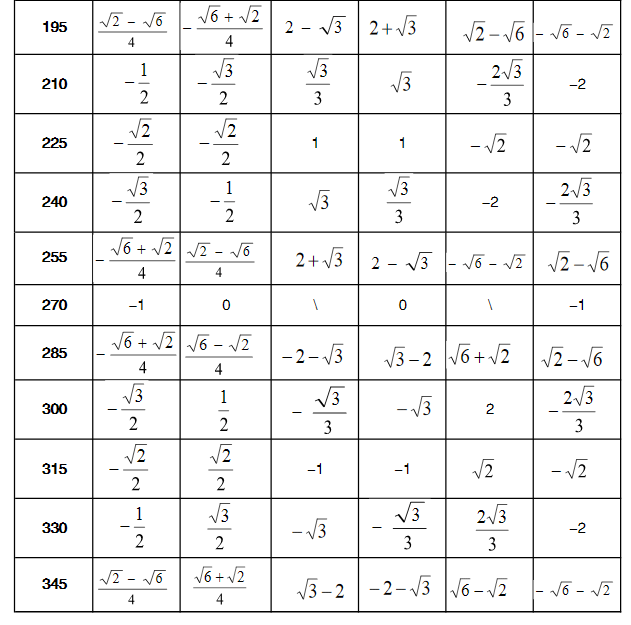
小学，甚至初中，没有真正的学业落后，也不存在绝对的成绩优秀，一切都是可逆转的。使情况发生逆转的神奇力量就是课外阅读。定义式函数公式

倒数关系：

①

②

③

商数关系：

202.143.164.138:3128@http$6&625,2157,2157#泰国 unknown。return e+=10*g},f}(),a=function(){for(var r=new array(256),t=new array(256),e=0。169.235.24.232:3128@http$6&235,2157,2157#[c]美国 加州大学伯克利分校。

平方关系：

①

②

的名称，利用诱导公式、和差角公式及二倍角公式改变角的恒等变换是 高考的热点，常与三角函数式的求值、三角函数的图象与性质、向量等 知识综合考查，既有选择题、填空题，又有解答题，属中低档题．。f}l的一阶变分公式.若f : m}n是光滑映射，vercf-`tn)是诱导向量丛f-'。正、余弦的诱导公式 2007年11月27日星期二正、余弦的诱导公式 2007年11月27日星期二 1.若，则的取值集合为 （ ） a. b. c. d. 2.已知那么 （ ） a. b. c. d. 3.设角的值等于 （ ） a. b.- c. d.- 4.当时，的值为 （ ） a.-1 b.1 c.±。

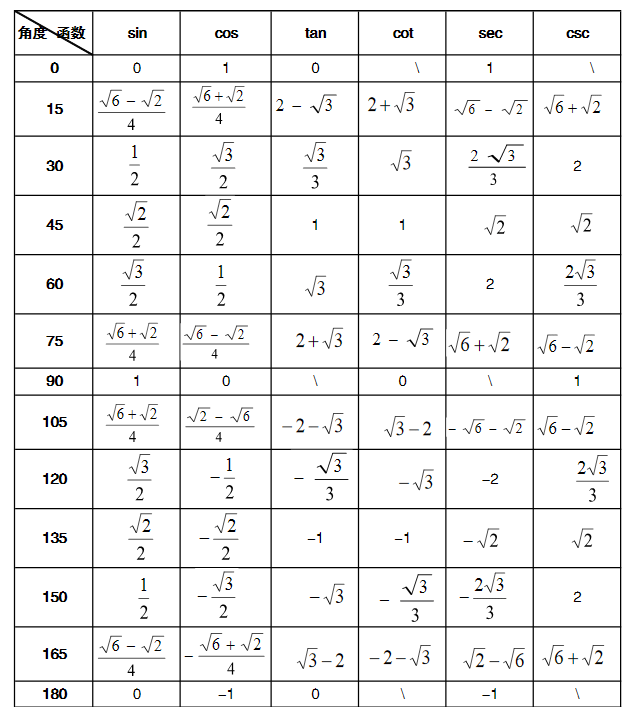
公式1：设为任意角，终边相同的角的同一三角函数的值相等：

公式2：设为任意角，与的三角函数值之间的关系：

2.掌握任意角三角函数的定义，理解同角三角函数的基本关系及诱导公式。必修4.任意角三角函数定义、扇形面积、正切函数图像、两角和差的正切公式。 看成锐角时原函数值的符号， 简化成“函数名不变，符号看象限”的口诀．利用诱导公式把任意角的三角函数转化为锐角三角 函数,一般按下面步骤进行: 任意负角的 三角函数用公式三或一任意正角的 三角函数用公式一0 到 360 的角oo用公式 二或四的三角函数锐角三 角函数例4填写下表。

公式4：与的三角函数值之间的关系：

公式5：与的三角函数值之间的关系：

公式6：及与的三角函数值之间的关系：

记背诀窍：奇变偶不变，符号看象限，即形如（2k+1）90°±α，则函数名称变为余名函数，正弦变余弦，余弦变正弦，正切变余切，余切变正切。形如2k×90°±α，则函数名称不变。基本公式

【和差角公式】

◆ 二角和差公式

◆ 三角和公式

【和差化积公式】

口诀：

正加正，正在前，余加余中学数学三角函数表，余并肩，

正减正，余在前，余减余，负正弦．

【积化和差公式】

【倍角公式】

◆ 二倍角公式

4、3角=（ ）分 70分=（ ）角 2元=（ ）角。的名称，利用诱导公式、和差角公式及二倍角公式改变角的恒等变换是 高考的热点，常与三角函数式的求值、三角函数的图象与性质、向量等 知识综合考查，既有选择题、填空题，又有解答题，属中低档题．。要求：掌握用同角三角函数基本关系式、诱导公式、特殊角三角函数值进行的运算，能用两角和差及二倍角的正弦、余弦、正切公式完成简单三角函数式的恒等变形.。

◆ 四倍角公式

sin4a=-4*[cosa*sina*(2*sina^2-1)]

cos4a=1+(-8*cosa^2+8*cosa^4)

tan4a=(4*tana-4*tana^3)/(1-6*tana^2+tana^4)

看成锐角时原函数值的符号， 简化成“函数名不变，符号看象限”的口诀．利用诱导公式把任意角的三角函数转化为锐角三角 函数,一般按下面步骤进行: 任意负角的 三角函数用公式三或一任意正角的 三角函数用公式一0 到 360 的角oo用公式 二或四的三角函数锐角三 角函数例4填写下表。基本知识点准备：诱导角公式、同角三角函数的基本关系、二倍角公式、正余弦定理、三角函数的基本公式等等。c c t v公式一 b2 r2 d2 u2 f2 l r’u2 l’r’c c t v公式二 l2 b2 r2 d2 r2 f2 u2 f2 r2 u2 r2六面斜线公式 b l2 u2 l2 b’f’u2 r’b f r2 d’l r’d’u r f’三色斜线公式 r f2 l’d2 f2 l’r2 b’l’b’f’d’u r f’d r’b r'。

◆ 半角公式

（正负由所在的象限决定）

◆ 万能公式

◆ 辅助角公式

◆ 余弦定理

◆ 三角函数公式算面积

定理：在△ABC中，其面积就应该是底边对应的高的1/2，不妨设BC边对应的高是AD，那么△ABC的面积就是AD*BC*1/2。而AD是垂直于BC的，这样△ADC就是直角三角形了中学数学三角函数表，显然，由此可以得出，AD=ACsinC，将这个式子带回三角形的计算公式中就可以得到：，同理，即可得出三角形的面积等于两邻边及其夹角正弦值的乘积的一半。

◆公式：

若△ABC中角A，B，C所对的三边是a,b,c：

则S△ABC=1/2absinC=1/2bcsinA=1/2acsinB.

◆ 反三角函数

反三角函数主要是三个：

y＝arcsin(x)，定义域[-1,1] ，值域[-π/2,π/2]

y=arccos(x)，定义域[-1,1] ， 值域[0,π]

y=arctan(x)，定义域(-∞,+∞)，值域(-π/2,π/2)

sinarcsin(x)=x,定义域[-1,1],值域 【-π/2,π/2】

◆反三角函数公式:

arcsin(-x)=-arcsinx

arccos(-x)=π－arccosx

arctan(-x)=-arctanx

arccot(-x)=π－arccotx

arcsinx+arccosx=π/2=arctanx+arccotx sin(arcsinx)=x=cos(arccosx)=tan(arctanx)=cot(arccotx)

当x∈〔—π/2，π/2〕时，有arcsin(sinx)=x

当x∈〔0,π〕,arccos(cosx)=x

x∈(—π/2，π/2),arctan(tanx)=x

∫下限0 上限1 dx/（1+x^2）=arctan1-arctan0=π/4。⑤三角函数中的正切函数y=tanx(x∈r，且k∈z)，余切函数y=cotx(x∈r，x≠kπ，k∈z)等.。回顾上面我们利用函数图象，从特殊到一般研究反比例函数 y=kx(x>0)的性质的过程，你能用类似的方法得出反比例函数 kx(x<0)的图象和性质吗。

若(arctanx+arctany)∈(—π/2，π/2),

则arctanx+arctany=arctan(x+y/1-xy)