等腰三角形知识点及典型习题教案模板3(《等腰三角形的性质》教学设计教学目标(一))
《等腰三角形的本质》教学设计
教学目标:
(一)教知识点
1.等腰三角形的概念。
2.等腰三角形的性质。
3.等腰三角形的概念和性质的应用。
(二)能力培训要求
1.体验制作(画)等腰三角形的过程,从轴对称的角度领略等腰三角形的特点。
2.探索和掌握等腰三角形的性质。
(三)情感和价值要求
通过学生的运算和思考,学生可以掌握等腰三角形的相关概念,培养在探索等腰三角形性质的过程中认真思考的习惯。
教学要点:
1.等腰三角形的概念和性质。
2.等腰三角形性质的应用。
教学难点:
等腰三角形三条线性质的理解与应用。
教学方法:
探索归纳。
教学过程:
一个。创造情境并介绍新课程
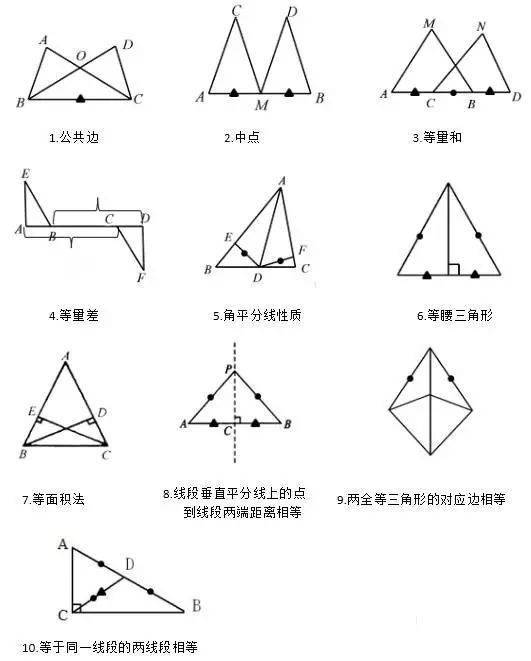
1、projection 展示几组图片;
2、student 观察并找到等腰三角形。
在之前的学习中,我们学习了轴对称图形,探索了轴对称的性质,能够将一个线对称图形做成一个简单的平面图形,并且通过轴对称变换我们能够设计出一些漂亮的形状。图案。在本课中,我们将从轴对称的角度认识一些熟悉的几何图形。在本课中,我们将认识一种轴对称三角形──等腰三角形。
两个。探索新知识
1. 做:如图:将一张长方形的纸按照图中的虚线对折,将红线下方的部分剪掉,然后展开得到△ABC .
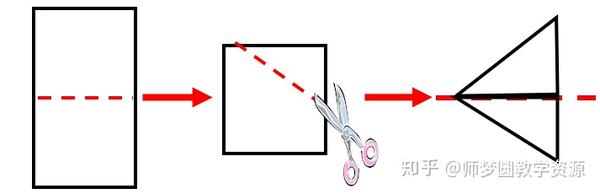
思考:AC和AB是什么关系?这个三角形是什么三角形?
回忆:(1)什么是等腰三角形?
(2)等腰三角形相关概念
(3)Triangle 学到了哪些重要的线段?
沿着折痕将切割的等腰三角形 ABC 对折以找到重叠的线段和角。
完成以下表格:

重合线段
重合角

重合线段
重合角
等腰三角形除了等腰外,你还能找到它的其他性质吗?
2. 猜猜:等腰三角形的两个底角相等。
已知:在△ABC中,AB=AC
验证:∠B=ÐC
分析:1.如何证明两个角相等?
2.如何构造两个全等三角形?
注意引导学生使用多种证明方法。
3.归纳:
性质1:等腰三角形的两个底角相等。 (等边等角)
申请格式:在△ABC中,
∵ AC=AB(已知)

∴∠B=∠C(等边等角)
4.练一练:
(1)如图,在下面的等腰三角形中,求它们底角的度数。
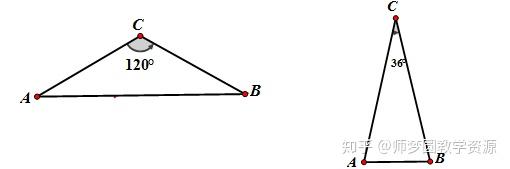
(2)等腰三角形底角为75°等腰三角形知识点及典型习题教案模板3,另外两个角为_____ __;
(3)等腰三角形一个角是70°,另外两个角是___________;
(4)等腰三角形的角是110°,另外两个角是________。
想一想:除了刚才的证明你可以得到∠B=∠C,你还能找到什么?
猜想:等腰三角形顶角平分线、底边中线、底边高重合
学生证。
总结:自然 2
等腰三角形顶角的平分线、底边的中线、底边的高重合。
申请格式:
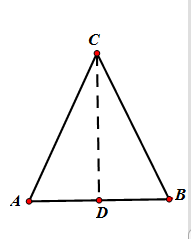
在△ABC中,AB=AC,D点在BC上
1、∵AD ⊥ BC

∴∠ = ∠, =.
2、∵AD为中线,
∴⊥,∠=∠。
3、∵AD 是角平分线,
∴⊥, =.
三、巩固练习:
1.Judgment:等腰三角形的角平分线、中线和高线相互重合。 ()
2.如图,AB=AC,AD⊥BC在D点与BC相交,BD=5cm,则BC的长度为
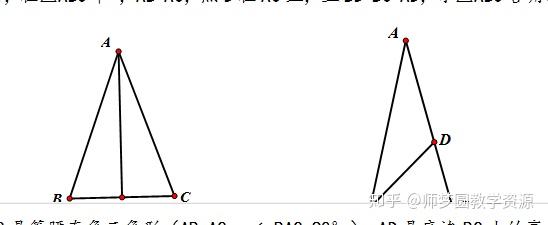
3.如图,在△ABC中,AB=AC,D点在AC上,BD=BC=AD,求△ABC各角的度数。
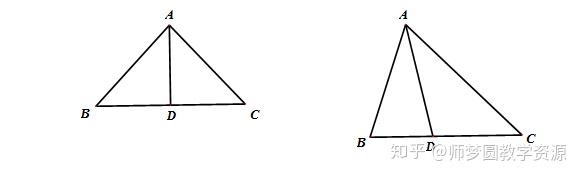
4.△ABC 是等腰直角三角形(AB=AC,∠BAC=90°),AD是底边BC上的高,记号∠B,∠C,∠BAD,∠DAC度数?
5.在△ABC中,AB=AD=DC,∠BAD=16°,求∠B和∠C的度数。
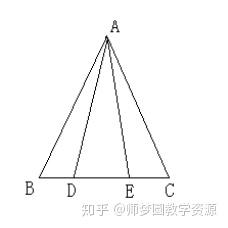
四、扩展练习:
(多解)如图,D点和E点在△ABC的BC边,AB=AC,AD=AE,此时BD和CE是什么关系?请解释原因。

五、小结:说说收获
性质1:等腰三角形的两个底角相等。 (等边等角)
性质2:等腰三角形的顶角平分线、底边的中线、底边的高重合。
这一课我们主要讨论了等腰三角形的性质,并对这些性质进行了简单的应用。等腰三角形是轴对称图形。它的两个底角相等(等边对等角)。等腰三角形的对称轴是其顶角的平分线,其顶角平分线都是底边的中线。 , 是底部的高度。通过本课,我们首先要了解和掌握这些性质,并能灵活运用。
六、课后作业
1.若△ABC为轴对称图形,其对称轴必为()
A.某一边的高度; B. 一侧中线
C.一条平分角和角的另一边的直线; D. 某个角度的平分线
2.等腰三角形的外角是100°,它的顶角是()
A. 80° B. 20° C. 80° 和 20° D。 80° 或 50°
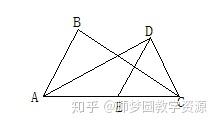
3.如右图所示,在△ABC中,过C为∠BAC的二等分线AD的垂线,垂足为D,DE∥AB过AC到E。
验证:AE=CE。
【教学反思】
等腰三角形作为特殊三角形的模型,不仅是对三角形和轴对称知识的深化,也是证明角相等、线段相等、直线相互垂直的共同依据。也是学习三角形类似三角形等的后续知识,打下扎实的基础。遗憾的是,由于等腰三角形的性质,这门课内容比较多,课容量大。在教学设计中,留给学生的时间和空间是一点点,让学生能够发现问题,但解决问题的时间太少。长期存在的“后遗症”是学生问题意识减弱。在探索关键问题时,我也缺乏提出想法的耐心和渴望。这是对学生的不信任,学生会在精神上变得懒惰。在教学实践中,提倡数学教学要更加关注学生的认知特点,力求让所有学生都能学到东西。本课从整体上看,学生基本掌握了等腰三角形“等边等角”和“三线合一”的性质等腰三角形知识点及典型习题教案模板3,学会了“等边等角”的应用,很好地完成了它们。教学目标。但是我还是觉得这样的上课方式并不能满足有较好学习基础的学生,会觉得自己不会吃饱。如果在课堂教学过程中尝试分组练习,整体的教学效果可能会更好。
教案网123
再个地方政府保护当地企业也很正常