初中数学人教2011课标版1-6年级数学版

杨少娟

地区：河南省-濮阳市-濮阳县

学校：河南省濮阳县城关镇第四中学

共1课时

13.3 等腰三角形初中数学人民教学2011年课程标准版

1 教学目标

知识目标：1、掌握等腰三角形的概念和性质。

2、 会用它的性质来证明和计算。

方法目标：分类讨论，一题多解，方程思维。

情感目标：培养学生的动手能力、概括能力和归纳能力，以及科学探究的精神。

2 重点和难点

关键点：等腰三角形的性质。

难点：等腰三角形性质的证明与应用。

3 教学过程3.1 第一堂课教学活动活动一【简介】创造情境点燃激情

1、让学生欣赏几张生活中的房子图片，让学生观察图片，老师问：图片中可以找到什么图形？

2、问起小学学过的等腰三角形的概念，老师重教。

3、师生一起回忆一般三角形的性质：1）三边关系定理

2），内角与定理

活动 2 [练习] 巩固和复习

问学生是否适合等腰三角形，下面的练习：

1、等腰三角形的腰围是3cm，底边是4cm，所以它的周长是；

2、等腰三角形一边长3cm，另一边长4cm，所以它的周长是；

3、一个等腰三角形的一边长3厘米，另一边长8厘米，所以它的周长是。

活动三【活动】分组讨论与合作探索

1、等腰三角形还有什么特殊性质？ （讲座题目、黑板题目）

2、自己动手

老师要求学生剪下 75 页教科书的纸，然后展开。可以看到什么图形？为方便回答问题，相同位置标有相同字母

思考：等腰三角形是轴对称图形吗？什么是对称轴？具体的折痕AD后面会在等腰三角形的名称中说明。

3、仔细观察、合作与交流

（1），提问：将切好的等腰三角形ABC沿折痕对折等腰三角形知识点及典型习题教案模板3，找到重叠的线段和角，填表，

大胆猜想：等腰三角形的两条腰围相等时，内角的性质是什么？

用文字描述：等腰三角形的两个底角相等。要求学生按照课文命题的证明过程写已知、验证、证明、画图。

通过团队合作与沟通

添加辅助线的三种方法：1)，作为顶点角的平分线AD，则∠BAD=∠CAD

2)，作为底部的中线AD，则BD=CD

3)，作为底部的高AD，则∠ADB=∠ADC=90°

对于每种方法，请找到一名团队成员来描述认证过程。这导致属性 1：

性质一：等腰三角形的两个底角相等（简称“等边等角”）

强调学生会用符号语言写作：

在△ABC中，

∵AC=AB（已知）

∴∠B=∠C（等边等角）

4、Exercise：1），一个等腰三角形底角为75°，另外两个角为

2)，等腰三角形的一个角是70°，另外两个角是

3），等腰三角形的一个角是110°，另外两个角是

5、再次回顾剪纸过程，重新观察填好的表格，从∠BAD=∠CAD，BD=CD，

∠ADB=∠ADC=90°得到属性2：

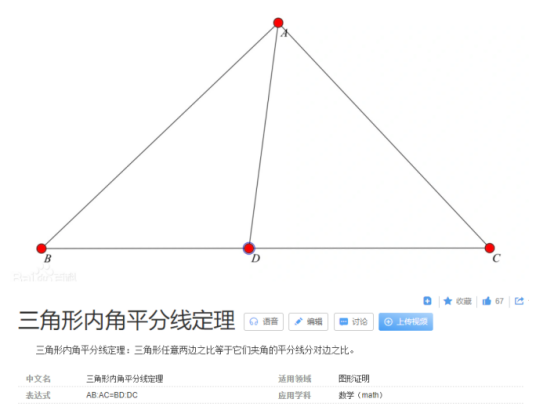
性质2：等腰三角形顶角平分线、底边中线、底边高重合（简称“三线合一”）

结合图形老师出题：在△ABC（1），若∠BAD=∠CAD，则----=---，---=---；

(2）, 如果BD=CD, 那么---=---, ---=---;

(3)，如果∠ADB=∠ADC=90°，则---=---，---=---。

此时，让学生回答等腰三角形的对称轴是什么？

活动四【讲座】用自然解决问题

例如如图（见课本），在△ABC中，AB=AC，D点在AC上，BD=BC=AD，求△ABC各角的度数。

解：∵AB=AC，BD=BC=AD，

∴∠ABC=∠C=∠BDC,∠A=∠ABD（等边等角）

设∠A=x，则∠BDC=∠A+∠ABD=2x

因此∠ABC=∠C=∠BDC=2x

所以在△ABC

是∠A+∠ABC+∠C=x+2x+2x=180°

已解决 x=36°

在△ABC中，∠A=36°，∠ABC=∠C=72°

（完成课前提出的问题，使本课前后呼应，成为一个整体。同时也是灵活运用自然2培养学生的应用意识）。

活动五【作业】总结总结

(五)谈谈你的收获

(六）归纳总结

(七）注重个性，布置作业

1、必做：教科书第77页，2、3题

2、精选题：课本第82页，4、6题

(八）板书设计13.3.1等腰三角形

一、definition 三、special nature

要素：腰、底边、顶角、底角1、是轴对称图形

二、1、具有一般三角形的性质：三边关系定理2、性1等边等角

内角与定理3、Property 2 三行合一

13.3 等腰三角形

课时设计课堂记录

13.3 等腰三角形

1 第一堂课教学活动活动一【简介】创造情境点燃激情

1、让学生欣赏几张生活中的房子图片，让学生观察图片，老师问：图片中可以找到什么图形？

2、问起小学学过的等腰三角形的概念，老师重教。

3、师生一起回忆一般三角形的性质：1）三边关系定理

2），内角与定理

活动 2 [练习] 巩固和复习

问学生是否适合等腰三角形等腰三角形知识点及典型习题教案模板3，下面的练习：

1、等腰三角形的腰围是3cm，底边是4cm，所以它的周长是；

2、等腰三角形一边长3cm，另一边长4cm，所以它的周长是；

3、一个等腰三角形的一边长3厘米，另一边长8厘米，所以它的周长是。

活动三【活动】分组讨论与合作探索

1、等腰三角形还有什么特殊性质？ （讲座题目、黑板题目）

2、自己动手

老师要求学生剪下 75 页教科书的纸，然后展开。可以看到什么图形？为方便回答问题，相同位置标有相同字母

思考：等腰三角形是轴对称图形吗？什么是对称轴？具体的折痕AD后面会在等腰三角形的名称中说明。

3、仔细观察、合作与交流

（1），提问：将切好的等腰三角形ABC沿折痕对折，找到重叠的线段和角，填表，

大胆猜想：等腰三角形的两条腰围相等时，内角的性质是什么？

用文字描述：等腰三角形的两个底角相等。要求学生按照课文命题的证明过程写已知、验证、证明、画图。

通过团队合作与沟通

添加辅助线的三种方法：1)，作为顶点角的平分线AD，则∠BAD=∠CAD

2)，作为底部的中线AD，则BD=CD

3)，作为底部的高AD，则∠ADB=∠ADC=90°

对于每种方法，请找到一名团队成员来描述认证过程。这导致属性 1：

性质一：等腰三角形的两个底角相等（简称“等边等角”）

强调学生会用符号语言写作：

在△ABC中，

∵AC=AB（已知）

∴∠B=∠C（等边等角）

4、Exercise：1），等腰三角形的一个底角是75°，另外两个底角是

2)，等腰三角形的一个角是70°，另外两个角是

3），等腰三角形的一个角是110°，另外两个角是

5、再次回顾剪纸过程，重新观察填好的表格，从∠BAD=∠CAD，BD=CD，

∠ADB=∠ADC=90°得到属性2：

性质2：等腰三角形的顶角平分线、底边的中线、底边的高重合（简称“三线合一”）

结合图形老师出题：在△ABC（1），若∠BAD=∠CAD，则----=---，---=---；

(2）, 如果BD=CD, 那么---=---, ---=---;

(3)，如果∠ADB=∠ADC=90°，则---=---，---=---。

此时，让学生回答等腰三角形的对称轴是什么？

活动四【讲座】用自然解决问题

例如如图（见课本），在△ABC中，AB=AC，D点在AC上，BD=BC=AD，求△ABC各角的度数。

解：∵AB=AC，BD=BC=AD，

∴∠ABC=∠C=∠BDC,∠A=∠ABD（等边等角）

设∠A=x，则∠BDC=∠A+∠ABD=2x

因此∠ABC=∠C=∠BDC=2x

所以在△ABC

是∠A+∠ABC+∠C=x+2x+2x=180°

已解决 x=36°

在△ABC中，∠A=36°，∠ABC=∠C=72°

（完成课前提出的问题，使本课前后呼应，成为一个整体。同时也是灵活运用自然2培养学生的应用意识）。

活动五【作业】总结总结

(五)谈谈你的收获

(六）归纳总结

(七）注重个性，布置作业

1、必做：教科书第77页，2、3题

2、精选题：课本第82页，4、6题

(八）板书设计13.3.1等腰三角形

一、definition 三、special nature

要素：腰、底边、顶角、底角1、是轴对称图形

二、1、具有一般三角形的性质：三边关系定理2、性1等边等角

内角与定理3、Property 2 三行合一

金玉涛