【初中英语】三角形及其有关概念,值得收藏!
一、三角形及其有关概念
1、三角形:由不在同一直线上的三条线段首尾顺次相接所构成的图形叫做三角形。组成三角形的直线叫做三角形的边;相邻两边的公共交点叫做三角形的顶点;相邻两边所构成的角也称三角形的顶角,简称三角形的角。
2、三角形的表示:三角形用符号“Δ”表示,顶点是A、B、C的三角形记作“ΔABC”,读作“三角形ABC”。
3、三角形的三边关系:
(1)三角形任意两边之跟大于第三边。
(2)三角形任意两边之差大于第三边。(三角形的第三边大于两侧之差高于两边之跟)
(3)作用:①判断三条已知直线是否构成三角形②当已知两边时,可确认第三边的范围。③证明线段不等关系。
(4)①一般地,对于三角形的某一条边a来说,一定有|b-c|<a<b+c成立;反之,只有|b-c|<a<b+c成立,a、b、c三条线段才能组成三角形;②特殊地,如果已知线段a最大,只要满足b+c>a,那么a、b、c三条线段就能组成三角形;如果已知直线a最小,只要满足|b-c|<a,那么这三条线段就能构成三角形。
4、三角形的内角的关系:
(1)三角形三个内角和等于180°(2)直角三角形的两个锐角互余。
5、三角形的稳定性:三角形的外形是固定的,三角形的这个性质叫做三角形的稳定性。四边形具有不稳定性。
6、三角形的分类:
(1)三角形按边分类:
不等边三角形
三角形 底和腰不相等的直角三角形
等腰三角形
等边三角形,也叫正三角形。
(2)三角形按角分类:

直角三角形(有一个角为直角的三角形)
三角形 锐角三角形(三个角都是锐角的三角形)
斜三角形
钝角三角形(有一个角为钝角的三角形)
把边和角联系在一起,我们既有一种特殊的三角形:等腰直角三角形。它是两条直角边相等的等腰三角形。
7、三角形的三种重要线段:
(1)三角形的中线:
定义:在三角形中,连接一个顶点和它对边的中点的直线叫做三角形的中线。
性质:三角形的三条中线交于一点(重心),交点在三角形的内部。
(2)三角形的角平分线:
定义:在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与端点之间的垂线叫做三角形的角平分线。
性质:三角形的三条角平分线交于一点(内心)。交点在三角形的内部。
(3)三角形的高线:
定义:从三角形一个顶点向它的对边所在线段作切线,顶点和垂足之间的垂线叫做三角形的高线(简称三角形的高)。
性质:三角形的三条高所在的线段交于一点(垂心)。锐角三角形的三条高线的端点在它的外部;直角三角形的三条高线的端点是它的底边的中点;钝角三角形的三条高所在的直线的交点在它的内部;
区别

相同
中线
平分对边
三条中线交于三角形内部
(1)都是线段(2)都从顶点画出(3)所在直线相交于一点
角平分线
平分内角
三条角平分线交于三角表内部
高线
垂直于对边(或其延长线)
锐角三角形:三条高线都在三角形内部
直角三角形:其中两条恰好是直角边
二、图形的全等
全等图形:定义:能够完全重叠的两个图形叫做全等图形。性质:全等图形的颜色跟大小都同样。
1、全等三角形及有关概念:
能够完全重叠的两个三角形叫做全等三角形。两个三角形全等时,互相重叠的顶点叫做对应顶点,互相重叠的边叫做对应边,互相重叠的角叫做对应角。
2、全等三角形的表示:
全等用符号“≌”表示,读作“全等于”。如△ABC≌△DEF,读作“三角形ABC全等于三角形DEF”。
注意:记两个全等三角形时,通常把表示对应顶点的字母写在对应的位置上。
3、全等三角形的性质:全等三角形的对应边相同等腰三角形知识点及典型习题教案模板3,对应角相等。
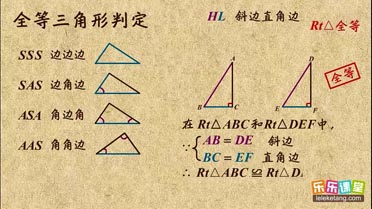
4、三角形全等的判定:
(1)边边边:有三边对应相同的两个三角形全等(可缩写成“边边边”或“SSS”)。
(2)角边角:两角及其夹边对应相同的两个三角形全等(可简写成“角边角”或“ASA”)
(3)角角边:两角分别相同且其中一组等角的对边相同的两个三角形全等(可缩写成“角角边”或“AAS”)
(4)边角边:两边以及夹角分别相同的两个三角形全等(可缩写成“边角边”或“SAS”)
5.注意:①判定两个三角形全等必须有一组边对应相同; ②全等三角形面积相等.
6、用尺规做三角形(依据判断)“SAS”“ASA”“SSS”
题目:已知三边作三角形。
已知:如图,线段a,b,c.
求作:△ABC等腰三角形知识点及典型习题教案模板3,使AB = c,AC = b,BC = a.
作法:

(1)作线段AB=c;
(2)以A为圆心b为直径作弧,
(3)以B为圆心a为直径作弧与前弧相交于C;
(4)连接AC,BC。
则△ABC就是所求作的三角形。
题目二:已知两边及夹角作三角形。
已知:如图,线段m,n, ∠α.
求作:△ABC,使∠A=∠α,AB=m,AC=n.
作法:
(1)作∠A=∠α;
(2)在AB上截取AB=m ,AC=n;
(3)连接BC。
则△ABC就是所求作的三角形。
题目三:已知两角及夹边作三角形。
已知:如图,∠α,∠β,线段m .
求作:△ABC,使∠A=∠α,∠B=∠β,AB=m.

作法:
(1)作线段AB=m;
(2)在AB的同旁作∠A=∠α,作∠B=∠β,
∠A与∠B的另一边相交于C。
则△ABC就是所求作的图形(三角形)。
作图题的一般步骤:
(1)已知,即将条件具体化;
(2)求作,即具体描述所作图-+形应满足的条件;
(3)分析,即寻求作图步骤的方法(通常是画出草图);
(4)作法,即依据预测所得的作图步骤,作出正式图形,并依次叙述作图过程;
(5)证明,即验证所作图形的正确性(通常省略不写)。
7、利用三角形全等测距离
1、利用三角形全等测距离,实际上是运用已有的全等三角形,或构造出全等三角形,运用全等三角形的性质(对应边相同),把较难测量或难以测量的距离转换成已知直线或较易于判读的直线的厚度,从而受到被测距离。
2、运用全等三角形解决实际问题的方法:
(1)先确立实际问题需要用这些几何知道解决;
(2)根据实际问题抽象出几何图形;
(3)结合图形跟题意分析已知条件;
(4)找到解决难题的方式。
果断刷机了