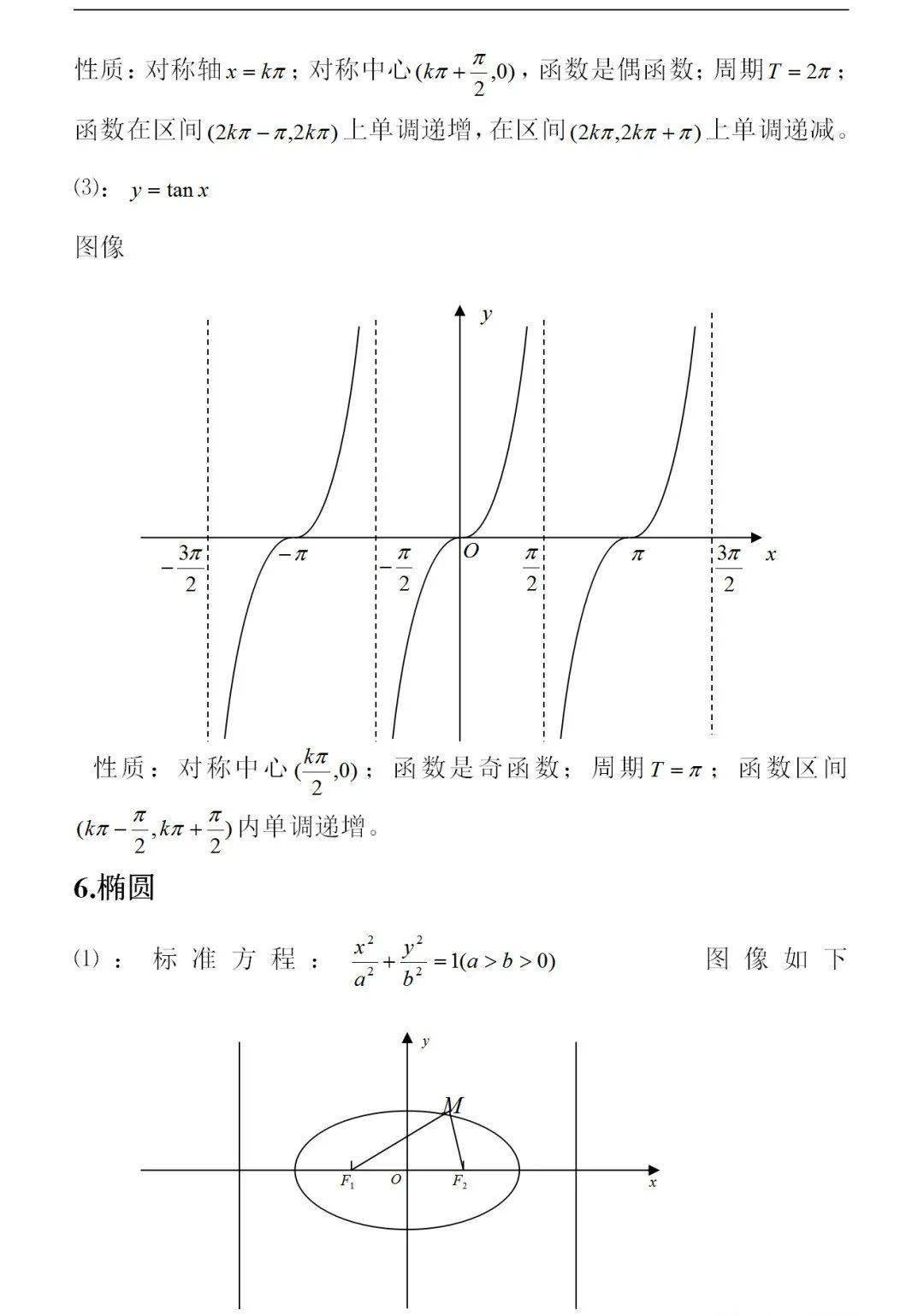
掌握一次函数教案，让学生更上手

在学习数学的过程中，一次函数是我们接触的第一个函数类型。然而，如何让学生更好地掌握一次函数的知识呢？本文以亲身经历为基础，分享了一份针对初中生的一次函数教案格式。以下将从教案目标、教学重点、难点分析、课前预习等方面逐步介绍这份教案。

1.教案目标

通过本节课的学习，学生应该能够：

-理解什么是一次函数；

-掌握一次函数的基本概念；

-能够根据实际问题建立一次函数模型；

-熟练掌握一次函数图像的画法和性质。

2.教学重点

-了解一次函数的定义和性质；

-掌握一次函数图像的特征和画法；

-学会如何根据实际问题建立一次函数模型。

3.难点分析

-对于初中生而言，理解“函数”的概念可能比较抽象，需要耐心引导；

-对于不同难度的题目，建立合适的数学模型也需要进行分层引导。

4.课前预习

在开始上课前，老师可以通过以下方式引导学生进行预习：

-阅读一次函数基本概念的相关知识点；

-尝试画出一次函数图像并探讨其性质；

-查阅相关实际问题，思考如何建立对应的一次函数模型。

5.课堂教学

5.1引入新知

通过展示一些实际问题，引导学生思考如何用数学模型来解决这些问题。例如：“如果你去超市购物，每瓶可乐售价2元，那么你需要花多少钱才能买到10瓶可乐？”这个问题可以引出一次函数的概念。

5.2概念讲解

在引入新知之后，老师可以对一次函数的定义和性质进行详细讲解。具体内容包括：

-什么是一次函数；

-一次函数的定义和表达式；

-一次函数的图像和性质。

5.3图像绘制

接下来，老师可以通过绘制一次函数的图像来加深学生对其性质的理解。老师可以从以下几个方面进行讲解：

-如何确定图像的斜率和截距；

-如何绘制图像，并探讨其性质。

5.4模型建立

在学习了一次函数的基本概念之后，老师可以通过一些实际问题来引导学生建立对应的数学模型。例如：“如果你每天花费1元钱乘坐公交车，那么一个月需要花多少钱？”这个问题可以引出建立一次函数模型的方法。

5.5练习题目

最后，老师可以通过一些练习题目来检验学生对于一次函数的掌握程度。练习题目可以包括：

-填空题：已知函数f(x)=2x+1，则f(3)=______；

-计算题：如果y=3x+5，求当x=2时y的值；

-应用题：某公司销售部门销售额为200万元/年，每增加一个销售员，销售额可增加10万元/年，那么至少要增加几个销售员才能达到250万元/年？

6.总结反思

通过本节课的学习，学生能够更好地理解一次函数的概念和性质，并掌握了如何根据实际问题建立对应的数学模型。同时，在教学过程中，老师也需要不断反思和总结，不断优化教学方法，以提高教学效果。