事业单位考试公共基础知识：变量与函数(1)

变量与数组(1)备课日期上课日期课型：新授 主备人：宋以美学习目标①运用丰富的例子,使学生在准确情境中体会函数概念的涵义,了解常量与函数的涵义。能分清实例中的常量与数组,了解自变量与变量的涵义。②通过动手实践与构建,让学生参加变量的看到跟函数概念的产生过程,以提升预测问题跟解决难题的素养。③引导学员探索实际问题中的数量关系,培养对学习英语的兴趣跟积极参加英语活动的热情.在缓解问题的过程中感受数学的应用价值并展现成功的愉悦,建立自信心。学习重点与瓶颈重点：函数概念的产生过程。难点：正确理解变量的概念。学习过程：学习活动（一）：提出问题:1.汽车以60千米/时的速率匀速行驶。行驶里程为s千米,行驶时间为t小时。先填写下面的表,再试着用含t的式子表示s：t(小时)12345s(千米)2.已知每张电影票的价格为10元。如果早场售出150张,日场售出205张,晚场售出310张,那么三场电影的收视收入各为多少元?设一场电影售出x张票,票房收人为y元,怎样用含x的式子表示y?_________________________3.要画一个面积为10cm2的圆,圆的半径要取多少?画面积为20cm2的圆呢?怎样用含圆面积S的式子表示圆半径r?学习活动（二）：动手实验(分组进行试验活动,然后各组选派代表汇报)。

1.在一根弹簧秤上悬挂重物,改变并记录物体的质量,观察并记录弹簧长度的差异,填入下表：悬挂重物的质量m(kg)弹簧尺寸l(cm)如果弹簧原长10cm,每1kg重物使弹簧伸长0.5cm,怎样用物体质量m(kg)的式子表示受力后的弹簧尺寸l(cm)?____________________________2.用10dm长的铁丝围成圆形.试改变方形的长,观察矩形的面积如何变迁,记录不同的矩形的长的值,计算相应的矩形面积的值,探索他们的差异规律(用表格表示) 。设矩形的长为xdm,面积为Sdm2,怎样用含x的式子表示S?_______________________________________学习活动（三）探究新知(一)变量与常量的概念1.在动手实验并充分发表自己看法的基础上,归纳：上面的难题和实验都体现了不同事物的差异过程。其中有些量__________的值是根据某些规律差异的。在一个变化过程中,数值出现差异的量,我们称之为_________。也有些量是一直不变的,如前面问题中的速度60(千米/时)、票价10(元)等,我们称之为______________。2.请详细指出里面那些问题跟实验中,哪些量是函数,哪些量是常量。

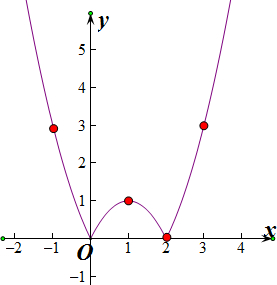
3.举出一些差异的例子,指出其中的函数跟常量。(二)函数的概念1：上面的每个问题跟实验中的两个变量相互_______.当其中一个变量取定一个值时,另一个变量就有_____________________。2.一般来说,在一个变化过程中,如果有两个变量x与y,并且针对____的每一个确定的值,___都有唯一确认的值与其对应,那么,我们就说___是自变量,___是x的变量。如果当x=a时,y=b,那么,_____叫做当自变量的值为______时的____。例如在问题1中,时间______是自变量,里程____是______的变量。t=1时,其函数值s为60,t=2时,其函数值s为120。3、在心电图中,时间_____是自变量,心脏电流____是_____的变量；在人口统计表中,年份___是自变量,人口数_____是______的变量.当x=1999时,函数值y=_______巩固新知下列各题中分别有几个变量?你可将其中的某个变量看成是另一变量的函数吗?1.右图是北京某日温度变化图2.如图,已知菱形ABCD的对角线AC长为4,BD的长在变化,设BD的长为x,则矩形的面积为y=×4×x 3.国内平信邮资(外埠,100克内)简表：信件质量m/克O0)的图像,可以看出曲线从左向右增长,即当x由小变大时, y=随之增加.(2) 归纳用描点法画函数图像的通常方法.描点法画函数图像的通常方法如下：第一步：列表；(表中给出一些自变量的值以及对应的函数值)第二步：描点；(在直角坐标系中,以自变量的值为横坐标,相应的变量值为纵坐标,描出表格中数值对应的各点)第三步：连线.(按照横坐标由小到大的次序,把所描出的各点用平滑的曲线连接出来)讨论交流:教科书P.115 “思考”中的两个问题.巩固新知1.画出变量y=2x-1的图象.判断：点A(-2.5,-4)、点B(1,3)、点C(2.5,4)是否在变量y=2x-1的图象上.2.画出变量y=x2的图像.从图象中观察,当x0时呢?注:理解用图象法表示方程关系.巩固函数图像的技法.总结归纳以难题的方式要求学员思考、交流：1.作变量图象的三个步骤分别是哪个?2.如何从图像中认识函数的差异情况?注:加深对函数图像画法的印象.布置作业1.必做题：教科书P.119 第6题.2.选做题：教科书P.120 第10题.教学反思 14.1变量与函数(5)教学目标①运用丰富的例子,帮助学生全面理解变量的三种表示方式.②通过观察、作图、交流、归纳等物理实践活动,使学员加深对函数三种表示方式的了解,提高把实际问题转换为数学难题的素养.③让学员通过实际操作,体会函数的三种表示方式在实际生活中的应用价值,以促使教师对物理的学习兴趣.教学重点与难点重点：函数的三种表示方式以及应用.难点：函数的三种表示方式的应用.教学准备纸板一块、玩具汽车一辆、三角尺、CAI课件.教学设计强调问题实验演示：倾斜木板,将小车置于木板顶端,观察汽车下滑过程.小车沿斜坡下降,下滑速率与其增长时间的关系如上图所示.1.填写下表：t(秒)123V(米/秒)2.写出V与t之间的关系式.注:通过试验演示,创设问题情境,使教师从中发现数学,建立建模,引起思考,激发兴趣.营造轻松愉快的学习气氛,自然导入新课.探究新知1.通过学习,我们将要知道可以用列表格、写式子和画讨论：从后面的事例来看,你觉得这三种表示方式各有哪些优点?注:分组活动.先独立探讨,然后组内交流并作记录,最后各组选派代表汇报. 2.注意：表示函数时,要按照详细状况选择适当的方式.图象的技巧来表示变量.这三种表示数组的方式分别被称为列表法、解析式法跟图象法.为了全面地了解问题,有时需要几种方法同时利用. 讲解教科书P.117 例4.问题1：观察记录表中的6组数值,你觉得这两个变量之间有哪些关系?问题2：请你写出水位高度y(米)随时间t(时)变化的函数解析式.问题3：请你画出这个变量的图像.问题4：请你预测一下,再过2小时,水位高度将超过多少米?注:给学生提供充分的时间与空间,让其进行自主探索和与同伴交流,经历数学活动的过程.学生的探求可能带有盲目性,精心设计“问题串”可帮助缓解这个难题.但它不能代替学生的探索,而是为学生的构建提供指导.一切应从有利于学生的演进出发.巩固新知教科书P.118 练习第1、2题注:加深对变量三种表示方式的理解.解决难题某电视机厂要印制一批产品宣传资料.甲厂提出：每份资料收1元印制费,所有资料另收1500元的制版费；乙厂提出：每份资料收2.5元印制费,不收制版费.1.分别写出两厂的收费y(元)与印制数量x(份)之间的关系式.2.在同一直角坐标系内做出他们的图像.3.根据图象回答下面问题：(1)印制800份宣传资料,选择哪个印刷厂比较合算?(2)电视机厂拟拿出3000元用于印制宣传资料,选择哪个印刷厂宣传资料可多印一些?注:感受所学知识在实际中的功能,培养教师应用物理的观念. 总结归纳教师指出,本节课主要学习了函数的三种表示方式：列表法、解析式法跟图象法以及各自的特点.特别提示：函数的不同表示方式之间是可以转换的.注:引导学员归纳总结所学知识,使之对函数的表示方式有相当全面的了解.布置作业1.必做题：教科书P.120 第11题.教学反思 14.2.1正比例函数教学目标①通过对不同背景下方程建模(关系式)的相当,接受正比例函数的概念.②在用描点法画正比例函数图象的过程中看到正比例函数的性质.③利用发现的性质简便地画出正比例函数的图像.④初步体验研究变量的通常模式与技巧.教学重点与难点重点:正比例函数的概念、图象与性质.难点：体验研究变量的通常模式与技巧教学准备学生准备：作图工具、多媒体课件.学生准备：作图工具、方格子纸若干张.教学设计概念的引出1.出示教科书P.122 的疑问.先出示问题背景,再逐一提出问题①、②、③.注:问题的解决可由一位学生提问,其他学生补充进行.说明：以上我们用变量y=200x对燕鸥的飞行路程问题进行了刻画.尽管这并非近似的,但它可以成为体现燕鸥的行程与时间的对应规律的一个模型.注:此问题源于真实背景,难度又不大,在让全体学员进入学习状况的同时,也进一步体会到函数是体现现实世界的一种数学建模.2.此类模型在生活中广泛存在.出示教科书P.23 的问题：下列问题中的变量对应规律可用怎样的变量表示?这些函数有哪些共同点?注:在差异的背景中寻求不变之处,经历对一类对象共同本质特性的具象过程,促进概念的产生.通过探讨、归纳形成议题,给出正比例函数的概念.一般地,形如y=kx(k是系数,k≠O)的方程,叫做正比例函数,其中k叫做比例系数.注:这里不补充正反例的非常来进行概念的辨析,这部分内容放在下一节. 上述问题中各正比例函数的比重系数分别是哪个?注:认识的扩大.我们了解,函数图像可以直观、清晰地表示方程关系.正比例函数的解析式具有共同的构架,那么他们的图象是否还有某些必然的一同之处呢？1.画出以下正比例函数的图像：(1)y=2x(2)y=-2x学生通过列表、描点、连线画出图像,使用课前打算好的方格子纸(或由教师统一发下)可以节省时间缩短效率.注:自然促使探究冲动,感受研究函数的探讨方式.利用已学过的描点法画出正比例函数的图像,既巩固旧知识,更为发现规律后简便画法的形成埋下伏笔.2.比较后面两个函数的图像的相似点与不同点,你看到他们具有怎么的规律了吗?注:让学生充分发表看法,鼓励百家争鸣、各抒己见,教师暂时不做评判,对于争论最好的方法是使学生自己想办法验证解决.学生经历活动操作、观察非常、分析探讨、讨论交流的过程,并在这种一个过程中确立信心、获取知识、体验学习的方式.引导学员思考：这种规律对其它正比例函数适用吗?具有一般规律吗?3.适时引导学生再次尝试：练习：在同一个坐标系中,画出以下函数的图像,并对他们进行非常：(1)y=x(2)y=-x注:(1)这里无须就k=O时既如何展开争论,若有学生谈到,可引导在课外思考.(2)量的累积可以进一步提高信心,明确经验,有助于对各类意见的统一认识的全面定型.4.达成共识：一般地,正比例函数y=kx(k≠0)的图象是一条经过原点的直线,我们称它为直线y=kx.当k>0时,直线y=kx经过第三、一象限,从左向右上升,即随着x的减小y也减少；当k0时,向上平移；当b0时,y随x的减小而减少；当k0②当x为何值时,函数y=2x-4的值小于0?此处对教科书上引例稍作改变,让学生顺着上节课的认知,用类似的看法处理不等式问题.(2)你怎么运用图象来表明②?(师生对以上两个问题一起议论,一起得出结论)注:当y取值从上节课的等于0变成了这节课的小于0,相应的x值也由一个定值变成一个范围；如何在图象上看,对学生来说需要认知的跳跃.(3)“解不等式2x-40或ax+b0,0的解集是x3；-x+3≥0的解集是x≤3；-x+3≤0的解是x≥32.如上图,利用y=-x+5的图象,(1)求出-x+5=0的解；(2)求出-x+5>0的解集；(3)求出-x+5≤0的解集(4)你可求出-x+5>3的解集吗?(5)你能够求出这些不等式的解集呢?解：(略)注:第2题同样是突出本节课重点内容的一种设计.(4)(5)小题为拓展开放.小结反思通过以上的剖析和训练,我们了解,对于通常的一元一次不等式ax+6>0,它与一次函数的方程、利用图像分析数量关系等弊端关系更紧密.具体见如下框图：从数的角度看：求ax+b>0(a≠0)的解x为何值时y=ax+b的值小于0从形的角度看：求ax+b>0(a≠0)的解确定直线y=ax+b在x轴上面的图像所对应的x值针对0的解；(3)若-1≤y≤3，求x的取值范围.(此题意在考查一次函数与一元一次方程和一元一次不等式(组).) 13.(10分)小强骑自行车去游玩，右图表示他离家的距离.y(千米)与所用的时间t(小时)之间关系的变量图象，小明9点离开家，15点回家，根据这个图象，请你回答以下问题：(1)小强到离家最远的地方需几小时?此时离家多远?(2)何时开始第一次休息?休息时间多长?(3)小强何时距家21km?(写出计算过程)(此题意在考查学生运用函数图像解决实际问题的能力及识图能力.)14.(12分)网络时代的到来，很多家庭都接入了网路，电信局规定了拨号入网两种收费模式一次函数教案格式，用户可以任选其一：A：计时制：O.05元/分； B：全月制：54元/月(限一部个人住宅电话入网).此外B种上网模式要加收通信费0.02元/分.(1)某用户某月上网的时间为x小时，两种收费模式的成本分别为y1(元)、y2(元)，写出y1、y2与x之间的方程关系式.(2)在上网时间同样的条件下，请你给该客户选择那种方法上网更省钱?(此题意在考查一次函数与二元一次方程组.) 15.(12分)某服装厂现有A种布料70m，B种布料52m，现计划用这两种布料制造M、N两种款式的服装80套.已知做一套M型号的服装必须A种面料0.6m，B种布料O.9m，可获利45元，做一套N型号的服装必须A种布料1.1m，B种布料0.4m，可获利50元.若设生产N型号的服装套数为x，用这批布料制造这两种款式的服装所获的总收入为y元.(1)求y与x的方程关系式，并求出自变量x的取值范围；(2)该服装厂在制造这批服装中，当制造N型号的服装多少套时，所获利润最大?最大利润是多少?(此题意在考查一次函数在解最大(小)值问题中的应用.) 四、附加题(此大题满分20分)：16.如图，直线y=kx+6与x轴y轴分别交于点E，F.点E的坐标为(-8，0)，点A的坐标为(-6，0).(1)求k的值；(2)若点P(x，y)是第二象限内的直线上的一个动点一次函数教案格式，当点P运动过程中，试写出△OPA的面积S与x的方程关系式，并写出自变量x的取值范围；(3)探究：当P运动至哪个位置时，△OPA的面积为，并表明理由.(此题意在考查数形结合能力及坐标几何难题的综合应用.) 教学反思