【数学】一次函数与一元一次不等式的辩证关系

一次函数与一元一次不等式教学设计 教 学 内 新人教版义务教育课程标准实验教科书《数学》八年级上册。 容 1. 使学生领会一次函数与一元一次方程、一元一次不等式之间的联系。 教 2. 引导学生经历探究一次函数与一元一次方程、一元一次不等式之间的联系的过程，体会数形结合、分类、 学 类比、归纳等物理观念方法的利用，积累数学活动心得。通过自主研究、小组合作等活动，锻炼学生的 目 自学能力、归纳概括的素养，增强教师间的合作观念。 标 3. 通过对一次函数、一次方程与一元一次不等式内在关系的探讨，引导学生了解事物部分与整体的辩证统 一关系，培养学生用联系的看法看待数学难题的观念。 函数、方程、不等式都是人们刻画现实世界的重要物理建模。之前，学生即将从数的视角认 识一次方程和一次不等式，从形的视角认识了一次方程和数轴表示不等式的解集。而本节课通过 函数图像动态的差异跟点的对应来探究一次函数、一元一次方程、一元一次不等式之间的关系。 通过本节课的探讨，学生除了可加深对变量、方程（组）、不等式的理解一次函数教案格式，而且可在函数的观点 下将两者统一起来，感受数学的统一美，加强知识间横向与纵向的融会贯通。

一次函数、一元一 教 次函数、一元一次不等式之间的关系属于事实性知识；学生在研究三个一次之间关系的过程中， 内容解读 材 需要在变量运动变化的看法下，经历运用分类、类比一次函数教案格式，数形结合的观念方法，归纳出解一次方程 分 和不等式的难题，其实是求函数的零点和非零点的弊端，这些思维策略可有效地帮助学员积累数 析 学活动心得，掌握学习方法，提高学习效率，因此，这些物理观念方法是元认知知识。 本节课将“三个一次”问题在函数的看法下来集中了解，这种用整体的看法处理难题的方 法为日后学习二次函数与一元二次方程的关系，以及高中二次函数、一元二次方程与一元二次不 等式的常识做好知识跟认知方式上的打算。 教学重点 探究一次函数与一元一次方程、一元一次不等式之间内在关系。 教学难点 对一次函数与一元一次方程、一元一次不等式之间关系的阐述。 1．之前，学生即将会解一次方程和一次不等式，从形的视角认识了一次方程的图像跟在数轴上表示不等式 学 的解集，学生具备了接受这节课的知识基础。 情 2． 八年级学生的认知已逐渐从直观的形象思维为主向写实的逻辑思维过渡，而且具有一定的图像分析跟 分 信息收集的能力。

但是因为所学知识是零散的，数跟形没有形成有意识的联系，学生无法确立一次函数与 析 一次方程、一次不等式之间的联系，因此，“三个一次”之间的关系的阐述是本节课的症结。如何创设问题， 引导学生用联系的看法进行研究，是突破瓶颈的关键。 通过以上预测，教学中将采取以下教学思路： 1．创设实际生活情境，鼓励教师多向探讨、多角度解决实际问题，引导学生初步感受一元一次不等式与一 元一次函数、一次函数是有联系的。 教 2．从教师未会的解一元一次方程和不等式出发，将同样表达式 kx+b(=0 和＜0)与 y=kx+b 进行非常，要求 学 学生画出变量 y=kx+b 的图像，引导学生观察图像中各个别点（被 X 轴分成的三部份）的纵坐标表示的地理 策 意义（y＞0，＝0，＜0），将图形与它的代数表示方式真正确立联系，并用语言分别概括起来，达到突破难 略 点。其过程以学生“自主研究”为主，教师鼓励为辅，设计的弊端从易到难，从简单到复杂，层层推进， 分 让学生在观察、分析，比较和交流合作中产生自己对物理常识的理解跟有效的学习方式。 析 3．设计了两组练习题。让学员通过自我解答、不同方法的对比来渗透识图能力的培育和数形结合的观念。

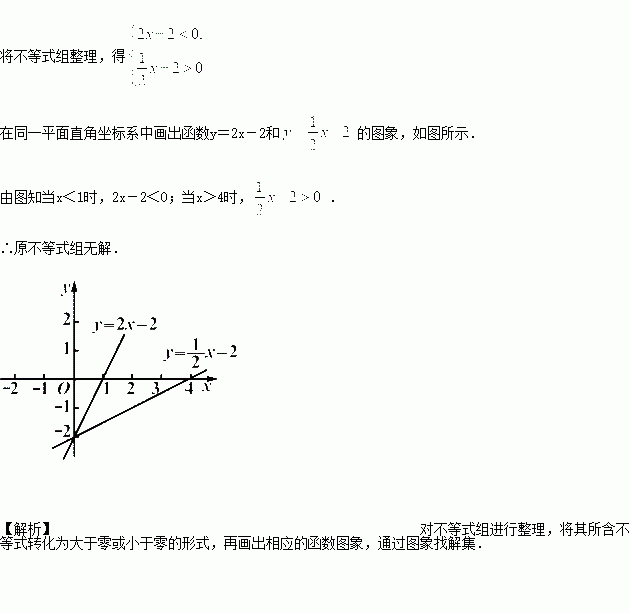
4．习题由易而难，在巩固的基础上有所提高，必做题和选做题的设定也使“不同的人在数学上受到不同的 发展”。 教 具 安 学生教学自主研究材料、多媒体课件。 排 课 时 这节内容安排两个课时，本节课是第一课时，主要借助研究活动领悟一次函数与一元一次方程、一次不 安 等式之间的联系。 排 问题与情景 教学过程设计 师生活动 设计意图 复 小明的老爸应邀来到上海投资， 师：从高中到目前我们学过 贴切的生活情景可以使大多数同 习 在庐阳工业园投资 300 万元成本建立 哪些解决难题的方式？ 学想到解决难题的方式，除了可促使学 旧 知、 学 前 一个小型家电制造厂家。建成交付后, 不考量材料费等其它原因，每年利润 75 万元。回答以下两个问题， 生：小学的算术法跟高中学 过的等式、不等式。 师：怎样运用函数图像解决 生的求知欲，也使教师初步感受一次方 程和一元一次不等式与一次函数是有 联系的，引入课题。 热 1:该厂家投产几年刚好收回成本？ 上面的难题呢？ 身 2:该工厂从那一年后盈利开始达到 300 万元以上? 活动一：探究一次函数与一元一次方 程之间的联系。

1．解方程 3x+6=0。 学生口答三个问题。 引题分解难度，给学生提供了反思 2．直线 y=3x+6 与 x 轴交点的坐标是 的视角和方向。 什么？ 3．讨论:图象与方程的解之间的关系。 合 作 交 流、 探 师：课前使你们打算了任意 通过师生反复实践和学生鼓励，学 的一次函数的图像，观察你 生从“形”到“数”，或者从“数”到 的图象，在图象中还有类似 “形”，自己研究一次函数的图像与一 的联系吗？ 元一次方程解的关系，体验知识生成的 学生举例说明。 过程。 究 师：将刚刚的探讨概括为一 新 般形式呢？ 知 归纳：一次函数 y=kx+b（k、 b 为系数，k≠0）与 x 轴交 4.不解方程：你可写出方程 3x+6=6 的 点的横坐标就是方程 kx+b=0 解吗？ 的解。 一元一次方程 kx+b=0（k、b 为系数，k≠0）的解就是一 次函数 y=kx+b(k ? 0 )与 x 轴 交点的横坐标。 5．合作交流（一） 你能够运用图像 师：请写出几个这样的一元 增