【综述】分数阶傅里叶变换(FRFT)

作者：WTT整理

傅里叶级数（傅里叶变换）几乎在所有科学和工程领域发挥着重要作用。黎曼积分和勒贝格积分均起源于对傅里叶级数的研究，傅里叶级数（傅里叶变换）在齿轮箱故障诊断分析上也有广泛应用，是目前齿轮箱技术研究的热点之一，特别是分数阶傅里叶变换（FRFT，fractional Fourier transform），在齿轮箱早期故障的诊断上，具有良好的发展潜力。

1. 历史回顾

三角函数展开起源于18世纪。1808年，傅里叶在他著名的热力学论文集“热的分析理论”中详细的研究了三角级数，并用三角级数成功的解决了许多热传导问题的偏微分方程。由于当时傅里叶的结论并无确凿证据及数学家对傅里叶的观点还很陌生，所以傅里叶的研究当时饱受争议，并且人们还认为他夸大了结论的适用范围。事实上，目前数学家已经证明了傅里叶级数足以表示绝大多数曲线。

将傅里叶级数的定义域拓展到整个实轴上，就得到了傅里叶变换。傅里叶变换是分析和处理平稳信号的一种标准和有力的工具，但随着研究范围的扩大逐渐也显示出了它的局限性：主要是傅里叶变换是全局变换，得到的是信号的整体频谱，因而无法表述时频的局部特征，因此人们进一步提出了分数阶傅里叶变换，短时傅里叶变换。

分数阶傅里叶变换最早是纳米亚（Namias）于1980年提出，其目的是用于求解量子力学中出现的线性时变偏微分方程。随后麦克布莱德（McBride）等对FRFT理论从数学上以积分形式给出了严格定义。1993年洛曼（Lohmann）阐述了FRFT的物理意义，即可理解为时频平面的旋转，洛曼（Lohmann）开创性的工作使得FRFT首先在光学中得到应用。

FRFT实际上是一种统一的时频变换，同时反映了信号在时域和频域上的信息，与传统的傅里叶变换相比，它适用于处理非平稳信号，尤其是线性调频信号，这使得FRFT在齿轮箱故障诊断上也得到越来越多的应用。

以下我们通过定义来了解它们之间的关系。

2. 傅里叶级数定义：

傅里叶级数就是将某一函数改写成正弦（sin）函数和余弦（cos）函数的和的形式。

2.1 傅里叶级数在[-π,л]区间上的形式为：

2.2 傅里叶级数拓展到任意周期区间[-a,a]上的形式为：

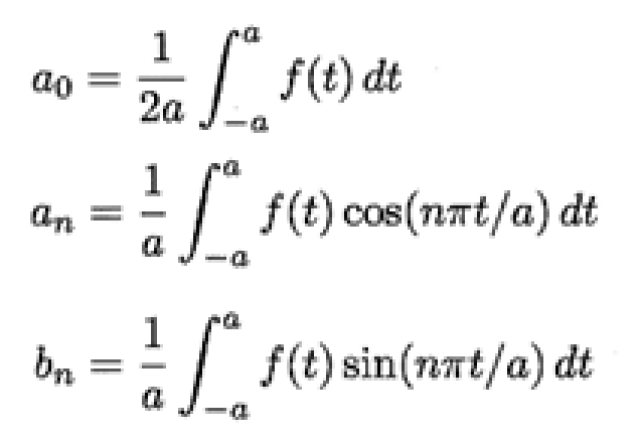
2.3 将以上形式改写成复数形式为

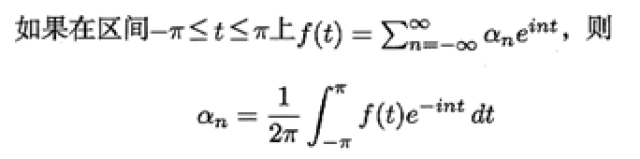
如果我们将[-a.a]区间拓展到整个实轴上阶越函数的傅立叶变换，就引出以下傅里叶变换定义。

3. 傅里叶变换定义：

我们用F表示傅里叶算子，如果对信号f（t）连续进行傅里叶变换，则有:

FF[f(t)]=F2[f(t)]=f(-t)；

F3[f(t)]=f(-λ)；

F4[f(t)]=f(t)；

如果我们将t轴（时间轴）与λ（频率轴）轴构成一个直角坐标系，将每次的傅里叶变换看作坐标轴的90度旋转阶越函数的傅立叶变换，在每次旋转的同时改变f（t）的表达形式，则这种坐标系定义的t-λ平面（可理解为时间-频率平面）满足以上傅里叶变换的性质。

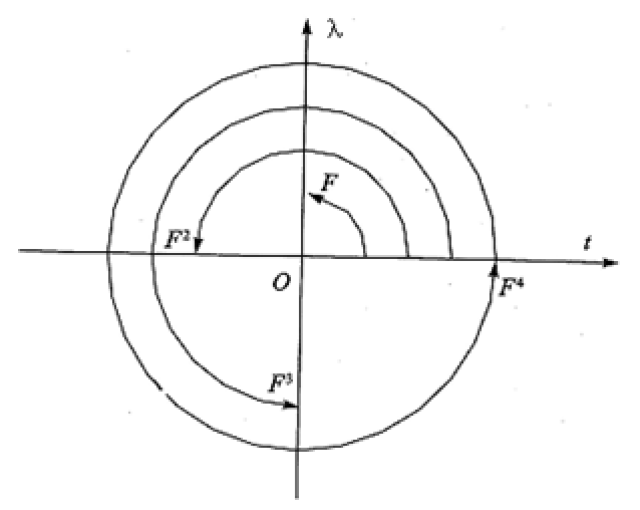
图1傅里叶变换t-λ平面（时-频平面）表示

显然，时频平面的90度旋转对应一次傅里叶变换，那么时频平面的任意角度α旋转的数学定义和物理意义是什么呢?这就引出了以下的分数阶傅里叶变换的定义。

4. 分数阶傅里叶变换定义：

j为复数符号，p为傅里叶阶数。当p=1时，f1（u）就是f（t）的普通的傅里叶变换；当p=-1时，f-1（u）就是f（t）的普通的傅里叶逆变换；同时，FRFT满足阶数可加性（指数可加性，或旋转可加性），即FP1FP2=FP1+P2。所以可以认为分数阶傅里叶变换是一种广义的傅里叶变换。

5. 矩形波的FRFT展开:

通过下面矩形波不同阶次的展开图，能形象的理解信号从时域逐渐过渡到频域的过程。

f（t）=1，-4≤t＜4；f（t）=0，t是其它值时。

以下图2到图6中，实线表示FRFT的实部，虚线表示FRFT的虚部。当p很小时，FRFT的实部非常接近时域的矩形方波(见图2)；当p值接近于1时，FRFT的结果就接近矩形波的傅里叶变换，即sinc函数（见图6）。

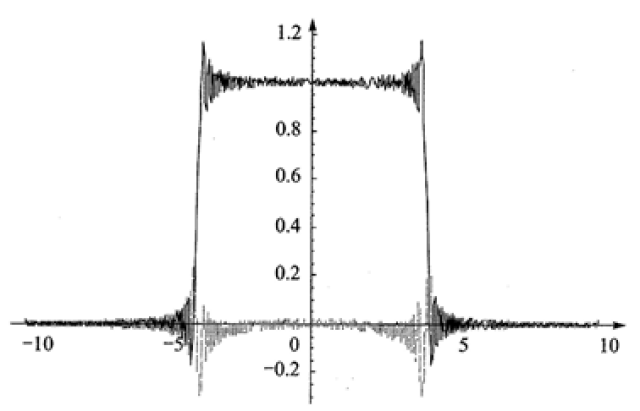
图2 p=0.005时的FRFT

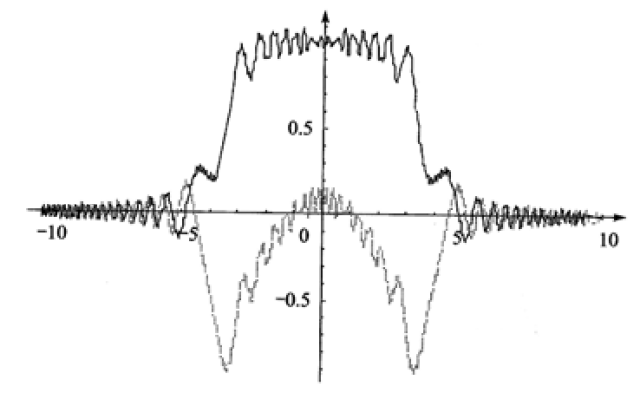
图3 p=0.1时的FRFT

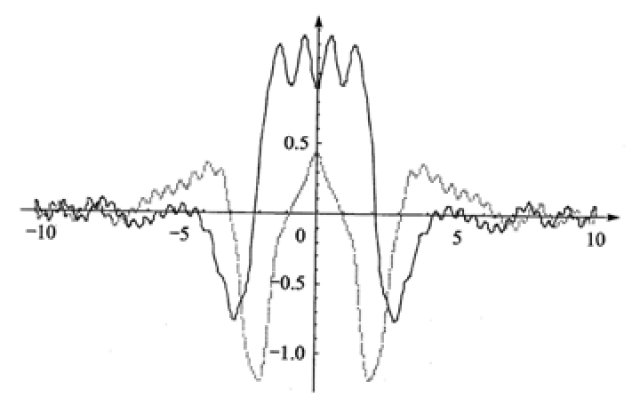
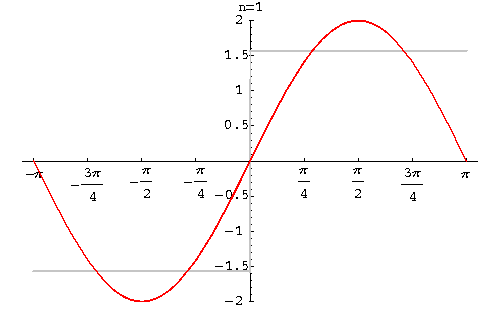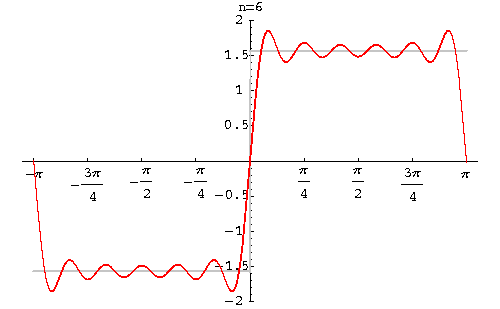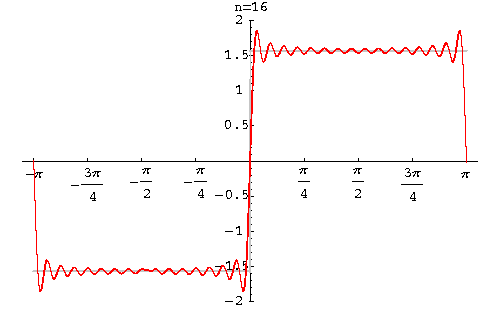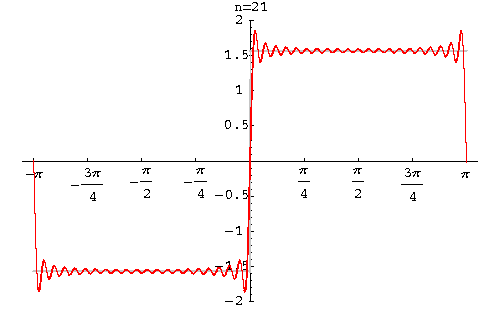
图4 p=0.4时的FRFT

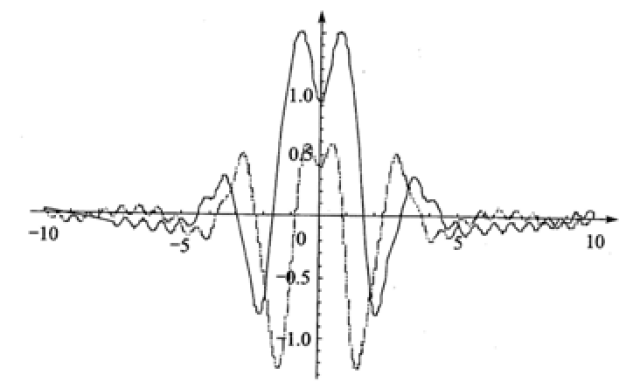
图5 p=0.6时的FRFT

图6 p=0.995时的FRFT

参考文献：

E-mail：

Suzhou Walnut Transmission Technology Co.，ltd

Perfect Design Comes From Profession And Experience

声明：该文观点仅代表作者本人，搜狐号系信息发布平台，搜狐仅提供信息存储空间服务。