matlab快速傅里叶变换（三个matlab程序介绍）

（十六） 傅里叶级数 1、傅里叶级数：三角函数系的正交性。14. 会将定义在闭区间[-l, l)上的黎曼可积函数延拓成周期为2l的函数并展开其傅里叶级数, 会将定义在[0, l) 上的函数展开为正弦级数与余弦级数, 会写出傅里叶级数的和函数的表达式.。2 . 3 周期信号的傅利叶级数分析 1. 三角形式的傅利叶级数 令 f t 为周期信 号, 周期为 t , 且满足狄里赫利条件 * 一般 实际信 号均满足 , 则f t 可展开为 以下级数 : ∞ f t a0 + ∑ an cos nω0 t + bn sin nω0 t 2 .3 .1 n 1 c + t 1式中: a0 ∫ f t d t t c c + t 2 an ∫ f t cos n ω0 td t t c c + t 2 b f t sin n ω td t n ∫ 0 t c t其中: c 为常数 , 其值可任选 。

傅里叶变换在物理学、电子类学科、数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学、海洋学、结构动力学等领域都有着广泛的应用（例如在信号处理中，傅里叶变换的典型用途是将信号分解成幅值谱——显示与频率对应的幅值大小）。

傅里叶变换（fft）matlab程序一

Fs = 128; % 采样频率

T = 1/Fs; % 采样时间

L = 256; % 信号长度

t = （0:L-1）*T; % 时间

x = 5 + 7*cos（2*pi*15*t - 30*pi/180） + 3*cos（2*pi*40*t - 90*pi/180）; %cos为底原始信号

y = x + randn（size（t））; %添加噪声 figure; plot（t，y）

title（‘加噪声的信号’）

xlabel（‘时间（s）’）

N = 2^nextpow2（L）; %采样点数，采样点数越大，分辨的频率越精确，N》=L，超出的部分信号补为0

Y = fft（y，N）/N*2; %除以N乘以2才是真实幅值，N越大，幅值精度越高

f = Fs/N*（0:1：N-1）; %频率

A = abs（Y）; %幅值

P = angle（Y）; %相值

figure;

subplot（211）;plot（f（1:N/2），A（1:N/2））; %函数fft返回值的数据结构具有对称性，因此我们只取前一半

title（‘幅值频谱’）;

xlabel（‘频率（Hz）’）;

ylabel（‘幅值’）;

subplot（212）;

plot（f（1:N/2），P（1:N/2））;

title（‘相位谱频’）;

xlabel（‘频率（Hz）’）;

ylabel（‘相位’）;

傅里叶变换（fft）matlab程序二

tp=0:2048; % 时域数据点数

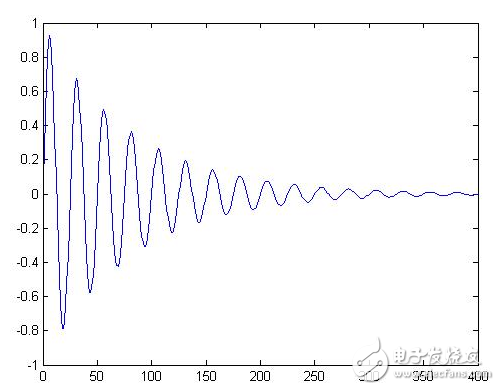
N yt=sin（0.08*pi*tp）.*exp（-tp/80）; % 生成正弦衰减函数

plot（tp，yt）， axis（［0，400，-1，1］）， % 绘正弦衰减曲线

t=0:800/2048:800; % 频域点数Nf

f=0:1.25:1000;

yf=fft（yt）; % 快速傅立叶变换

ya=abs（yf（1:801））; % 幅值

yp=angle（yf（1:801））*180/pi; % 相位 y

r=real（yf（1:801））; % 实部

yi=imag（yf（1:801））; % 虚部

figure subplot（2，2，1）

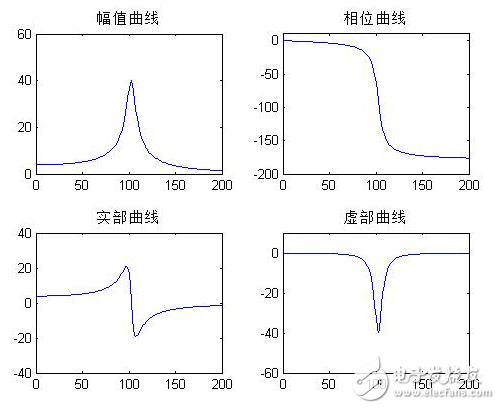
plot（f，ya），axis（［0，200，0，60］） % 绘制幅值曲线

title（‘幅值曲线’）

subplot（2，2，2）

plot（f，yp），axis（［0，200，-200，10］） % 绘制相位曲线

title（‘相位曲线’）

subplot（2，2，3）

plot（f，yr），axis（［0，200，-40，40］） % 绘制实部曲线

title（‘实部曲线’）

subplot（2，2，4）

plot（f，yi）阶越函数的傅立叶变换，axis（［0，200，-60，10］） % 绘制虚部曲线

title（‘虚部曲线’）

结果

傅里叶变换（fft）matlab程序三

clear all %清除内存所有变量

close all %关闭所有打开的图形窗口

%% 执行FFT点数与原信号长度相等（100点）

% 构建原信号

N=100; % 信号长度（变量@@@@@@@）

Fs=1; % 采样频率

dt=1/Fs; % 采样间隔

t=［0:N-1］*dt; % 时间序列

xn=cos（2*pi*0.24*［0:99］）+cos（2*pi*0.26*［0:99］）;

xn=［xn，zeros（1，N-100）］; % 原始信号的值序列

subplot（3，2，1） % 变量@@@@@@@

plot（t，xn） % 绘出原始信号

xlabel（‘时间/s’），title（‘原始信号（向量长度为100）’） % 变量@@@@@@@

% FFT分析

NN=N; % 执行100点FFT

XN=fft（xn，NN）/NN; % 共轭复数，具有对称性

f0=1/（dt*NN）; % 基频

f=［0:ceil（（NN-1）/2）］*f0; % 频率序列

A=abs（XN）; % 幅值序列

subplot（3，2，2），stem（f，2*A（1:ceil（（NN-1）/2）+1）），xlabel（‘频率/Hz’） % 绘制频谱（变量@@@@@@@）

axis（［0 0.5 0 1.2］） % 调整坐标范围

title（‘执行点数等于信号长度（单边谱100执行点）’）; % 变量@@@@@@@

%% 执行FFT点数大于原信号长度

% 构建原信号

N=100; % 信号长度（变量@@@@@@@）

Fs=1; % 采样频率

dt=1/Fs; % 采样间隔

t=［0:N-1］*dt; % 时间序列

xn=cos（2*pi*0.24*［0:99］）+cos（2*pi*0.26*［0:99］）;

xn=［xn，zeros（1，N-100）］; % 原始信号的值序列

subplot（3，2，3） % 变量@@@@@@@

plot（t，xn） % 绘出原始信号

xlabel（‘时间/s’），title（‘原始信号（向量长度为100）’） % 变量@@@@@@@

% FFT分析

NN=120; % 执行120点FFT（变量@@@@@@@）

XN=fft（xn，NN）/NN; % 共轭复数，具有对称性

f0=1/（dt*NN）; % 基频

f=［0:ceil（（NN-1）/2）］*f0; % 频率序列

A=abs（XN）; % 幅值序列

频域中其二维傅立叶频谱除了直流成分所对应的峰外， 还存在两个对称的频谱峰，刻画了局部纹线的方向和频率：纹线频率对应于两 个频谱峰之间的距离，其方向与两峰连线的方向垂直【４习。会议期间，联合国外空司还组织有关专家开展了“gnss频谱保护和干扰检测与减轻”“空间天气及对gnss的影响”两个专题的研讨，内容涉及卫星导航原理、gnss信号特点和干扰分析、itu介绍、无线电频谱管理、gnss干扰欺骗事件和各国目前出台的政策措施等，旨在倡导各国重视卫星导航频率保护，为gnss应用提供一个安全可靠的频率环境。 * 2、绘制圆弧(主要分为：绘制填充圆弧和绘制圆弧边框利用isfill变量来标记,注意：在绘制圆弧边框的时候还有一种特殊情况就是，只需要仅仅绘制弧边，不需要绘制圆弧开始起点和终点之间的连线，这个就是调用了beginpath()不需要调用closepath(),这里也使用一个isonlyarc变量来标记true为仅仅绘制弧边。

axis（［0 0.5 0 1.2］） % 调整坐标范围

title（‘执行点数大于信号长度（单边谱120执行点）’）; % 变量@@@@@@@

%% 执行FFT点数与原信号长度相等（120点）

% 构建原信号

N=120; % 信号长度（变量@@@@@@@）

Fs=1; % 采样频率

dt=1/Fs; % 采样间隔

t=［0:N-1］*dt; % 时间序列

xn=cos（2*pi*0.24*［0:99］）+cos（2*pi*0.26*［0:99］）;

xn=［xn，zeros（1，N-100）］; % 原始信号的值序列

subplot（3，2，5） % 变量@@@@@@@

plot（t，xn） % 绘出原始信号

xlabel（‘时间/s’），title（‘原始信号（向量长度为120）’） % 变量@@@@@@@

% FFT分析

NN=120; % 执行120点FFT（变量@@@@@@@）

XN=fft（xn，NN）/NN; % 共轭复数阶越函数的傅立叶变换，具有对称性

f0=1/（dt*NN）; % 基频

f=［0:ceil（（NN-1）/2）］*f0; % 频率序列

A=abs（XN）; % 幅值序列

subplot（3，2，6），stem（f，2*A（1:ceil（（NN-1）/2）+1）），xlabel（‘频率/Hz’） % 绘制频谱（变量@@@@@@@）

axis（［0 0.5 0 1.2］） % 调整坐标范围

title（‘执行点数等于信号长度（单边谱120执行点）’）; % 变量@@@@@@@

结果