对数函数教案下载 【教学设计】河北定州实验中学杨丽先(一)
(完整版)对数函数教学设计_数学_高中教育_教育专区

21人阅读|1次下载

(完整版)对数函数教学设计_数学_高中教育_教育专区。对数函数》教学设计 河北定州实验中学 杨丽先 一、教材分析 本节课是新课标高中数学必修①中第三章对数函数内容的第二课时, 也就 是对数 函数的入门 . 对数函数对于学生来说是一个全新的变量建模, 学习

对数函数》教学设计 河北定州实验中学 杨丽先 一、教材分析 本节课是新课标高中数学必修①中第三章对数函数内容的第二课时, 也就 是对数 函数的入门 . 对数函数对于学生来说是一个全新的变量建模, 学习出来非常困难 . 而对数函数又是本章的重要内容, 在高考中占有一定的分量, 它是在指数函数的 基础 上,对函数类别的拓广, 同时在缓解一些日常生活问题及科研中起非常重要 的作用. 通过 本节课的学习,可以使学生理解对数函的概念,从而进一步加强对 对数模型的了解与理 解。同时,通过对数概念的学习,对培养教师对立统一,相 互联系、相互转化的观念,培 养学生的逻辑思维能力都具备重要的含义 . 二、学情分析 大部分学生学习的自主性较差, 主动性不够,学习有依赖性, 且学习的自信不足, 对数 学存在或多或少的恐惧感 . 通过对指数函与指数函数的学习,学生已多次体 会了对立统 一、相互联系、相互转换的观念,并且研究素养、逻辑思维能力受到 了一定的锻炼 . 因 此,学生未具有了构建发现研究对数函数定义的了解基础,故 应借助指导,教会学生独立 思考、大胆探索和灵活采用类比、转化、归纳等物理 思想的学习方法 . 三、设计模式 学生是课堂的主体 , 本节课要帮学员提供各类参与机会 . 为了激发学生学习 的积 极性,使学生化被动为主动 .本节课我利用多媒体辅助教学 , 教学中我鼓励教师从 实 例出发,从中认识对数的建模,体会引入对数的必要性 . 在教学重难点上对数函数教案下载,步 步设问、启 发学生的认知 ,通过教学训练、探究活动 ,学生探讨的方法来增进理解 , 很好地突破瓶颈和 提高教学效益 . 让学员在学生的鼓励下,充分地动手、动口、 动脑,掌握学习的主动权 . 四、教学目标 1、理解对数函数的概念 , 了解对数函数与指数函数的关系; 理解对数函数的性质, 掌握 以上知识并产生技能 . 2、通过对数函数的学习,树立相互联系,相互转换的见解,渗透数形结合,分 类探讨的 思想. . 3、通过学生分组研究进行活动,掌握对数函数的重要性质。

通过做练习,使学 生感受到 理论与实践的统一 . 4、培养学生的类比、分析、归纳能力,严谨的认知品质并且在学习过程中培养 学生研究 的观念 . 五、重点与难点 重点 :( 1)对数函数的概念;( 2)对数函数与指数函数的相互转化 . 难点 :( 1)对数函数概念的理解;( 2)对数函数性质的理解 . 六、过程设计 (一) 复习导入 (1)复习提问:什么是对数函数?如何求反函数?指数函数的图像和性质如何? 学生回 答,并用课件展示 指数函数的图像跟性质。 设计动机: 设计的回答既与本节内容有紧密关系, 又有利于引入新课, 为教师理 解新 知识清除了障碍,有意识地培养学生探讨问题的素养。 (2)导言:指数方程有没有反函数?如果有,如何求指数函数的反函数?它的 反函数是 什么? 设计动机:这样的后记可促使学生求知欲,使学生渴求知道问题的答案。 (二) 讲授新课 (1)对数函数的概念 引导学生从对数式与指数式的关系及反函数的概念进行探讨并计算 出, 指数 函数有反函数,并且 y=ax(a>0 且 a≠1)的反函数是 y=logax,见课件。把 函数 y=logax 叫做对数函数,其中 a>0 且 a≠1。
从而引发对数函数的概念,展示课件。 设计动机: 对数函数的概念非常抽象对数函数教案下载, 利用尚未学过的常识逐步分析, 这样引出 对数 函数的概念过渡自然,学生容易接受。因为对数函数是指数函数的反函数 让学生非常它们 的定义域、值域、对应法则及图像的关系,培养学员参加意识, 通过非常充分展现指数函 数及对数函数的内在联系。 (2)对数函数的图像 提问:同指数函数一样,在学习了函数的定义后来,我们要画函数 的图像,应如 何画对数函数的图像呢 让学生探讨并提问, 用描点法作图。 教师肯定, 我们每学习一种新的函数都可以 根据 函数的解析式, 描点画图。再考虑一下, 我们还可以用哪个方法画出对数函 数的图象 呢? 让学生提问,画出指数函数关于直线 y=x 对称的图像,就是对数函数的图象。 教师总 结:我们画对数函数的图像,既可用描点法,也只用图象变换法,下边我 们运用两种方式 画对数函数的图像。 方法一(描点法)首先列举 x,y(y=log2x,y=log x )值的对应表,因为对数函数 的定义 域为 x>0,因此可取 x=··· , , ,1,2,4,8···,请计算对应的 y 然后在坐标系内描点、画 出他们的图像 . 方法二(图象变换法)因为对数函数和指数函数互为反函数 , 图象关于直 线 y=x 对称,所以即使画出 y=ax 的图像关于直线 y=x 对称的曲线,就可以得到 y=logax. 的图象。
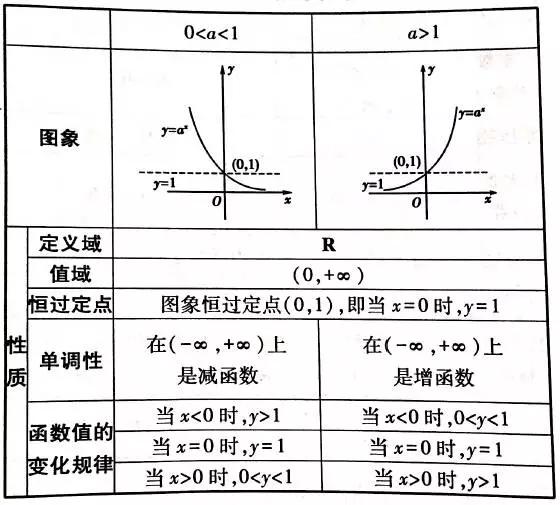
学生动手做实验,先描出 y=2x 的图像,画出它关于直线 y=x 对称的曲 线,它就是 y=log2x 的图像;类似的从 y=( )x 的图像画出 y=log x 的图像 ,再演 示课 件 ,教师加以解释。 设计动机: 用这些对称变换的方式画函数的图像, 可以增进和巩固学生对互为反 函数的 两个函数之间的了解, 便于将对数函数的图像和性质与指数函数的图像跟 性质对照, 但 使用描点法画函数图像更为方便, 两种方式能同时进行, 分析画法 之后,可使学生自由 选择画法。这样可以充分激发学生自主学习的积极性。 (3)对数函数的性质 在理解对数函数定义的基础上,掌握对数函数的图像跟性质是本节 的重点, 关键在于把握对数函数是指数函数的反函数这一要点, 讲对数函数的性质, 可 先 在同一坐标系内画出上述两个对数函数的图像, 根据图象让学生列表分析他们的 图象 特征跟性质,然后出示课件,教师补充。作了以上预测以后,再分 a>1 与 0