总结知识：高一语文选修1《对数函数》教案

教案是学生为成功而有效地举办课堂活动，根据教学大纲 和教科书要求及学生的实际状况，以课时或课题为单位，对教学内容、教学方法、教学方法等进行的详细设计跟安排的一种实用性教学文书。面是学习啦小编为你们整理的高二英语选修1《对数函数》教案，希望对你们有所帮助!

高一数学必修1《对数函数》教案

教学目标：

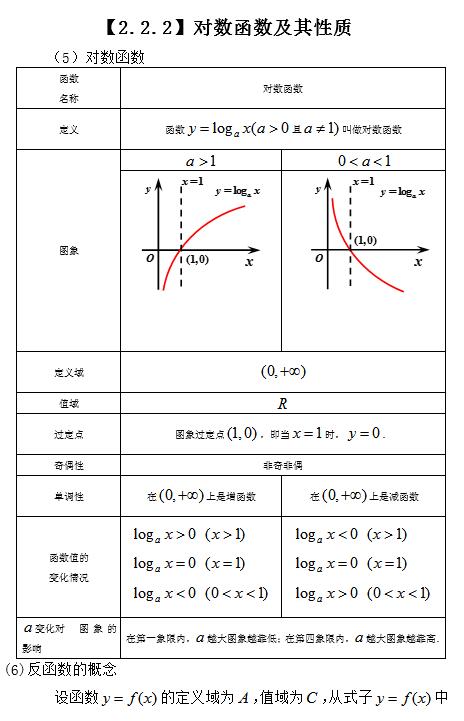
①掌握对数函数的性质。

②应用对数函数的性质可以缓解：对数的大小比较，求复合函数的定义域、值 域及单调性。

③ 注重函数思想、等价转换、分类争论等观念的渗透,提高

解题能力。

教学重点与难点：对数函数的性质的应用。

教学过程设计：

⒈复习提问：对数函数的概念及性质。

⒉开始正课

1 比较数的大小

例 1 比较下列各组数的大小。

⑴loga5.1 ,loga5.9 (a>0,a≠1)

⑵log0.50.6 ,logЛ0.5 ,lnЛ

师：请同学们观察一下⑴中这两个对数有何特征?

生：这两个对数底相同。

师：那么针对两个底相同的对数如何比大小?

生：可构造一个以a为底的对数函数，用对数函数的单调性比大小。

师：对，请叙述一下这道题的解题过程。

生：对数函数的单调性取决于底的大小：当0

调递减，所以loga5.1>loga5.9 ;当a>1时，函数y=logax单调递

增，所以loga5.1

板书：

解：Ⅰ)当0

∵5.1loga5.9

Ⅱ)当a>1时，函数y=logax在(0，+∞)上是增函数，

∵5.1

师：请同学们观察一下⑵中这三个对数有何特征?

生：这三个对数底、真数都不相等。

师：那么针对这三个对数如何比大小?

生：找“中间量”， log0.50.6>0，lnЛ>0，logЛ0.51，

log0.50.6

板书：略。

师：比较对数值的大小常见方式：①构造对数函数，直接利用对数函

数 的单调性比大小，②借用“中间量”间接比大小，③利用对数

函数图像的位置关系来比大小。

2 函数的定义域, 值 域及单调性。

例 2 ⑴求方程y=的定义域。

⑵解不等式log0.2(x2+2x-3)>log0.2(3x+3)

师：如何来求⑴中方程的定义域?(提示：求函数的定义域，就是要

使函数有含义。若变量中带有分母，分母不为零;有偶次根式，

被开方法大于或等于零;若变量中有对数的方式，则真数大于

零，如果函数中同时发生以上几种情况，就要全部考虑进去，求

它们共同作用的结果。)

生：分母2x-1≠0且偶次根式的被开方法log0.8x-1≥0，且真数x>0。

板书：

解：∵ 2x-1≠0 x≠0.5

log0.8x-1≥0对数函数教案下载， x≤0.8

x>0 x>0

∴x(0,0.5)∪(0.5,0.8〕

师：接下来我们一起来解这个不等式。

分析：要解这个不等式,首先应让这个不等式有含义，即真数大于零，

再依据对数函数的单调性求解。

师：请你写一下这道题的解题过程。

生：

解： x2+2x-3>0

x1

(3x+3)>0, x>-1

x2+2x-30,a≠1)

师：求例3中方程的的斜率和单调区间应用及复合函数的观念方法。

下面请同学们来解⑴。

生：此函数能看作是由y= log0.5u, u= x- x2复合而成。

板书：

解：⑴∵u= x- x2>0, ∴0

u= x- x2=-(x-0.5)2+0.25, ∴0

∴y= log0.5u≥log0.50.25=2

∴y≥2

x x(0,0.5] x[0.5,1)

u= x- x2

y= log0.5u

y=log0.5(x- x2)

函数y=log0.5(x- x2)的单调递减区间(0,0.5]，单调递 增区间[0.5,1)

注：研究任何变量的性质时，都必须首先确保这个函数有意义，否则

函数都不存在，性质就无从谈起。

师：在⑴的基础上，我们一起来解⑵。请同学们观察一下⑴与⑵有什

生：⑴的底数是常值，⑵的底数是字母。

师：那么⑵如何来解?

生：只要对a进行分类讨论，做法与⑴类似。

板书：略。

⒊小结

这堂课主要讲解怎样应用对数函数的性质解决一些难题，希望可

通过这堂课使同学们对等价转换、分类争论等观念加以应用，提高解题能力。

⒋作业

⑴解不等式

①lg(x2-3x-4)≥lg(2x+10);②loga(x2-x)≥loga(x+1),(a为常数)

⑵已知变量y=loga(x2-2x)，(a>0,a≠1)

①求它的单调区间;②当0

⑶已知变量y=loga (a>0, b>0, 且 a≠1)

①求它的定义域;②讨论它的奇偶性; ③讨论它的单调性。

⑷已知变量y=loga(ax-1) (a>0,a≠1),

①求它的定义域;②当x为何值时，函数值大于1;③讨论它的

单调性。

5.课堂教学设计说明

这节课是安排为习题课，主要运用对数函数的性质解决一些难题对数函数教案下载，整个一堂课分两个部分：一 .比较数的大小,想借助这一部分的练习，

培养同学们构造函数的观念跟分类争论、数形结合的观念。二.函数的定义域, 值 域及单调性，想借助这一部分的训练，能使同学们重视求方程的定义域。因为学生在求方程的导数和单调区间时，往往不考量函数的定义域，并且这些错误更顽固，不易纠正。因此，力求学生做到想法正确，步骤清晰。为了激发学生的积极性，突出学生是教学的主体，便把例题分了层次，由易到难，力求做到每题都可由学生独立完成。但是，每一道题的审题过程，老师都必须给与板书，这样又使教师有了获得新知识的幸福，又不必为了解题格式的不熟悉而烦恼。每一题讲完后，由学生简明扼要地总结，以让好学生把握地更完善，较差的学生也无法跟上。

看过" 高一语文选修1《对数函数》教案 "的还看了:

1.高一语文对数函数教案

2.高一数学数列教案

3.高一数学必修一函数的基本性质教案