等腰三角形知识点及典型习题教案模板3( 【教学教研师训】等腰三角形(一)教学目标)

等腰三角形(一)
教学目标
1.等腰三角形的概念。 2.等腰三角形的性质。 3.等腰三角形的概念和性质的应用。
教学要点: 1.等腰三角形的概念和性质。 2.等腰三角形性质的应用。
教学难点:三线等腰三角形合一性质的理解与应用。
教学过程
我。提出问题,创造情境
在之前的学习中,我们学习了轴对称图形,探索了轴对称的性质,能够相对于线对称图形制作一个简单的平面图形,并且我们能够通过轴对称变换图案设计出一些漂亮的形状在本课中等腰三角形知识点及典型习题教案模板3,我们将从轴对称的角度认识一些熟悉的几何图形。我们来学习:①三角形是轴对称图形吗? ②什么样的三角形是轴对称图形?
有些三角形是轴对称图形,有些不是。
问题:什么样的三角形是轴对称图形?
满足轴对称条件的三角形为轴对称图形,即三角形沿某条直线对折后,两部分能完全重合为轴对称图形。
在本课中,我们将认识一种轴对称三角形──等腰三角形。
Ⅱ.介绍新课:让学生通过自己的思考制作一个等腰三角形。
做一条直线L,在L上取A点,在L外取B点,B点相对于直线L作对称点C,连接AB、BC、CA,得到一个等腰三角形。
等腰三角形的定义:两条边相等的三角形叫做等腰三角形。两条相等的边叫腰,另一边叫底,两腰之间的夹角叫顶角等腰三角形知识点及典型习题教案模板3,底与腰的夹角叫底角。在学生制作的等腰三角形中,标出腰部、底角、顶角和底角。
思考:
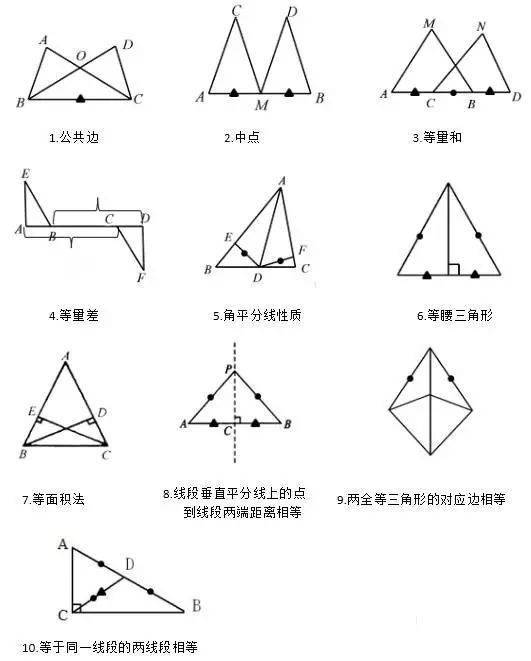
1.等腰三角形是轴对称图形吗?请找出它的对称轴。
2.等腰三角形的两个底角是什么关系?
3.顶点的平分线所在的直线是等腰三角形的对称轴吗?
4.中心线底边的线是等腰三角形的对称轴吗?底边高度所在的直线呢?
结论:等腰三角形是轴对称图形。它的对称轴是顶角平分线所在的直线。因为等腰三角形的两条腰是相等的,所以两条腰重叠,对折。
让学生折叠他们制作的等腰三角形,找出它的对称轴,看看它的两个底角之间的关系是什么。
沿等腰三角形顶角的平分线对折,发现两边部分重合。可以看出这个等腰三角形的两个底角相等,也可以知道顶角的平分线在底边。中线在底部边缘也很高。
由此,我们可以得到等腰三角形的性质:
1.等腰三角形的两个底角相等(简称“等边等角”)。
2.等腰三角形的顶角平分线、底边中线和底边高重合(通常称为“三线合一”)。
受上述折叠过程的启发,我们可以通过制作等腰三角形的对称轴得到两个全等三角形,并用三角形的全等来证明这些性质。学生们现在将亲手写出证明过程)。
如右图所示,在△ABC中,AB=AC,即底部BC的中线AD,因为
所以△BAD≌△CAD(SSS)。
所以∠B=∠C。
]如右图所示,在△ABC中,AB=AC,顶点∠BAC的角平分线AD,因为
所以△BAD≌△CAD。

所以BD=CD,∠BDA=∠CDA=∠BDC=90°。
【例1】如图,在△ABC中,AB=AC,D点在AC上,BD=BC=AD,
求:△ABC各角的度数。
分析:根据等边角和等边角的性质,我们可以得到
∠A=∠ABD, ∠ABC=∠C=∠BDC,
从∠BDC=∠A+∠ABD,我们可以得到∠ABC=∠C=∠BDC=2∠A。
从三角形内角和到180°,可以得到△ABC的三个内角。
如果将∠A设为x,那么∠ABC和∠C都可以用x表示,这使得过程更简单。
解:因为AB=AC,BD=BC=AD,
所以∠ABC=∠C=∠BDC。
∠A=∠ABD(等边等角)。
假设∠A=x,则∠BDC=∠A+∠ABD=2x,
因此∠ABC=∠C=∠BDC=2x。
所以在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180°,
求解 x=36°。在△ABC中,∠A=35°,∠ABC=∠C=72°。

【老师】接下来,我们将通过实践巩固本课所学的知识。
Ⅲ.课堂练习:1.课本P51练习1、2、3。 2.阅读课本P49~P51,然后总结。
四。课程总结
这一课我们主要讨论了等腰三角形的性质,并对这些性质进行了简单的应用。等腰三角形是一个轴对称图形,它的两个底角相等(等边角相等)。等腰三角形的对称轴是其顶角的平分线,顶角平分线都是底边的中线。 , 是底部的高度。
我们通过这门课学习,首先要理解和掌握这些属性,并能灵活运用。
Ⅴ.作业:课本P56练习12.3第1、2、3、4题。
黑板设计
12。 3.1.1 等腰三角形
一、设计方案做了一个等腰三角形
二、等腰三角形的性质:1.等边等边角2.三线合一
12。 3.1.1 等腰三角形(二)
教学目标
1、理解和掌握等腰三角形的判断定理和推论
2、 可以使用其属性来确定线段或角度的相等性。
教学重点:判断定理的应用及等腰三角形的推理
教学难点:正确区分等腰三角形的判断和性质,能用等腰三角形的判断定理证明线段相等。

教学过程:
一、复习等腰三角形的性质
二、新奖:
我提出问题并创造情境
显示幻灯片。为了估计一条从东向西流动的河流的宽度,选择了河流北岸(B点)的一棵树作为B标记,然后在树的南边(A点)画了一面小旗以南岸为标记)沿南边向东步行60°的距离到C时,测得的∠ACB为30°。这时,可以通过地质学家测量的AC长度来知道河流的宽度。
同学们想知道,这样估算河流宽度的依据是什么?带着这道题,引导学生学习“等腰三角形的判定”。
II 引入一个新类
1.研究内容取自性质定理的标题和结论的变化——在△ABC,∠B=∠C,那么AB=AC?
做一个有两个相等角的三角形,然后观察两个相等角的边的关系?
2.引导学生写出已知,并根据图进行验证。
2、Summary,经论证,此命题为真命题,即“等腰三角形定理”(黑板上的定理名称)。
强调,这个定理是三角形中角相等关系转化为边相等关系的重要依据。与性质定理类似,可称为“等角等边”。
4.引导学生在引文中讲解地质专家测量方法的依据。
III 示例题和练习
1.如图2
△ABC为等腰三角形的是[]

2. ① 如图3,已知△ABC中AB=AC。 ∠A=36°,那么∠C______(基于什么?)。
②如图4,已知在△ABC中,∠A=36°,∠C=72°,△ABC是一个______三角形(根据什么?)
③若已知∠A=36°,∠C=72°,BD将∠ABC交叉AC除以D,判断图5中腰三角形有______。
④若已知AD=4cm,则BC______cm。
3.以问题 l______ 的形式进行推论。
4.在问题形式 2______ 中得出推论。
示例:如果三角形外角的平分线与三角形的一边平行,请验证该三角形是等腰三角形。
分析:引导学生根据题意作图,写出已知,验证,分析证明。
练习:5. (l) 如图6所示,在△ABC,AB=AC中,∠ABC的平分线,∠ACB与F点相交,与F相交为DE//BC,与AB相交于D点,并在 E 处与 AC 相交。请问图中哪些三角形是等腰三角形?
(2)上题,如果去掉条件AB=AC,其他条件不变,图6中是否有等腰三角形?
练习:P53 练习1、2、3。
IV 类总结
1.判断三角形是否为等腰三角形的方法有几种?
2.判断三角形是否为等边三角形的方法有几种?
3.等腰三角形的性质定理和判断定理有什么关系?
4.现在要证明线段相等,一般要考虑多少方面?
V 分配作业:P56 页练习 12.3第5、6个问题
教案网123
奥巴马万岁