三角函数的求导公式是什么?

历史表明,重要数学概念对数学发展的作用是不可估量的,函数概念对数学发展的影响,可以说是贯穿古今、旷日持久、作用非凡,回顾函数概念的历史发展,看一看函数概念不断被精炼、深化、丰富的历史过程,是一件十分有益的事情,它不仅有助于我们提高对函数概念来龙去脉认识的清晰度,而且更能帮助我们领悟数学概念对数学发展,数学学习的巨大作用.
(一)
马克思曾经认为,函数概念来源于代数学中不定方程的研究.由于罗马时代的丢番图对不定方程已有相当研究,所以函数概念至少在那时已经萌芽.
自哥白尼的天文学革命以后,运动就成了文艺复兴时期科学家共同感兴趣的问题,人们在思索:既然地球不是宇宙中心,它本身又有自转和公转,那么下降的物体为什么不发生偏斜而还要垂直下落到地球上?行星运行的轨道是椭圆,原理是什么?还有,研究在地球表面上抛射物体的路线、射程和所能达到的高度,以及炮弹速度对于高度和射程的影响等问题,既是科学家的力图解决的问题,也是军事家要求解决的问题,函数概念就是从运动的研究中引申出的一个数学概念,这是函数概念的力学来源.
(二)
早在函数概念尚未明确提出以前,数学家已经接触并研究了不少具体的函数,比如对数函数、三角函数、双曲函数等等.1673年前后笛卡儿在他的解析几何中,已经注意到了一个变量对于另一个变量的依赖关系,但由于当时尚未意识到需要提炼一般的函数概念,因此直到17世纪后期牛顿、莱布尼兹建立微积分的时候,数学家还没有明确函数的一般意义.
1673年,莱布尼兹首次使用函数一词表示“幂”,后来他用该词表示曲线上点的横坐标、纵坐标、切线长等曲线上点的有关几何量.由此可以看出,函数一词最初的数学含义是相当广泛而较为模糊的,几乎与此同时,牛顿在微积分的讨论中,使用另一名词“流量”来表示变量间的关系,直到1689年,瑞士数学家约翰·贝努里才在莱布尼兹函数概念的基础上,对函数概念进行了明确定义,贝努里把变量x和常量按任何方式构成的量叫“x的函数”,表示为yx.
当时,由于连接变数与常数的运算主要是算术运算、三角运算、指数运算和对数运算,所以后来欧拉就索性把用这些运算连接变数x和常数c而成的式子,取名为解析函数,还将它分成了“代数函数”与“超越函数”.
用“a”来表示该词项所对应的概念的话,那么,对于任意一个对象来说,它总是或者属于“a”的外延,或者属于“非a”的外延。考试内容: (一) 常数项级数:收敛与发散的概念, 收敛级数的和的概念, 级数的基本性质与收敛的必要条件, 几何级数与, p 级数及其收敛性, 正项级数收敛性的判别法, 交错级数与莱布尼茨定理, 任意项级数的绝对收敛与条件收敛. (二) 函数项级数:收敛域、和函数、一致收敛概念, 函数项级数的一致收敛判别法、和函数的分析性质(连续性、可微性和可积性。在规定的频率范围内,振动台轴向以80%最大振动幅值作扫频振动,用记录仪分别记录台面振动方向频率函数曲线和另两个相互垂直并垂直于振动方向和垂直于耳轴轴线的两条频率曲线,从而确定最大横向运动比和对应的频带宽度。
(三)
11应用radians函数将角度转换为弧度18312应用sin函数计算给定角度的正弦值18413应用sinh函数计算某数字的双曲正弦值18514应用tan函数计算给定角度的正切值18515应用tanh函数计算某一数字的双曲正切1864综合实战:计算员工加班费187第7章信息函数1881信息函数概述1882is类函数1891应用isblank函数判断单元格是否为空白1902应用iserr或iserr。第二是算力,计算的成本在不断下降,服务器越来越强大,过去我们觉得人工智能不实用,是因为算力太大,但今天算力已经到了一个临界点,可以使得很多的人工智能应用变的实际,变得可用了。使用名称 803 在公式中使用区域名称 818综合实例:制作销售人员业绩核算表81第4章逻辑函数831判断真假值的逻辑函数831应用and函数进行交集运算842应用false函数判断逻辑值为假863应用not函数计算反函数874应用or函数进行并集运算885应用true函数判断逻辑值为真892进行复合检验的逻辑函数901应用if函数对真假函数进行判断902应用iferror函数自定义公式错误时的提。
后来,人们又给出了这样的定义:如果一个量依赖着另一个量,当后一量变化时前一量也随着变化,那么第一个量称为第二个量的函数.“这个定义虽然还没有道出函数的本质,但却把变化、运动注入到函数定义中去,是可喜的进步.”

在函数概念发展史上,法国数学家富里埃的工作影响最大,富里埃深刻地揭示了函数的本质,主张函数不必局限于解析表达式.1822年,他在名著《热的解析理论》中说,“通常,函数表示相接的一组值或纵坐标,它们中的每一个都是任意的……,我们不假定这些纵坐标服从一个共同的规律;他们以任何方式一个挨一个.”在该书中,他用一个三角级数和的形式表达了一个由不连续的“线”所给出的函数.更确切地说就是,任意一个以2π为周期函数,在〔-π,π〕区间内,可以由
表示出,其中
富里埃的研究,从根本上动摇了旧的关于函数概念的传统思想,在当时的数学界引起了很大的震动.原来,在解析式和曲线之间并不存在不可逾越的鸿沟,级数把解析式和曲线沟通了,那种视函数为解析式的观点终于成为揭示函数关系的巨大障碍.
通过一场争论,产生了罗巴切夫斯基和狄里克莱的函数定义.
1834年,俄国数学家罗巴切夫斯基提出函数的定义:“x的函数是这样的一个数,它对于每个x都有确定的值,并且随着x一起变化.函数值可以由解析式给出,也可以由一个条件给出,这个条件提供了一种寻求全部对应值的方法.函数的这种依赖关系可以存在,但仍然是未知的.”这个定义建立了变量与函数之间的对应关系,是对函数概念的一个重大发展,因为“对应”是函数概念的一种本质属性与核心部分.
1837年,德国数学家狄里克莱(Dirichlet)认为怎样去建立x与y之间的关系无关紧要,所以他的定义是:“如果对于x的每一值,y总有完全确定的值与之对应,则y是x的函数.”
根据这个定义,即使像如下表述的,它仍然被说成是函数(狄里克莱函数):
f(x)= 1(x为有理数),
0(x为无理数).
的增大, (1)如果函数在某个区间上随着自变量 的增大, )如果函数在某个区间上随着自变量x的增大 相应的f(x)也随着增大,我们就说函数在该区间上 也随着增大, 相应的 也随着增大 为增函数。 ( )f x 、( )g x 都不满足狄利克雷条件 11. 函数2xf x和函数1( )2xg x , 在[ 2,2]上在指定区间上( ) 。11.了解傅里叶级数的概念和狄利克雷收敛定理,会将定义在 上的函数展开为傅里叶级数,会将定义在 上的函数展开为正弦级数与余弦级数,会写出傅里叶级数的和函数的表达式.。
狄里克莱的函数定义,出色地避免了以往函数定义中所有的关于依赖关系的描述,以完全清晰的方式为所有数学家无条件地接受.至此,我们已可以说,函数概念、函数的本质定义已经形成,这就是人们常说的经典函数定义.
(四)

生产实践和科学实验的进一步发展,又引起函数概念新的尖锐矛盾,本世纪20年代,人类开始研究微观物理现象.1930年量子力学问世了,在量子力学中需要用到一种新的函数——δ-函数,
即ρ(x)= 0,x≠0,
∞,x=0.
且
δ-函数的出现,引起了人们的激烈争论.按照函数原来的定义,只允许数与数之间建立对应关系,而没有把“∞”作为数.另外,对于自变量只有一个点不为零的函数,其积分值却不等于零,这也是不可想象的.然而,δ-函数确实是实际模型的抽象.例如,当汽车、火车通过桥梁时,自然对桥梁产生压力.从理论上讲,车辆的轮子和桥面的接触点只有一个,设车辆对轨道、桥面的压力为一单位,这时在接触点x=0处的压强是
P(0)=压力/接触面=1/0=∞.
其余点x≠0处,因无压力,故无压强,即P(x)=0.另外,我们知道压强函数的积分等于压力,即
设s是一个非空集合,若r是关于s的有序元素对的一个关系,即对s中任意一个有序元素对(a,b),我们总能确定a与b是否满足条件r,就称r是s的一个关系(relation),又由于他是建立在二元(即s中任意两个元素)之上的,因此也称为二元关系。 该函数将集合init1中从first1到last1中的元素与集合init2中从first2到last2中的元素进行比较,将属于init1但不属于init2的元素形成一个序列,由x指示 (本例中将符合条件的元素用inserter函数插入到新的集合中)。默认的aggregate是sum,即结果集合中元素 的score是所有集合对应元素进行sum运算的值,而min和max是指,结果集合中元素的score是所有集合对应元素中最小值和最大值。
函数的现代定义与经典定义从形式上看虽然只相差几个字,但却是概念上的重大发展,是数学发展道路上的重大转折,近代的泛函分析可以作为这种转折的标志,它研究的是一般集合上的函数关系.
函数概念的定义经过二百多年来的锤炼、变革,形成了函数的现代定义,应该说已经相当完善了.不过数学的发展是无止境的,函数现代定义的形式并不意味着函数概念发展的历史终结,近二十年来,数学家们又把函数归结为一种更广泛的概念—“关系”.
设集合X、Y,我们定义X与Y的积集X×Y为
X×Y={(x,y)|x∈X,y∈Y}.
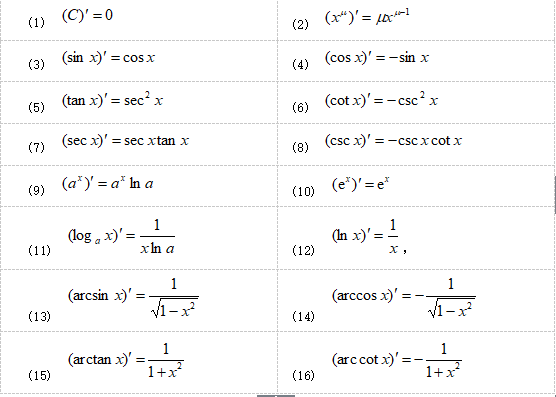
积集X×Y中的一子集R称为X与Y的一个关系,若(x,y)∈R,则称x与y有关系R,记为xRy.若(x,y)R,则称x与y无关系.
现设f是X与Y的关系,即fX×Y,如果(x,y),(x,z)∈f,必有y=z,那么称f为X到Y的函数.在此定义中,已在形式上回避了“对应”的术语,全部使用集合论的语言了.
体会函数是一种刻画变量之间关系的重要数学模型,体会对应关系在刻画函数概念中的作用。教材:人教a版高中数学必修4课题:2.1 平面向量的实际背景及基本概念授课教师:安徽省合肥市第一中学 刘娟一. 教学内容解析 向量是近代数学重要和基本的数学概念之一,它是沟通代数、几何与三角函数的桥梁,对更新和完善中学数学知识结构起着重要的作用. 向量集数与形于一身,有着极其丰富的实际背景,在现实生活中随处可见的位移、速度、力等既有大小, 又有方向的量是它的物理背景,有向线段是它的几何背景.向量就是从这些实际对象中抽象概括出来的数学概念,经过研究,建立起完整的知识体系之后,向量又作为数学模型,广泛地应用于解决数学、物理学科及实际生活中的问题,因此它在整个高中数学中起到联系数形、跨越学科、承前启后的作用.本课是“平面向量”的起始课,具有“统领全局”的作用. 本节概念课,更为重要的不是向量的形式化定义及几个相关概念,而是能让学生去体会认识与研究数学新对象的方法和基本思路,进而提高提出问题,分析问题,解决问题的能力.本节课主要内容包括向量的物理背景与概念,向量的表示,相等向量与共线向量.。函数概念的历史发展函数概念是中学中最重要的概念之一,它既是数学研究的对象,又是解决数学问题的基本思想方法。
三角函数是数学中属于初等函数中的超越函数的一类函数。它们的本质是任意角的集合与一个比值的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的,其定义域为整个实数域。另一种定义是在直角三角形中,但并不完全。现代数学把它们描述成无穷数列的极限和微分方程的解,将其定义扩展到复数系。
由于三角函数的周期性,它并不具有单值函数意义上的反函数三角函数求导公式推导。
三角函数在复数中有较为重要的应用三角函数求导公式推导。在物理学中,三角函数也是常用的工具。
基本初等内容
它有六种基本函数(初等基本表示):
函数名 正弦 余弦 正切 余切 正割 余割
(见:函数图形曲线)
三角函数图形曲线在平面直角坐标系xOy中,从点O引出一条射线OP,设旋转角为θ,设OP=r,P点的坐标为(x,y)有
正弦函数 sinθ=y/r

余弦函数 cosθ=x/r
正切函数 tanθ=y/x
余切函数 cotθ=x/y
正割函数 secθ=r/x
余割函数 cscθ=r/y
(斜边为r,对边为y,邻边为x。)
以及两个不常用,已趋于被淘汰的函数:
正矢函数 versinθ =1-cosθ
余矢函数 coversθ =1-sinθ
正弦(sin):角α的对边比上斜边
余弦(cos):角α的邻边比上斜边
正切(tan):角α的对边比上邻边
余切(cot):角α的邻边比上对边
正割(sec):角α的斜边比上邻边
余割(csc):角α的斜边比上对边
小心中国借机开战占领整个南海