和差化积公式的推导 高一数学学习公式定理大全(5)

若通项公式变形为an=a1/q*q^n(n?N*),当q,0时，则可把an 前n项和公式为:Sn=na1+n(n-1)d/2或Sn=(a1+an)n/2 看作自变量n的函数，点(n,an)是曲线y=a1/q*q^x上的一群孤立的 若m+n=p+q则:存在am+an=ap+aq 点。 若m+n=2p则:am+an=2ap

(2) 任意两项am，an的关系为an=am?q^(n-m) 以上n均为正整数

(3)从等比数列的定义、通项公式、前n项和公式可以推出: 文字翻译

a1?an=a2?an-1=a3?an-2=„=ak?an-k+1，k?{1,2,„,n} 第n项的值=首项+(项数-1)*公差

(4)等比中项:aq?ap=ar^2，ar则为ap，aq等比中项。和差化积公式的推导 前n项的和=(首项+末项)*项数/2

记πn=a1?a2„an，则有π2n-1=(an)2n-1，π2n+1=(an+1)2n+1 公差=后项-前项

另外，一个各项均为正数的等比数列各项取同底数数后构成一个

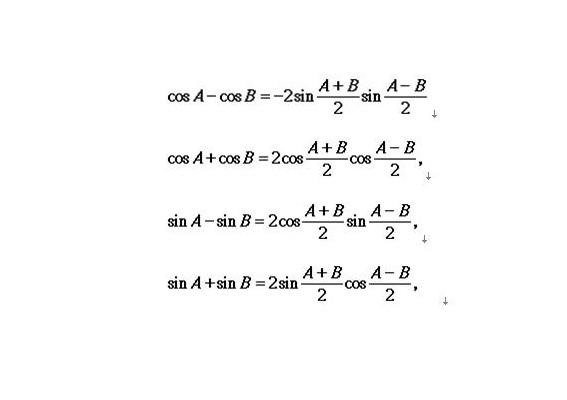
对称数列公式 等差数列;反之，以任一个正数C为底，用一个等差数列的各项做指

数构造幂Can，则是等比数列。在这个意义下，我们说:一个正项等

对称数列的通项公式: 比数列与等差数列是“同构”的。

对称数列总的项数个数:用字母s表示 性质:

对称数列中项:用字母C表示 ?若 m、n、p、q?N*，且m，n=p，q，则am?an=ap?aq;

等差对称数列公差:用字母d表示 ?在等比数列中，依次每 k项之和仍成等比数列.

等比对称数列公比:用字母q表示 “G是a、b的等比中项”“G^2=ab(G?0)”.

设，k=(s+1)/2 (5) 等比数列前n项之和Sn=A1(1-q^n)/(1-q)或

Sn=(a1-an*q)/(1-q)(q?1) Sn=n*a1 (q=1) 一般数列的通项求法

在等比数列中，首项A1与公比q都不为零.

注意:上述公式中A^n表示A的n次方。 一般有:

等比数列在生活中也是常常运用的。 an=Sn-Sn-1 (n?2)

如:银行有一种支付利息的方式---复利。 累和法(an-an-1=... an-1 - an-2=... a2-a1=...将以上各项

即把前一期的利息和本金加在一起算作本金， 相加可得an)。

再计算下一期的利息，也就是人们通常说的利滚利。 逐商全乘法(对于后一项与前一项商中含有未知数的数列)。

按照复利计算本利和的公式:本利和=本金*(1+利率)^存期 化归法(将数列变形，使原数列的倒数或与某同一常数的和成等

差或等比数列)。

等差数列公式 特别的:

在等差数列中，总有Sn S2n-Sn S3n-S2n 等差数列的通项公式为:an=a1+(n-1)d 2(S2n-Sn)=(S3n-S2n)+Sn 或an=am+(n-m)d 即三者是等差数列,同样在等比数列中。三者成等比数列

不动点法(常用于分式的通项递推关系) 还有以下的求和方法: 1,不完全归纳法 2 累加法 3 倒序相加法

特殊数列的通项的写法 (二)1.等比数列:

通项公式 an=a1*q^(n-1)(即q的n-1次方) a1为首项,an为第n

1,2,3,4,5,6,7,8....... ---------an=n 项

1,1/2,1/3,1/4,1/5,1/6,1/7,1/8......-------an=1/n an=a1*q^(n-1),am=a1*q^(m-1)