【每日一题】高中数学《对数函数及其性质》

【每日一题】高中数学《对数函数及其性质》

高中数学《对数函数及其性质》讲义

各位考官，我是今天的考生X，今天我的课的题目是“对数函数及其性质”。

新课程标准指出，高中教育属于基础教育，是基础性的对数函数教案下载，具有多样性和选择性，使不同的学生在数学上有不同的发展。今天，我将贯彻这一理念，从教材分析、学习情况分析、教学过程等方面开始我的讲座。

一、教材

首先说一下我对教材的理解。

对数函数的概念和性质是人民教育版A必修课第2章的内容。本课重点介绍对数函数的概念、对数函数的形象和性质。前面的学生学习了函数的概念，也探索了指数函数的概念、图形和性质。之前的学习对本课的知识和经验起到了铺垫的作用。从学生已有的知识和经验出发，引导学生发现问题和解决问题，对于进一步综合运用初等函数解决生产、生活和科研中的问题具有重要作用。

2.谈学习

对学业情况的合理把握，是一堂好课的基础。先说一下学生的实际情况。

高中生掌握了一定的解决问题的基本知识和经验，具有良好的分析和解决问题的能力。基于此，本课着重引导学生动脑思考，更有启发性。引导学生思考、总结，充分参与教学过程对数函数教案下载，进一步培养学生发现、分析和解决问题的能力。

三、教学目标

基于以上对教材的分析和对学习情况的把握，我制定了以下三个维度的教学目标：

(1) 知识和技能

掌握对数函数的概念，能够绘制对数函数的图形，根据对数函数的图形理解对数函数的性质。

(2) 过程和方法

通过探索对数函数性质的过程，学生可以体验到从特殊方法到一般方法以及数与形相结合的数学思维方法。

(3) 情感态度和价值观

通过本节的学习，体验数学的严谨性，养成仔细观察、认真分析、严谨思考的良好思维习惯。

四、谈教学难点

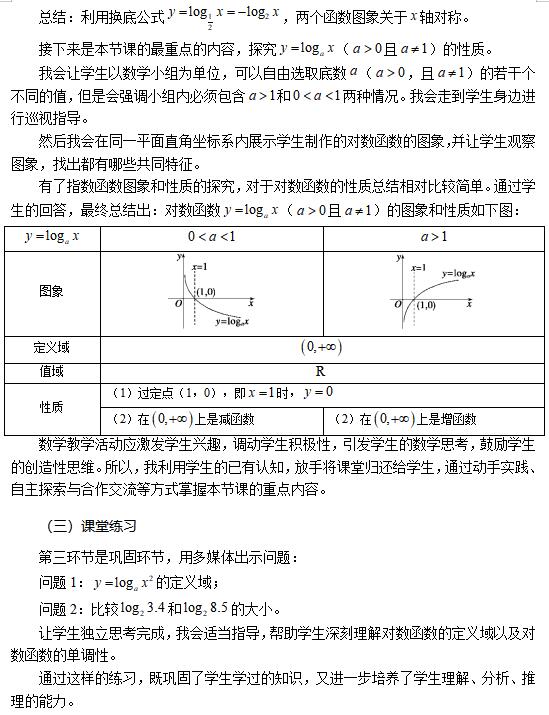
我觉得一堂好的数学课一定要在教学内容上突出重点，突破难点。教学重点的确立，肯定和我的课堂内容是分不开的。然后根据教学内容确定本课的教学重点：对数函数的概念、形象和性质。教学难点是：通过对数函数的图形归纳对数函数的性质。

5. 讲道和学习

现代教学理论认为，在教学过程中，学生是主体，教师是主导，教师是学习的组织者、引导者和伙伴。一切教学活动都必须注重强调学生的主动性和积极性。结合本课的内容特点和学生的年龄特点，本课我将采用讲授法、实践法、小组讨论法等教学方法。

6.谈谈教学过程

在这堂课的教学过程中，我注重突出重点，清晰、紧凑、合理。各种活动的安排也注重互动交流，最大限度地发挥学生参与课堂的积极性和主动性。

(1) 引入一个新的类

【每日一题】反函数与对数函数内在的对称统一教学

《对数函数教案253新人教学版A必修1.doc》为会员分享，可在线阅读。更多相关《对数函数教案253新人教学版A必修1.doc（5页珍藏版）》，请参考图书馆在线搜索。

1.课题：2.2.2对数函数（3）教学目标：知识与技能理解指数函数与对数函数的依赖关系，理解反函数的概念，加深对思想的过程和方法的理解功能建模。图，体验两个函数的单调性、情感、态度、价值观的异同，实现指数函数和对数函数的内在对称性和统一性程序和链接设计：创设情境、组织、探索，尝试练习，巩固，反思功课，回馈课外活动，从函数的角度分析例子，引入反函数的概念。从性质和相关性的角度来看，尝试简要总结指数函数和对数函数的定义、图形和性质。简单反函数问题和单调性问题是互为反函数的函数图之间的关系。教学过程

2、设计与操作：链接呈现教材、师生互动设计、情景素材1：当生物死亡时，其体内原有的碳14会按照一定的规律衰减，衰减到一半每 5730 年恢复其原始价值。这个时间被称为“半衰期”。根据一些规律，人们得到了生物体碳14含量P与生物体死亡年数t的关系。回答下列问题： (1) 求生物体死亡 t 年后的碳 14 含量。P，并从函数的角度解释P和t的关系，指出我们学到了什么样的函数？(2) 假设一个有机体中碳 14 的残留量为 P，求该有机体的年数 t' s 死亡，并用泛函的观点来解释 P 和 t 的关系对数函数教案下载，指出我们学到了什么样的函数？(3) 这两个函数之间有什么特殊关系？(4) P和t在映射上的对应关系是什么？(5) 特此您

3、可以获得什么样的灵感？学生：完成独立思考，讨论展示分析自己的结果教师：引导学生分析总结对数函数教案下载，得出结论：（1）P和t的对应关系是一一对应的；(2) P 是关于 t 函数的索引；t 是关于 P 的对数函数，它们的底相同。描述的是碳14衰变过程中碳14含量P与死亡年数t的对应关系；（3）本题同底 指数函数和对数函数是不同的数学模型，描述的是同一个关系（碳14含量P与死亡年数t的对应关系）。

4. -3-2-101231248 表2 -3-2-101231248 在同一坐标系下，用画点的方法绘制图像，然后引出反函数组织的概念。探索资料1：反函数的概念：当一个函数是一一映射时，这个函数的因变量可以作为一个新函数的自变量，这个函数的自变量可以作为一个新函数的自变量作为一个新功能。函数的因变量 图和函数的属性之间有什么特殊关系？师：解释：（1）互为反函数的两个函数是定义域和值域互换的两个函数，对应的规律互为逆；(2) 从反函数的概念，

有 f (ab) = f ( a ) + f ( b )”，你能说出这些函数有什么共同点吗？(2) 尝试列举几个满足“对于定义域中的任何实数 a 和 b，有 f

为什么？问题3 如果P0(x0,y0)在函数图上，那么P0关于函数图上直线的对称点是什么，为什么？?问题4 从上述查询过程可以得出什么结论？问题 5 上述结论对指数函数及其反函数是否成立？为什么？结论：互为反函数的两个函数的图关于直线对称