速率陀螺仪和积分电路 稳定系统中惯性MEMS的频率响应(3)

H1 = tf(NUM1,DEN1); % transfer function for first pole

H2 = tf(NUM2,DEN2); % transfer function for second pole

H488a = H1 * H2; % transfer function for 2-pole filter

[maga,phasea] = bode(H488,w);

for f = 1:Fmax

Mag488a(f) = maga(1,1,f);

Phase488a(f) = phasea(1,1,f);

end

为快速评估与这些滤波器相关的时间延迟，请注意单极滤波器的相位延迟在??3 dB频率下等于45°，也就是转折频率周期的1/8。在此情况下，加速度计的滤波器的时间延迟大约等于0.38 ms。对于陀螺仪，延迟等于两级的时间延迟的总和，约为0.47 ms。

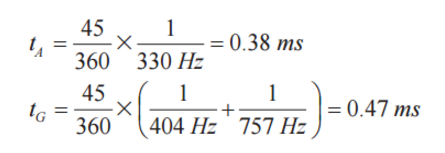
均值/抽取滤波器级

图3说明了两个均值/抽取滤波器级的使用，它们可以降低级的输出采样速率，并且提供额外的滤波。在具有有限脉冲响应(FIR)的数字滤波器中，相位延迟等于总抽头数的一半，除以每个抽头的采样速率。在第一个滤波级，采样速率为9.84 kHz。有四个抽头，在此种类型的滤波器中，这个数字等于均值数量。相位延迟约为0.2 ms。均值滤波器的幅度响应遵循这种关系

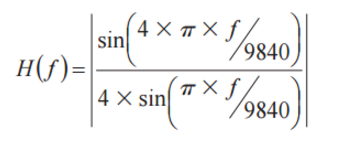
使用MATLAB进行分析时，请使用9.84 kSPS的采样速率(fs)和4个抽头(N)，以及用于分析模拟滤波器的相同频率数组(N)。使用相同频率数组，可以更加简单地组合每级的结果。请使用以下代码来分析第一级：

Fmax = 9840/2; % one-half of the sample rate

f = 1:Fmax;

NUM(f) = sin(4*pi*f/9840);

DEN(f) = 4 * sin(pi*f/9840);

for fq = 1:Fmax

Hda(fq) = abs(NUM(fq)/DEN(fq));

end

要分析第二个均值/抽取滤波器，需要事先了解控制系统的采样速率，但应使用相同的关系。例如，如果控制环路需要接近400 SPS的采样速率，则第二个滤波器的均值和抽取率将等于6（采样速率为410 SPS，有四个样本，因此为9840/[410 × 4] = 6）。使用相同的m-脚本代码可分析幅度响应，有三个例外：(1) 将采样速率从9480更改为2460；(2) 将两个位置的"4"更改为"6"；以及 (3) 将FMAX从9840/2更改为2460/2。相位等于总抽头数的一半，除以采样速率，约为1.22 ms (3/2460)。

复合响应

图4和图5提供了复合幅度和相位响应，包括陀螺仪的模拟滤波器和两个抽取滤波器。图4表示针对数组中的每个频率，将各级的幅度相乘的结果。图5表示将每个频率下的各级的相位贡献相加的结果。标记"没有抽取"的坐标图假定输出数据速率为2460 SPS，第二个抽取滤波器级有效关闭。标记"有抽取"的坐标图假定抽取率等于6，最终输出数据速率为410 SPS。两个坐标图说明了响应差异，帮助实现控制环路采样速率和相应频率响应的系统级平衡。

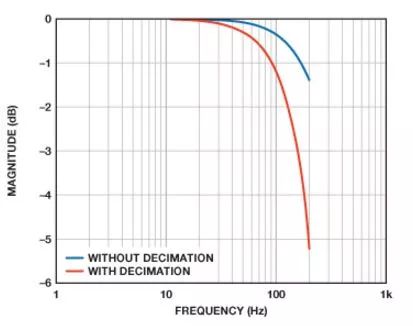
图4. 模拟滤波器和第一个抽取滤波器级

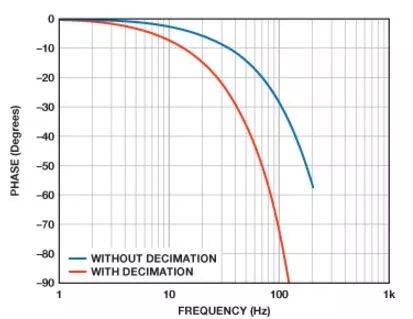
图5. 410-SPS数据速率的复合响应

可编程FIR滤波器分析

知道模拟滤波器和抽取滤波器的贡献之后，我们可以评估使用片内抽取滤波器和设计自定义FIR滤波器之间的比较权衡。在图3所示的ADIS16488中，FIR滤波器包括在IMU中，但有些系统在数字信号处理程序中实施滤波器。FIR滤波器的时域f(n) 以差分方程表示，其中z变换提供了用于频率分析的分析工具：