对数函数教案下载(【课题】4.4.1对数函数的图像及其性质【教材内容解析】)

[项目]4. 4.1 对数函数的形象及其性质 [教材内容分析] 1.《对数函数形象及其性质》是国家中等职业教育课程改革新规划教材，第四期章节“指数函数和对数函数”一章的重点内容。在此之前，学生已经对函数、域、取值范围等相关概念，以及函数的单调性、奇偶性等函数性质有一定的理解和掌握。同时，这节课是刚学完对数和指数函数后对对数函数的进一步学习。也是学生进一步理解函数学习方法的一种方式，即“概念-图像-自然-应用”的过程。同时，为以下功能的学习做铺垫。 2.“对数函数”是基本初等函数之一。对数函数的知识广泛应用于其他章节和其他学科。同时，对数函数作为一种常用的数学模型，在解决社会生活问题（统计、规划）方面也有着广泛的应用。本课的学习为学生提供了进一步学习、参与生产和实际生活所必需的基本数学技能。同时，本课对对数函数性质的研究，不仅体现了对数函数与指数函数的关系，还包含函数、数形组合等数学思想，也是一种高考重点内容。 【学生学业分析】 1、心理和生理：中职一年级学生在校已经两个月了，现在处于相对稳定的时期，所以他们的学习情绪和态度也比较稳定。此外，进入学校不久，学生的求知欲和学习欲望也空前高涨，积极主动，不怕吃苦。

2.知识：从初中到现在，学生学习了初等函数、反比例函数、二次函数、幂函数、指数函数等初等函数，对函数的概念和学习函数的方法有一定的了解。理解和掌握，再加上对数和指数的关系，学生已经明白可以通过类比来学习和学习，对数函数的应用在数学和日常生活中都有广泛的应用。因此，自然而然地激发了学生学习这节课的积极性和兴趣。 【教学目标】知识目标：（1）了解对数函数的形象和性质；（2）掌握对数函数的单调性，会比较同底的对数和不同底的对数，加深理解对数函数和指数函数的本质。能力目标：观察对数函数的形象，总结对数函数的本质，培养观察能力。情感目标：（1）体味）对数函数，养成严谨的思维习惯；（2）参与数学建模的过程，感受生活中的数学模型，体验数学知识的应用。【教学重点】（1）对数函数形象与性质； （2）对数函数性质的初步应用，利用对数函数的单调性来比较同底对数的大小。【教学难点】底数 a 对对数函数性质的影响。 【教学设计】 ⑴ 举例介绍知识，增强学生的好奇心； ⑵““指点法”绘图与软件应用相结合对数函数教案下载，有助于观察指数函数的性质； ⑶巩固和实践知识，培养学生的思维能力；⑷解决实际问题，培养学生分析和解决问题的能力; ⑸ 以小组形式讨论、询问、交流、培养团队精神 [教学设备] 教学课件、多媒体 [课程安排] 1 课时（45 分钟） [教学过程] 教学过程的教学意向时间*揭秘topic4.4 对数函数。 *创建情境兴趣导入器：新课开始前，先复习一下相关知识。

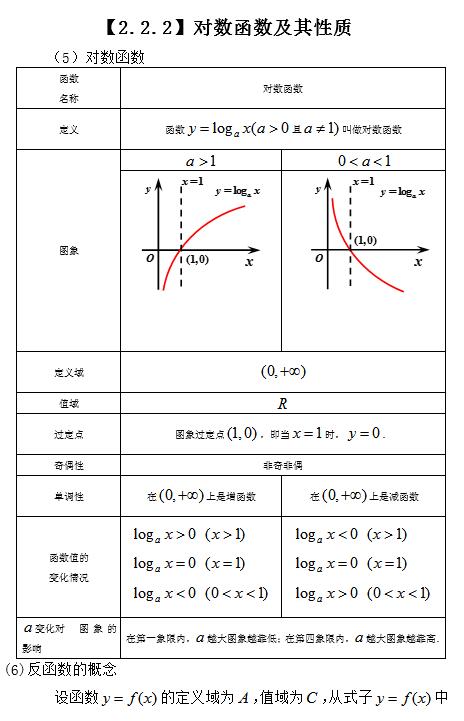
指数和对数的等价关系是什么？怀孕：。师：每个字母的取值范围是多少？健康：a>0a≠1； N>0； εR。师：什么是指数函数？学生：函数（a>0a≠1）称为指数函数。老师：指数函数的定义域和范围是什么？学生：定义域是R，范围老师：对数函数的概念？学生: 一般而言，Function, (a>0 and a≠1)称为对数函数，其中定义域为(0, +∞)* 头脑风暴，探索新概念。一般形式的函数称为对数函数有底，其中a>0且a≠1。对数函数的定义域为R。例如，和都是对数函数。体验指数函数特性的指南。图像。函数的定义域为取x的一些值，列表如下： x…124…-2-1012…210-1-2…取表中x的值和函数对应的y值作为坐标，绘制 用平滑曲线依次连接各个点对数函数教案下载，得到函数的图像；取表4-6中x的值和y的值 cor以函数为坐标，追踪点，依次用平滑曲线连接点，得到函数的图像，如下图： 观察函数图像，发现： 1.图像函数和图像位于 x 轴的右侧； 2.图像通过点； 3、功能形象从左到右有上升趋势；函数的图像从左到右呈上升趋势。下降趋势。复习绘图点作为函数图像的方法的计算部分可以由学生完成，引导学生观察函数图像的特点。 （1）函数的定义域为R；（2）当时的函数值；（3）当a>1，函数内部为递增函数；00时，定义域为;（2）由得，所以定义域是。通过样题进一步理解对数函数的域40*利用知识加强练习课本练习4.4.11。多项选择：（1）若函数图像 点后，底数 = (). A. 2B.? 2 CD (2） 下面的对数函数是 (0, +) 区间内的递减函数是 (). ABCD ．2. 令下列函数的图并判断它们的单调性。(1) ;(2) ．3. 求下列函数的域：(1）(2）师：如何求函数) 什么问题定义域时要注意什么？生：（1）分母不能为0；（2）偶次根，平方根的个数为非负数；（3）0的0次方为毫无意义。

老师：还有其他限制吗？生：对数的真实数大于0。 师：好的，我们现在看这道题。其实就是考察对数函数的域。与底无关，只要真数大于0即可。如果对数的底相同，则直接用对数函数的单调性进行比较；如果底数和真数都不一样，就用中间量作为桥梁，比较中间量和两个对数公式的大小。公式的大小。通常引入中间变量 1 或 0。 *课堂总结正确理解对数函数的定义；掌握对数函数的形象和性质；能够利用对数函数的性质解决相关问题。问题类型： 1. 查找域； 2. 比较两个对数表达式之间的关系。注：1.模拟记忆指数函数和对数函数； 2.看到功能，想一想形象，结合形象的本质。 * 布置作业 1. p82 # 7; p83 #8. *黑板设计，及时了解学生的知识和掌握情况 45* 评价与分析 本课以功能性自然探索课为主，辅以独立探索、讨论和总结，以及简单的自然应用练习。因此，本节将从以下几个环节进行评价：1.采用对数函数图像的绘制方法，考察学生对函数学习的一般方法和思维多样性评价的掌握情况； 2.通过简单例子的解答来评估学生运用知识解决问题的能力； 3.评估学生解决问题的能力，激发对自然的深入理解，通过布置作业来解决更复杂的问题。 **高质量的教案(1,0）0(1, 0）0

)

教案网123