《横和竖的书写》教学设计教学目标(图)

《横和竖的书写》教学设计教学目标(图)

“横向和纵向写作”教学设计教学目标

1.让学生掌握水平和垂直两个基本笔画，包括开始和合笔

2.写“二”、“三”、“十”、“”

工作“等，用这两个基本笔画，并注意新字中的横竖书写方式

3、培养学生细心观察的素质，规范先写后写后评价的习惯，在写作过程中渗透到美育中

4、培养良好的写作姿势和写作方法书法教案竖画模板，激发学生对写作的热爱和兴趣，教出难点，学生能掌握横竖书写法两个基本笔画，教学准备，场外字网格，练习纸教学时间，第一课教学过程

1. 课前乐趣

1.今天我们要学习“一”和“我”，两个基本的笔画，水平和垂直（全班一起读题目）。

2.复习《写歌》，一边随着节奏拍手一边唱

3、复习书写姿势，学生纠正姿势，老师示范纠正

2. 学习新课程

4.查看字段网格的位置，强调

重视观察岗位，强调写作姿态

5.大屏幕显示长短“一”

6.课堂交流起笔合笔的重要性，长短横写有哪些特点

3.指导写作长横短横写

1.老师写长“一”和短“一”，学生观察结构

2.学生然后在作业纸上写三个长“一”和三个短“一”，指出写作要领，横线方向略微向上

3. 命名董事会的表现和评论

5、全班练习写三长横笔、三短横笔

4.用横字引导字的书写

6. 在大屏幕上呈现

二、三

7. 指导观察入住情况

8.在同一张桌子上写模仿和评论

9.点名板表现，复习10个全班练习写作”

二、三、三

5.指导写作《|

1.大屏幕显示垂直和挂针垂直2、课堂传达起笔

合笔的重要性，以及竖针和挂针的特点，指导写作要领

3.老师写竖挂针，学生观察结构

4、全班练习写三竖三挂针

6.指导书写竖笔，挂针竖笔，注意竖笔，合笔

重，挂针竖笔重，合笔轻

1. 命名板绩效评估

2、全班练习写三竖挂针、三竖挂针

7.指导横竖字字的书写

1.呈现在大屏幕上”

10.工作，干燥，土壤”

2.引导观察入住

3.在同一张桌子上写模仿和评论

4. 命名板绩效考核

5.全班练习写作”

10.工作、干燥和土壤“各是三个

8.课间活动手指练习，手腕运动，促进手指的和谐操作

9. 课程总结 我们的汉字有一种刚性、柔和的美感，希望大家通过练习写出漂亮的汉字，做出有尊严的汉字

10.板书横竖 《横竖写》说教材是陈家湾小学王琳琳写的

一、教学内容：写作教学在小学语文教学中占据主导地位，如何教写作教学，如何教孩子如何写作非常重要，本课程的教学目的是让学生在轻松愉快的氛围中“基本笔画一个一个，横竖”， 结合教学，让学生掌握横向和纵向写作的要点，培养学生观察和规范写作的能力2、教学

与学习方法：本课充分发挥学生主动学习的原则，在课堂上为学生营造轻松和谐的教学氛围，使学生喜欢写作、愿意写作，并将现有经验转化为有效的课堂资源，学会观察、学会发现、养成良好的写作习惯

三、说教学目标

1.让学生掌握水平和垂直两个基本笔画，包括开始和合笔

2.写“二”、“三”、“十”、“”

工作“等，用这两个基本笔画，并注意新字中的横竖书写方式

3、培养学生细心观察的素质，规范先写后写后评价的习惯书法教案竖画模板，在写作过程中渗透到美育中

4、培养良好的写作姿势和写作方法，激发学生对写作的热爱和兴趣

四、谈教学过程

1. 课前乐趣

1.今天我们要学习“一”和“我”，两个基本的笔画，水平和垂直（全班一起读题目）。

2.复习《写歌》，一边随着节奏拍手一边唱

3、复习书写姿势，学生纠正姿势，老师示范纠正

二、学习新课 2、复习田子网格的位置，强调观察位置的重要性，强调写作姿势

4.大屏幕显示长短“一”

5.课堂交流起笔合笔的重要性，长短横写的特点是什么

3.指导写作长横短横写

1.老师写长“一”和短“一”，学生观察结构

2.学生然后在作业纸上写三个长“一”和三个短“一”，指出写作要领，横线方向略微向上

3. 命名董事会的表现和评论

5、全班练习写三长横笔、三短横笔

4.用横字引导字的书写

1.大屏幕演示

二、三

2.引导观察入住

3.在同一张桌子上写模仿和评论

4. 命名板性能，审查

5.全班练习写作”

二、三、三

5.指导写作《|

1.大屏幕显示垂直和挂针垂直2、课堂传达起笔

合笔的重要性，以及竖针和挂针的特点，指导写作要领

3.老师写竖挂针，学生观察结构

4、全班练习写三竖三挂针

6.指导书写竖笔，挂针竖笔，注意竖笔，合笔

重，挂针竖笔重，合笔轻

1. 命名板绩效评估

2、全班练习写三竖挂针、三竖挂针

7、横竖字L大屏书写指导”

10.工作，干燥，土壤”

3.指导观察入住情况

4.写模仿和评论在同一桌

5. 命名板绩效评估

6.全班练习写作”

10.工作、干燥和土壤“各是三个

8.课间活动手指练习，手腕运动，促进手指的和谐操作

9. 课程总结 我们的汉字有一种刚性、柔和的美感，希望大家通过练习写出漂亮的汉字，做出有尊严的汉字

10.板书是水平和垂直的。

【每日一题】平行四边形互相平分可得点O，一条学生的克星

三角形重心的表现——2022年上海中考数学25题

在教学过程中，我最怕遇到这样的学生。他们一看到某张图，还没看完题情，就给它加上辅助线。如果他们做对了，他们会告诉我等腰三角形知识点及典型习题教案模板3，这道题太简单了，一下子就出来了某个模型；做不好就开始尝试各种机型的辅助线加法，直到遇到死老鼠；我别无选择，只能徒劳地消耗自己而死。

那些看起来像模型，却不用模型套路的期末题，正是这类学生的克星。

话题

平行四边形ABCD，若P为BC的中点，则AP与BD相交于E点，并连接CE。

(1) 如果 AE=CE。

①证明：平行四边形ABCD是菱形；

②若AB=5，AE=3，求线段BD的长度；

(2) 以A为圆心，AE为半径作圆，以B为圆心等腰三角形知识点及典型习题教案模板3，BE为半径作圆，两圆的另​​一交点记为F点，CE=√2AE ，如果F在CE直线上，求AB：BC的值。

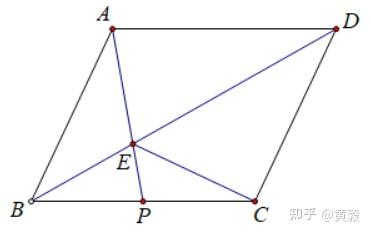
解析：

(1) 给定条件AE=CE，原来的平行四边形ABCD的形状发生了变化，如下图所示：

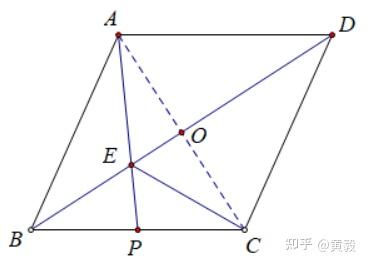
①连接AC，由AE=CE可知△AEC是等腰三角形，然后平行四边形的对角线相互平分得到O点是AC的中点，最后结合三条线证明OE⊥BD ，即AC⊥BD，现在平行四边形ABCD的对角线互相垂直，所以是菱形；

②根据上面证明的菱形，观察AB和AE。它们的共同点是都是直角三角形的斜边，分别为Rt△AOB和Rt△AOE。同时，这两个三角形还有一条公共边OA，另一条直角边在BD上，这让人联想到勾股定理，如下图所示：

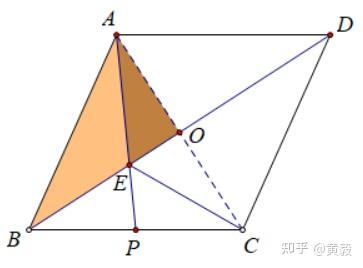
在Rt△AOB中，OA²=AB²-OB²=25-OB²，在Rt△AOE中，OA²=AE²-OE²=9-OE²，我们可以得到25-OB²=9-OE²，我们整理一下：

OB²-OE²=16

(产科+手术室)(产科-手术室)=16

至此，OB与OE之间是否存在数量关系？

再考察△ABC，AP是它的中线，BO也是中线，两条中线相交，交点就是重心。如果你能想到重心的性质，它会把每条中线分成1:2的两部分，这道题就容易了；

BE=2OE由重心性质可得，故OB=3OE，上式可改为8OE²=16，可解OE=√2，故OB=3√2，BD=6 √2;

为什么重心可以把每条中线分成1:2的两部分呢？我们可以用面积法来证明：

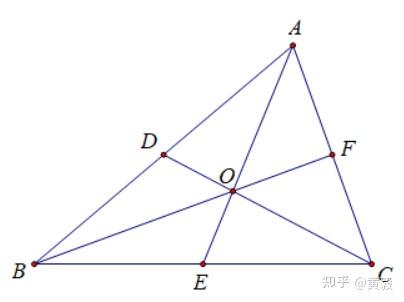
上图中，△ABC的三条中线相交于O点，每条中线将△ABC分成面积相等的两部分。例如，△ABE 和△ACE 的面积相等。同样，对于△OBC，OE也是它的中线，所以△OBE如果△OCE的面积等于△AOB的面积，则△AOB和△AOC的面积相等。可以证明，上图中6个小三角形的面积都是相等的，其中△AOB占1/3，△OBE占1/6。它们高度相等，所以底部的比例为2:1，即OA:OE=2:1，其余同理证明；

(2)我们先根据题目的要求画一张图，如下：

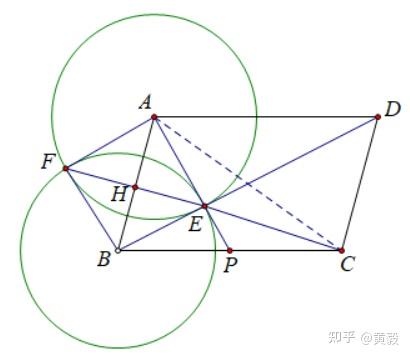
其实这两个圈子的作用，主要是为了引起大众对EF的关注。由于教科书上没有给出公共和弦的性质，所以需要一个简单的证明；

在圆A中，AE=AF，在圆B中，BE=BF，A点和B点到线段EF两端的距离相等，所以AB是EF的垂直平分线。

之前已经证明了△ABC的重心是E点，在这个小问题中依然成立，所以CH也是△ABC的中线，即H点是AB的中点，现在AB与EF相互垂直，即四边形AFBE为菱形；

现在我们不需要那两个圆圈了，我们把重点放在用好这个菱形上，如下图所示：

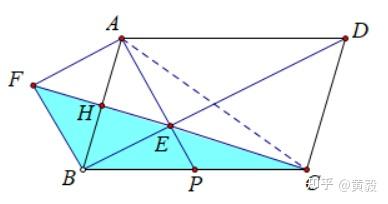
△BCF中，点P为BC边的中点，PE∥BF，可得PE为△BCF的中线，令AE=x，则CE=√2x，则EF=√2x，EH =√2/2·x，现在看△AEH，显然这是一个等腰直角三角形，求AH=√2/2·x，则AB=√2x；

在Rt△BCH中，我们利用勾股定理得到BC²=BH²+CH²，其中BH=√2/2 x，CH=3√2/2 x，BC=√5x；

最后求出AB:BC=√10/5。

解题反思：

这个几何结局还是有难度的。要理解的关键点是三角形重心的性质。当我们了解三角形的重心时，印象最深的就是它是三条中线的交点。切分，如果接触少了，就不太记得了，尤其是第二个小题，判断点H也是AB的中点。

当然，这道题讲完之后，我会觉得这么简单，重点都知道了，为什么做题的时候就想不到呢？让我们回到重心部分的内容。课本上对它的描述是什么？能否纳入课本习题？它是如何使用的？为什么我们在平时的作业或考试中不能这样考呢？就因为我平时不这样考试，难道我不这么认为吗？...

对于一系列的问题，我一定是找到了部分原因。初中数学的知识点很多。他们已经被实践和总结，但不能变成套路。了解每个模型的本质，知道它为什么成为模型是非常重要的。

还是那句话，我对解题模式没有异议，但是如果是学生自己总结出来的，老师是灌输不了的。如果把解题模型看成是一门武功，那么最高境界应该是“无招以招取胜”。