等腰三角形知识点及典型习题教案模板3(【衡实教育】初中数学人教2011课标版教学目标)

张晓娜

地区：吉林省-吉林市-舒兰市

学校：树兰第二十中

总共1小时

13.3 等腰三角形初中数学教学2011标准版

1 教学目标

1.知识与技能：了解等腰三角形的概念，探索和掌握等腰三角形的性质；

2.数学思维：通过观察、实验、探究、归纳、推理、证明，让学生体验认识图的全过程，理解实验几何与论证几何的有机结合；

3.解题：通过对等腰三角形性质的研究，让学生认识到实验几何的重要性，培养学生的直觉思维和创造性思维。可以利用属性进行相关的推理论证；

4.情感态度与价值观：通过剪纸等活动，培养学生的实验意识和探索精神，让学生进一步认识数学与现实生活的紧密联系，感受数学的严谨和结果的确定性。

2 学业情况分析

“13.3个等腰三角形(1）”摘自《人民教育版》八年级数学上册第十三章第三节。本课是在基础上进行的本课程的标准要求是让学习者了解等腰三角形的概念，能够识别等腰三角形，标注等腰三角形的元素，理解等腰三角形的性质和性质的推导过程，并能能够运用性质解决简单的问题，旨在培养学生的推理能力和解题步骤的完整性和规范性。

学生是课堂学习的主要参与者。要给学生留足时间，努力为学生营造一种自由探索创新的氛围，让学生感受到学习带来的快乐。根据中学生的心理特点和身心发展规律，利用学生对未知知识的好奇心，引导学生建立未知知识与已有知识的联系，使学生实现自我建构的过程. 建构主义理论表明，知识学习是学生自我建构的过程。

3个关键点

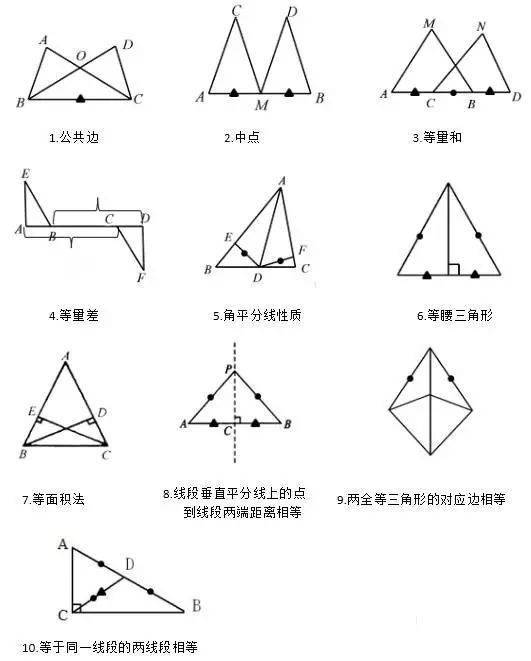
要点：等腰三角形的两个底角相等，具有“三线合一”的性质

难点：等腰三角形性质的证明与应用

4 教学过程4.1 第一课时教学活动活动一【导入】活动一：多媒体课件展示等腰三角形图片并进行场景导入

让学生仔细观察图片，发现它们的共同特征，复习和总结等腰三角形的定义

活动二【教学】活动二：动手操作

如图，将一张长方形的纸按照图中虚线对折，剪掉阴影部分，再次展开。

教师指导学生折叠和剪纸。

问题1.得到的△ABC有什么特点？

学生观察和发现

教师根据学生的结论定义等腰三角形、边、底、顶角和底角。

教师关注：1.学生在操作过程中的主动性和积极性；

2.你能发现三角形的特征吗？

设计意图：通过实验激励学生。亲身体验操作、实验、发现，认识数字与形状组合之美，体验成功的喜悦。

问题2.请在练习册上画（画）一个等腰三角形。陈述你的基础，并指出它的腰部、底边、顶角和底角。

学生：制作（画）图并回答相关问题。

师：巡导，重点看学生能不能画（画）等腰三角形，用什么方法。

设计意图：通过本次绘图（绘图）练习，加深学生对等腰三角形的理解，体验原始知识和生活基础在数学中的作用。

活动三【活动】活动三：观察发现属性

问题1.你刚才剪下来的等腰三角形在哪里，请判断是轴对称图形吗？

学生回答。教师注重学生参与的动机。

设计意图：在上面画（画）等腰三角形时，有些学生可能会觉得有点困难，甚至失去信心。通过这个问题点燃学生的积极性，调动积极性。

问题2.沿折痕对折剪下的等腰三角形ABC。指出它们重叠的线段和角度。

学生：反复对折等腰三角形，观察讨论得出结论，填入上表。

教师注重学生的合作意识和结果的正确性。

设计意图：进一步调动学生的积极性，在遇到困难时解决问题。为总结等腰三角形的性质奠定基础。

问题 3. 看看你填写的表格，你能找出等腰三角形的性质吗？告诉我你的猜测。

学生观察、总结并提出结论。教师及时引导（如指出：巧合相等），结合学生猜想，给出性质：

性质1.等腰三角形的两个底角相等（简称“等边到等角”）

属性2.等腰三角形的顶角平分线、底边中线、底边高重合

教师注重学生的语言概括能力。

设计意图：培养学生的归纳、概括和语言表达能力。

活动四【活动】活动四：小组讨论

师：上述性质是由有限个等腰三角形求得的。它对所有等腰三角形都有这个属性吗？这需要我们去证明。使用以下一系列问题来指导学生完成证明。

问题1.我们已经知道等腰三角形是轴对称图形。请观察等腰三角形被对称轴分成的两个三角形之间的关系是什么？

学生：△ABD≌△ACD

问题2.两个三角形全等可以得出什么结论？

学生：∠B=∠C；∠坏=∠CAD；∠ADB=∠ADC

BD=CD

问 3. ∠B=∠C 表示什么？

学生：等腰三角形的两个底角相等。

问 4. ∠BAD=∠CAD 表示AD是顶角的平分线吗？

∠ADB=∠ADC表示AD高？

BD=CD 是否意味着 AD 是中线？

师：现在证明等腰三角形的性质吗？请证明。

学生：独立完成的证明。老师们重点练习辅助线等腰三角形知识点及典型习题教案模板3，最后给出证明。

设计意图：在老师的指导下，逐步完成对自然的证明，让学生加深对辅助线的理解，培养学生完整的推理和证明能力。

Activity 5 [Exercise] Activity 5：应用自然，解决问题

1、等腰三角形的底角为 70°，顶角为______。

2、等腰三角形的一个角是70°，另外两个角是

____________________。

3、等腰三角形的一个角是 110°，另外两个角是 ___________。

例如1、 如图，在△ABC中，AB=AC，D点在AC上，BD=BC=AD，求△ABC各角的度数。

例2、 已知：如图所示，房屋顶角为∠BAC=100º，穿过屋顶A的柱子为AD^BC，椽子AB=AC。求 ∠B, ∠C, ∠BAD, ∠ 在 CAD 的屋顶框架度数上。

设计意图：应用所学，解决简单问题，体现应用意识。

扩展改进：等腰三角形底中点到两侧的距离是否相等？

如图，DE⊥AB，DF⊥AC，竖脚分别为E，F。等腰三角形

沿对称轴AD折叠形状ABC等腰三角形知识点及典型习题教案模板3，观察DE和DF的关系。

活动六【作业】活动六：总结与作业

1.总结

请先把等腰三角形剪下来，然后和小组一起指出你所知道的。

学生在小组中解释他们学到了什么。教师对各组进行检查，指导学生补充和提高。

教师注重：①总结总结能力；②不同层次学生对本部分知识的理解程度；③学生独立面对和克服困难的能力。

设计意图：激发学生积极参与的意识，为每个学生创造在数学学习活动中体验成功的机会，为学生提供不同层次的充分展示自我的机会。

2.作业：

1.标题 8，第 151 页，1、3、

2.下一课预习（144 页）

13.3个等腰三角形

课时设计课记录

13.3个等腰三角形

1 第一课时教学活动活动一【导入】活动一：多媒体课件展示等腰三角形图片并进行场景导入

让学生仔细观察图片，发现它们的共同特征，复习和总结等腰三角形的定义

活动二【教学】活动二：动手操作

如图，将一张长方形的纸按照图中虚线对折，剪掉阴影部分，再次展开。

教师指导学生折叠和剪纸。

问题1.得到的△ABC有什么特点？

学生观察和发现

教师根据学生的结论定义等腰三角形、边、底、顶角和底角。

教师关注：1.学生在操作过程中的主动性和积极性；

2.你能发现三角形的特征吗？

设计意图：通过实验激励学生。亲身体验操作、实验、发现，认识数字与形状组合之美，体验成功的喜悦。

问题2.请在练习册上画（画）一个等腰三角形。陈述你的基础，并指出它的腰部、底边、顶角和底角。

学生：制作（画）图并回答相关问题。

师：巡导，重点看学生能不能画（画）等腰三角形，用什么方法。

设计意图：通过本次绘图（绘图）练习，加深学生对等腰三角形的理解，体验原始知识和生活基础在数学中的作用。

活动三【活动】活动三：观察发现属性

问题1.你刚才剪下来的等腰三角形在哪里，请判断是轴对称图形吗？

学生回答。教师注重学生参与的动机。

设计意图：在上面画（画）等腰三角形时，有些学生可能会觉得有点困难，甚至失去信心。通过这个问题点燃学生的积极性，调动积极性。

问题2.沿折痕对折剪下的等腰三角形ABC。指出它们重叠的线段和角度。

学生：反复对折等腰三角形，观察讨论得出结论，填入上表。

教师注重学生的合作意识和结果的正确性。

设计意图：进一步调动学生的积极性，在遇到困难时解决问题。为总结等腰三角形的性质奠定基础。

问题 3. 看看你填写的表格，你能找出等腰三角形的性质吗？告诉我你的猜测。

学生观察、总结并提出结论。教师及时引导（如指出：巧合相等），结合学生猜想，给出性质：

性质1.等腰三角形的两个底角相等（简称“等边到等角”）

属性2.等腰三角形的顶角平分线、底边中线、底边高重合

教师注重学生的语言概括能力。

设计意图：培养学生的归纳、概括和语言表达能力。

活动四【活动】活动四：小组讨论

师：上述性质是由有限个等腰三角形求得的。它对所有等腰三角形都有这个属性吗？这需要我们去证明。使用以下一系列问题来指导学生完成证明。

问题1.我们已经知道等腰三角形是轴对称图形。请观察等腰三角形被对称轴分成的两个三角形之间的关系是什么？

学生：△ABD≌△ACD

问题2.两个三角形全等可以得出什么结论？

学生：∠B=∠C；∠坏=∠CAD；∠ADB=∠ADC

BD=CD

问 3. ∠B=∠C 表示什么？

学生：等腰三角形的两个底角相等。

问 4. ∠BAD=∠CAD 表示AD是顶角的平分线吗？

∠ADB=∠ADC表示AD高？

BD=CD 是否意味着 AD 是中线？

师：现在证明等腰三角形的性质吗？请证明。

学生：独立完成的证明。老师们重点练习辅助线，最后给出证明。

设计意图：在老师的指导下，逐步完成对自然的证明，让学生加深对辅助线的理解，培养学生完整的推理和证明能力。

Activity 5 [Exercise] Activity 5：应用自然，解决问题

1、等腰三角形的底角为 70°，顶角为______。

2、等腰三角形的一个角是70°，另外两个角是

____________________。

3、等腰三角形的一个角是 110°，另外两个角是 ___________。

例如1、 如图，在△ABC中，AB=AC，D点在AC上，BD=BC=AD，求△ABC各角的度数。

例2、 已知：如图所示，房屋顶角为∠BAC=100º，穿过屋顶A的柱子为AD^BC，椽子AB=AC。求 ∠B, ∠C, ∠BAD, ∠ 在 CAD 的屋顶框架度数上。

设计意图：应用所学，解决简单问题，体现应用意识。

扩展改进：等腰三角形底中点到两侧的距离是否相等？

如图，DE⊥AB，DF⊥AC，竖脚分别为E，F。等腰三角形

沿对称轴AD折叠形状ABC，观察DE和DF的关系。

活动六【作业】活动六：总结与作业

1.总结

请先把等腰三角形剪下来，然后和小组一起指出你所知道的。

学生在小组中解释他们学到了什么。教师对各组进行检查，指导学生补充和提高。

教师注重：①总结总结能力；②不同层次学生对本部分知识的理解程度；③学生独立面对和克服困难的能力。

设计意图：激发学生积极参与的意识，为每个学生创造在数学学习活动中体验成功的机会，为学生提供不同层次的充分展示自我的机会。

2.作业：

1.标题 8，第 151 页，1、3、

2.下一课预习（144 页）