高中数学试讲教案模板(【每日一题】教师资格证《算法》练习题)

算法的意义

教学目标：通过对解决具体问题的过程和步骤的分析，理解和掌握算法的概念和意义，能够运用“算法”的思想为数学问题编写算法。

教学重点：通过实例体验算法思想，初步理解算法的含义。教学难点：算法的概念和算法的自然语言描述。课程类型：新教学法：多媒体教学流程：

一、创造情境

请研究解决以下问题： 1. 写下家里烧水的过程。一般第一步：往电锅里倒水；第二步：打开电源烧开水；第三步：将开水倒入保温瓶中。问题 2. 两个大人和两个孩子一起过河。渡轮上只有一艘小船，一次只能渡过一个大人或两个孩子。四个人都能划船，却没有一个人会游泳。他们是怎么过河的？请写一份过河的计划。（通过学生讨论高中数学试讲教案模板，过河的计划和步骤如下）

S1 两个孩子同船过河；S2 一个孩子划船回来；S3 划船过河的成年人；S4 对面的孩子向后划船；S5 两个孩子同船过河；S6 一个孩子划船回来；

S7 剩下的大人独自划过河；另一边的孩子向后划船；

S8 两个孩子同时划过河。

二、活动尝试

广义上讲，解决某一问题所采取的方法和步骤称为算法。做任何事情都有一定的步骤。例如，描述太极动作的图是《太极算法》；一首歌的乐谱可以称为这首歌的算法。从小学到高中遇到的算法，大部分都与“计算”问题有关。

三、师生研究

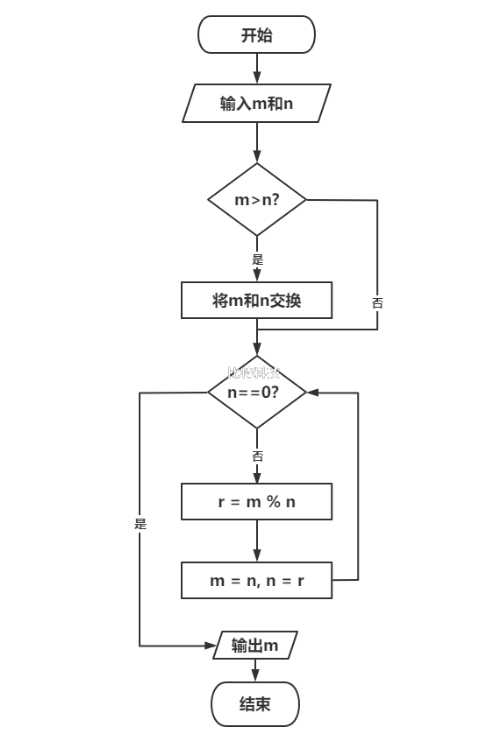
例 1：给出一个算法来找到 1+2+3+4+5。解：算法1按照一一相加的过程进行

第一步：计算1+2，得到3；

第二步：将第一步的运算结果3和3相加得到6；

第三步：将第二步的计算结果6和4相加得到10；

Step 4：将第三步运算结果的10和5相加得到15. 算法2 可以用公式1+2+3+„+n= Step 1：取n=5；

第 2 步：计算

n(n+1) 直接计算 2n(n+1); 2 第三步：输出运算结果。算法3按照累加程序进行

Step 1：令S=0，I=1 Step 2：将S+I的值赋给S，并将I的值加1。 Step 3：如果I大于5，则输出S，否则转步骤2. . （说明算法不只是一） 例2：（教科书第2页高中数学试讲教案模板，求解一个线性方程组在两个未知数中的步骤）

（可以推广到求解一般的二元线性方程组来说明算法的通用性）

四、数学理论

通过对以上问题的分析，我们对算法有了初步的了解。在解决某些问题时，需要设计一系列可操作或可计算的步骤，通过实现这些步骤来解决问题。步骤被称为算法来解决这些问题。在数学中，现代意义上的“算法”通常是指计算机可以解决的程序或步骤。这些程序或步骤必须清晰有效，并且可以在有限的步骤内完成。问题：我们要解决一类问题，我们可以抽象出解决问题的步骤或计算顺序，以及它们有什么。. . . . . 要求？

（1）算法与一般意义上的具体问题的解决方案相关又不同。它们有一般和特殊的关系，也有抽象和具体的关系。算法要借助具体问题在一般意义上的解决方法，任何具体问题都可以用这类问题的通用算法解决。（2）算法的五个特点

①有限性：一个算法的步序是有限的，在有限步运算后应该停止，不能无限执行。

②确定性：算法中的每一步都应该是确定性的，能够有效地执行并得到确定的结果，不能有歧义。

③逻辑：算法从初始步骤开始，分为若干清晰的步骤。上一步是下一步的前提。只有上一步执行完才能进行下一步，每一步都准确完成问题。

④ 非唯一性：解决某个问题的算法不一定是唯一的，可以有不同的算法。⑤通用性：许多具体问题可以通过设计合理的算法来解决，例如心算和计算器计算，必须通过有限的、预先设计的步骤来解决。

五、整合应用

示例 3：编写 1×2×3×4×5 的算法。

第一步：先求1×2，得到结果2；

第二步：将第一步得到的结果2乘以3得到6；

第三步：将第二步得到的结果6乘以4得到结果24；第四步：将第三步得到的结果24乘以5得到120。 例4：写出求整数a、b、c的最大值的算术解：S1首先假设序列中的第一个数字是\"最大值\”。

S2 将序列中的下一个整数值与“最大值”进行比较。如果大于“最大值”，则假定该数字为“最大值”。

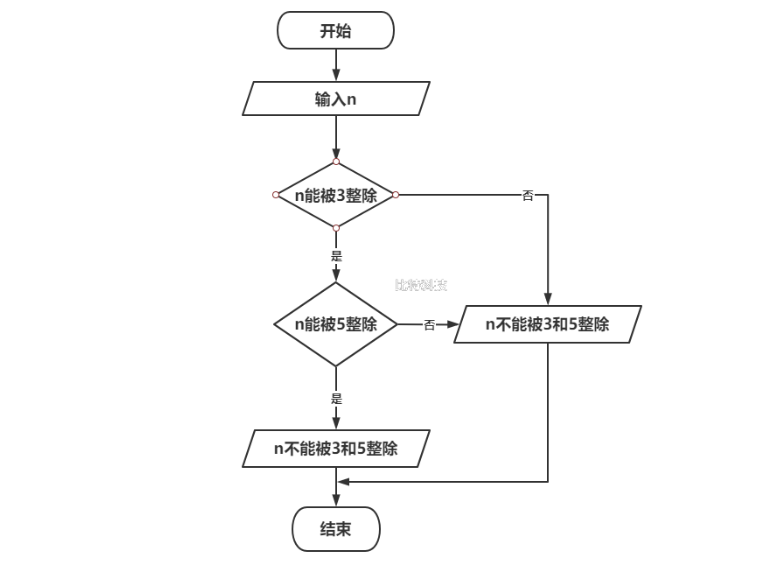
S3 如果序列中有其他整数，则重复 S2。

S4 直到序列中没有可比较的数字为止，此时假设的“最大值”就是序列的最大值。即，S1max=a。

S2 如果b>max，则max=b。S3 如果c>max，则max=c。S4 max 是a、b 和c 的最大值。

六、回顾与反思

1、算法定义：

算法可以理解为一个完整的解决问题的步骤，由基本操作和规定的操作顺序组成。或者作为根据需求设计的有限而精确的计算序列，这样的步骤和序列可以解决一类问题。

2、算法的五个特点：

⑴逻辑：算法应该是正确的和顺序的。算法从初始步骤开始，分为若干清晰的步骤。上一步是下一步的基础。执行完上一步后才能进行下一步。每一步都有明确的含义，构成了一个强大的逻辑序列。.

⑵通用性：算法必须能够解决一类问题，并且是可重用的。⑶ 有限性：必须保证一个算法在执行完有限步后结束

⑷ 非唯一性：解决某个问题的算法不一定是唯一的，一个问题可以有不同的算法。⑸ 通用性：很多问题可以通过设计合理的算法来解决。如：用二分法求方程的近似零点，求几何体的体积等。

3、 算法的表达形式：

⑴ 用日常语言和数学语言或借助形式语言（算法语言）进行精确的解释。⑵程序框图（简称框图）。⑶ 编程语言。

七、课后练习

1. 下列关于算法的叙述中，正确的是（ ） ①解决某一类问题的算法是唯一的；②算法必须在有限步数后停止；③算法的每一步都必须清晰，不能有歧义或歧义 ④算法执行后，肯定会产生一定的结果。A, 1 B, 2 C, 3 D, 4 2. 在数学中，现代意义上的算法是指 () A. 用阿拉伯数字计算的过程 B. 解决某类问题的程序或步骤

C. 计算机以有限的步骤完成，用于解决某一类问题的清晰有效的程序或步骤 D. 用计算机进行数学运算的方法

3.你必须坐火车去另一个地方做紧急任务。请写下从你的房间开始到坐在马车上的三步主要算法S1、S2、S3。

4、任意给定一个正实数，设计一个算法，求以这个数为半径的圆的面积。5. 有蓝色和黑色两个墨水瓶，但是现在蓝色墨水错误地安装在黑色墨水瓶中，黑色墨水错误地安装在蓝色墨水瓶中。需要交换它们。请设计一个算法来解决这个问题。分析：由于两个墨水瓶中的墨水不能直接交换，可以考虑引入第三个空墨水瓶来交换。

6. 写一个算法，求直线包围的面积和两点的坐标轴M(-3,-1), N(2,5)). 参考答案

1. C 2. C 3. 坐车到火车站，买票，持票上车找座位。4. 第一步：输入任意一个正实数r；步骤 2：计算 S=πr；第三步：输出圆S.5的面积。解：算法步骤如下：

第一步：拿一个空墨水瓶，调成白色；第二步：将黑色墨水瓶中的蓝色墨水放入白色墨水瓶中；

2第三步：将蓝色墨水瓶中的黑色墨水倒入黑色墨水瓶中；第四步：将白瓶中的蓝墨水倒入蓝瓶中；第五步：结束交换。6. 解决方案： 算法：

第一步：取x1=-3，y1=-1，x2=2，y2=5；第二步：计算y-y1x-x1；＝y2－y1x2－x1 第三步：在第二步的结果中设置x=0，得到y的值m，得到直线与y轴的交点(0,m)；第四步：在第二步的结果中，设置y=0得到x的值n，得到直线与x轴的交点(n,0);第五步：计算S =1|m||n|; 第六步：输出运算结果。

高中数学1.1 算法教案的意义 6 苏教版必修3

高中数学《正弦定理》教案3苏教版必修5

高中数学1.1

1.1 高中数学收藏教案

必修高中数学3经典教案合集

高中数学1.1.1 算法概念教学计划2 新人教A版必修3

高中数学必修2教学设计：1.1.1 算法概念教学计划

高中数学必修3教学反思

高中数学《正弦定理》教案1苏教版必修5

高中数学1.2流程图选择结构教学计划江苏教育版必修3

教案网123