【每日一题】等腰三角形学生知识状况分析(一)

等腰三角形学生知识状态分析本节课是等腰三角形的第三课时通过中间两课时的学习教师已经把握了等腰三角形的相关性质并了解了用综合法证明命题的基本规定和方法为学习等腰三角形的判断公式确立了常识和技巧的基础2教学任务分析本节课的主要任务是构建等腰三角形的判断公式在复习性质定律的基础上鼓励学生反过来思考猜想新的命题并进行证明这种可以演进学生的反向思维能力同时引入反证法的基本证明模式学习与利用反证法也作为本课时的课堂任务之一所以本节课的课堂目标定为1.探索等腰三角形判定推论.2.理解等腰三角形的判断公式并会利用其进行简单的证明.3.了解反证法的基本证明模式并可简单应用4.培养学生的逆向思维能力3教学过程分析本节课的课堂过程设计了下面六个环节复习引入--逆向思考定理证明---巩固练习----适时提问导出反证法---拓展延伸----课堂小结第一环节复习引入活动过程通过问题串回顾等腰三角形的性质定律或者证明的模式规定学生独立构想后再进交流问题1等腰三角形性质定理的内容是哪个这个命题的题设和推论分别是哪个问题2我们是怎样证明上述定理的难题3我们把性质定律的条件跟结论反过来还建立么即使一个三角形有两个角相同那么这两个角所对的边也相同活动意图设计是问题串是为引出等腰三角形的判断公式埋下伏笔学生独立构想是对上节课内容有效地测试方法第二环节逆向思考定理证明活动过程与效果教师上面我们改变问题条件得出了众多类似的推论这是探究问题的



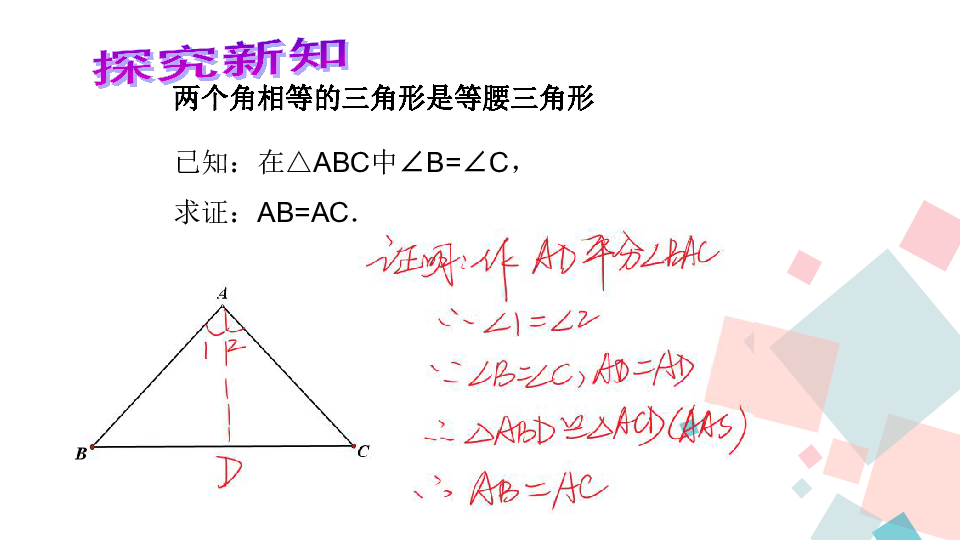
一种常用手段除此之外我们还可以ldquo反过来rdquo思考问题这只是获得数学推论的一条途径.例如ldquo等边对等角rdquo反过来成立吗也就是有两个角相同的三角形是直角三角形吗[生]如图在△ABC中angBangC要想证明ABAC只要构造两个全等的三角形使AB与AC成为对应边就可以了.[师]你是怎样想到的[生]由上面定理的证明取得启发包括作BC的中线或作A的平分线或作BC上的高都可以把△ABC分成两个全等的三角形.[师]很好.同学们可在练习本上尝试一下是否那么之后分组讨论.[生]我们组看到如果作BC的中线虽然把△ABC分成了两个三角形但能够用公理和已证明的定律证明他们全等.因为我们受到的条件是两个三角形对应两边以及一边的对角分别相同是不能够判断两个三角形全等的.后两种方式是可行的.[师]那么就请同学们任选一种方法按规定将推理证明过程书写下来.教师能使两个同学在黑板上演示并对推理证明过程讲评证明略[师]我们用ldquo反过来rdquo思考问题获得并证明了一个非常重要的反例mdashmdash等腰三角形的判断公式有两个角相同的三角形是直角三角形.这一定律可以简单描述为等角对等边.我们虽然看到了几何图形的对称美也看到了英语语言的对称美.第三环节巩固训练活动过程与效果将书中的课后训练提前到此是为了尽快巩固判定推论引导学生进行预测已知如图angCAE是△ABC的外角AD∥BC且ang1ang2.求证AB


AC.证明∵AD∥BCthere4ang1angB两直线垂直同位角相等ang2angC两直线垂直内错角相等.又∵ang1ang2there4angBangC.there4ABAC等角对等边.第四环节适时提问导出反证法活动过程与效果我们类比推论获得一个数学结论ldquo反过来rdquo思考问题也获得了一个数学推论.如果否定命题的条件能否也可获得一个数学结论吗我们一起来ldquo想一想rdquo小明说在一个三角形中即使两个角不相同那么这两个角所对的边也不相同.你觉得这个论断成立吗如果成立你可证明它吗有学生强调ldquo我觉得这个论断是成立的.因为我画了几个三角形观察并测量发现即使两个角不相同它们所对的边也不相同.但应像证明ldquo等角对等边rdquo那样却很难证明由于它的条件跟结论都能否定的.rdquo的确如此.像某些从正面人手很难证明的论断我们有没有别的证明模式跟技巧呢我们来看一位同学的看法如图在△ABC中已知angBneangC此时AB与Ac要么相同应么不相等.假设ABAC那么按照ldquo等边对等角rdquo定理可得angCangB但已知条件是angBneangC.ldquoangCangBrdquo与已知条件ldquoangBneangCrdquo相冲突因而ABneAC你可理解他的推理过程吗再比如我们应证明△ABC中不可能有两个直角也可以运用这位朋友的证法假设有两个角是直角不妨设angA90等腰三角形知识点及典型习题教案模板3


degangB90deg可得angAangB180deg但△ABangAangBangC180degldquoangAangB180degrdquo与ldquoangAangBangC180degrdquo相冲突因而△ABC中不可能有两个直角.引导学生探讨上一道面的证法有哪些共同的特征呢引出反证法都是先假定命题的推论不建立之后从而计算出了与已知或公理或未证明过的定律相冲突使得证明命题的推论一定建立.这只是证明命题的一种方法我们把它叫做反证法.接着用ldquo反过来rdquo思考问题的方式取得并证明了等腰三角形的判断公式ldquo等角对等边rdquo最后结合实例了解了反证法的涵义.第五环节拓展延伸活动过程与效果在一节课结束之际为培养学员思维的综合性灵活性特安排了2个练习一个是通过平行线角平分线判定三角形的图案再借助线段的转化求图形的周长另一个是一个开放性的难题考察学生多视角多维度思考问题的素养学生在独立构想的基础上再小组交流1如图BD平分angCBACD平分angACB且MN∥BC设AB12AC18求△AMN的边长2现有等腰三角形纸片如果可从一个角的顶点出发将原纸片一次剪开成两块等腰三角形纸片问此时的等边三角形的锐角的度数第六环节课堂小结1本节课学习了这些内容2等腰三角形的判断方式有那几种3结合本节课的学习谈谈等腰三角形性质跟判断的差别和联系.4举例谈谈用反证法说理的基本模式NMCBADPAGE等腰三角形知识点及典型习题教案模板3
和生产关系不大