2019年高中数学教资面试，你准备好了吗？

谢邀~

距离2019年下教资面试大约只有10天的时间啦~相信这些要考大学物理教资面试的小伙伴已经打算出来了，但是也有一部分小伙伴和题主一样，还在为究竟如何打算发愁，这不小7就来啦~我们一起聊一聊，如何在剩下的这段时间里快速备考高中数学教资面试。

一、制定具体的学习规划，严格执行

二、了解面试得分点，精准备面

三、10天快速备考攻略

一、制定具体的学习规划，严格执行。

首先，没有计划是不能打一场漂亮的胜仗的，所以想要在成功借助面试，肯定是必须先建立学习计划，因为时间迫切，所以需要准确到小时或者至分。具体的一天什么时候学习，学习多久可以按照自己的时间来建立。大致的计划可以参考下列：

首先，听理论课。了解考试内容是哪个，结构化是哪些，高中语文的基本课型，以及在不同课型的培训过程中需要怎样组织教学活动，这是前期练习的基础；

其次，消化吸收理论课的常识。可以自己画一个思维导图进行总结并标记训练重点，后面再练习时跟随思维导图走。例如下面：

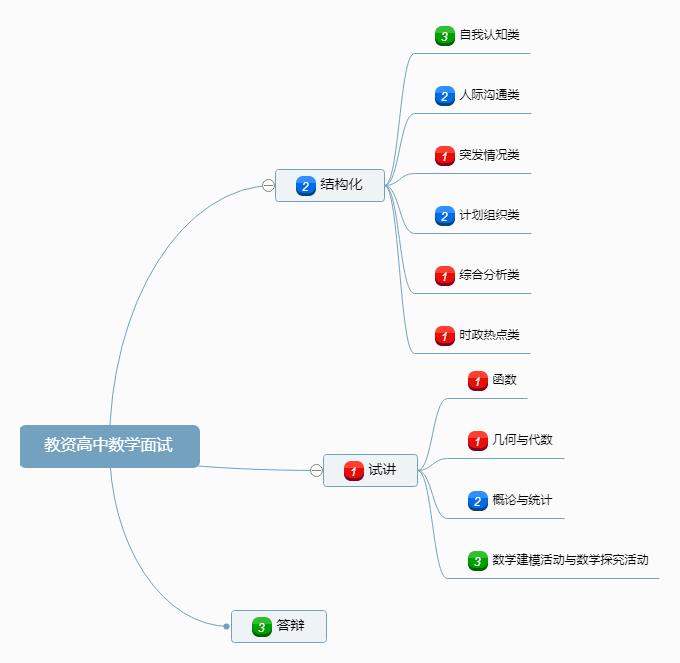
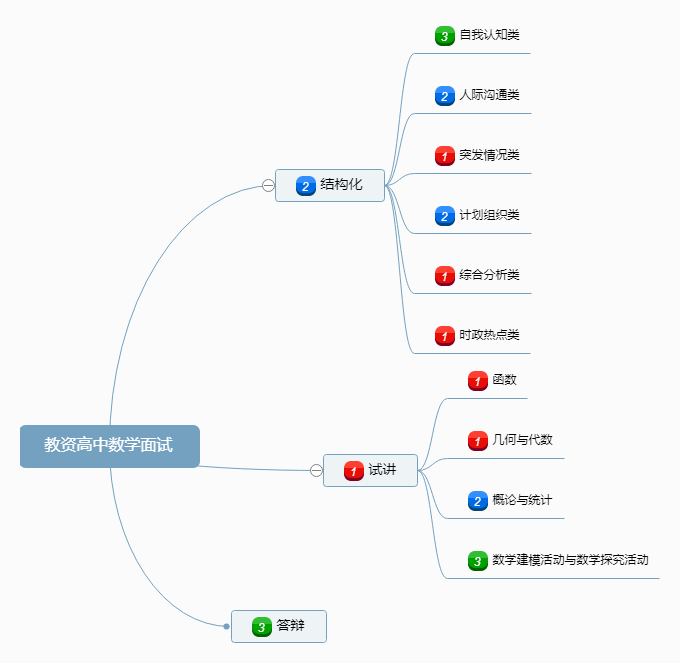
1代表更重要，2代表次重要，3代表不是特别重要。同时也可以看起来试讲的复习是现阶段最重要的事情。

最后就是每天不断的训练了。可以根据先部分再整体的方式进行练习，比如先训练导入、再练习新授，等等以此类推。

二、了解面试得分点，精准备面。

知己知彼才能百战不殆，所以知道面试的得分点是必不可少的环节。当然面试的得分点也有按照观众手中的评分方案来评分的，所以我们来说说评分细则到底长什么样吧~

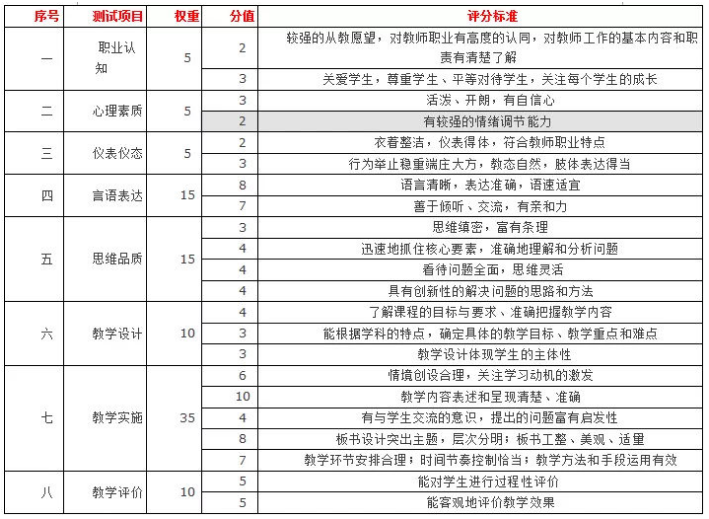
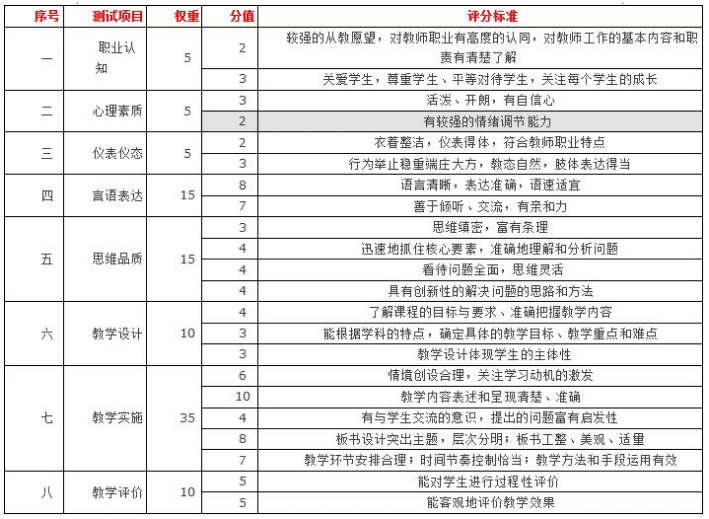
中学教资面试评分细则

所以依据评分政策来看，我们的试讲重点应当是语言表达应清晰流畅、要以学生为主体，与学生进行交流，要把握好教学的目标及重难点，教学环节，时间等应安排合理。做好这些相信面试肯定没有问题啦~

三、10天快速备考攻略

当然有的小伙伴看了以上可能还是不知道怎么样高效快速备考，那么小7现在帮正式上考场的小伙伴们一个速成锦囊，希望对大家预备教师有所帮助！

第1-2天：

了解高中数学教资面试理论常识。以下是需要应知道的理论常识

结构化：结构化题目一共有6类，分别为自我认知类题目、人际沟通类题目、突发状况类题目、计划组织类题目、综合预测类题目、时政热点类题目。

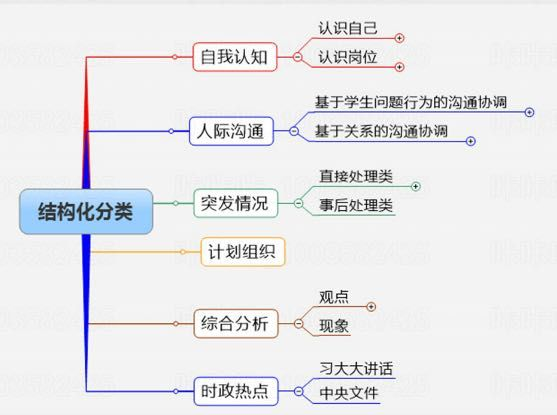
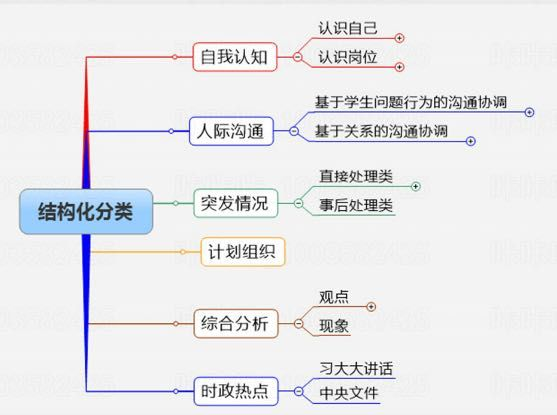
之所以应对他们进行分类，是因为不同同类型的考题答题策略不一样，至于怎样答题，请往下看：

01 自我认知类

考察人生历程、价值观、人生方向跟目标、兴趣爱好、优势跟劣势等内容。通常会问你最喜欢的人/事/物是哪个？你的优缺点是哪个？怎样变成优秀的老师等等。

答题套路：

从教师观、教师职业道德出发，表现出对岗位的热爱与奉献。

02 人际关系类

考察教师与师生、家长、同事、领导发生冲突时，怎样解决难题。

答题套路：

①调整心态：冷静、耐心、倾听；

②沟通了解：分析问题造成原因，并给出解决方案；

③防微杜渐：召开例会、组织活动、吸取教训。

03 突发情况类

考察老师对突发状况的缓解能力，提问方式如教学上/活动中/放学路上…突然出现…

答题套路：

①保持冷静，快速反应；

②课堂为重，以人为本；

③轻重缓急，有序处理；

④多方协调，合作完成。

04 计划组织类

考察老师组织一次活动、比赛、会议…的能力。

答题套路：

①组织活动的意义

②事前调研：听取父母/学生/同事意见；

③事中安排：确定步骤，安排人员工作，做好记录；

④事后反思：分享活动影像、照片，总结经验教训。

05 综合分析类

考察老师对某一社会现象、某一观点、某种行为的见解。

答题套路：

①点题，这个现象/观点的意思；

②合理之处；

③不合理之处；

④总结，作为老师怎样扬长避短。

07 时政热点类

考察对学生相关的政策理解。

答题套路：

①点题，解释意思；

②分析意义，对学生、对大学、对社会的影响；

③如何践行，你会怎么做；

④总结。

来说说具体实例

1.计划组织类：教室里最吵闹，作为班主任你走进去后该如何办？

2.自我认知类：教师应面对压力跟突发情况，你如何看？

3.综合预测类：学生收到压岁钱后铺张浪费，作为班主任的你会如何办？

4.突发状况类：课堂上两个同学突然打出来了，你如何处理？

5.人际沟通类：家长对你有看法，你该怎么面对？

7.时政热点类：教师应做学员的四个引路人，请你回答“四个引路人”是哪个？

试讲：

考试四大课型：函数、几何与数论、概率与统计、数学模型活动与数学研究活动。

函数高频考点

《单调性》

《偶函数》

《任意角的三角函数》

《三角函数的诱导公式》

几何与代数高频考点

《直线与平面垂直的判定》

《圆的一般方程》

《空间直角坐标系》

概率与统计高频考点

《抽签法》

《古典概型》

真题呈现：

圆的标准方程

古典概型

古典概型

教案基本框架

一、教学目标

1、知识与技能目标

2、过程与技巧目标

3、情感、态度、价值观目标

二、教学重点/难点

1.教学重点

2.教学难点

三、教学过程

1.导入新课

2.新课讲授

3.巩固加强

4.课堂小结

5.布置作业

五、板书设计

常见的数学思想：

1.函数与方程的思想

用数组和变量来探讨问题的方式就是函数思想,函数思想是变量概念、图象和性质等常识更高层次的提炼和概括,是在常识和技巧反复学习中写实出的具有意识的指导原则.

深刻理解变量的图像跟性质是应用变量思想解题的基础,运用方程思想解题可推论为三个步骤：①将所遭遇的难题转化为方程问题；②解这个方程或争论这个定理,得出相关的推论；③将所得出的推断再返回至原问题中去.

2．数形结合思想

在学校英语里,我们不可能把“数”和“形”完全孤立地割裂开,也就是说,代数问题可以几何化,几何难题也可以代数化,“数”和“形 ”在必定条件下可以互相转换、相互渗透.

3．分类讨论思想

在数学中,我们经常必须按照研究对象性质的差别.分各种不同情况给予考察,这是一种重要物理观念方法跟重要的解题思路 ,引起分类争论的诱因较多,归纳出来主要有下列几个方面：（1）由物理概念、性质、定理、公式的限制条件导致的讨论；（2）由数学变形所必须的限制条件所造成的分类讨论；（3）由于图形的不确定性引起的讨论；（4）由于题目含有字母而导致的讨论.

分类讨论的解题方法通常是：（1）确定讨论的对象或者被讨论对象的全体；（2）合理分类,统一标准,做到既无遗漏又无重复 ；（3）逐步讨论,分级进行；（4）归纳总结做出整个题目的论断.

4.等价转化思想

等价转换是指同一命题的等价方式.可以借助变量问题的条件跟结论,或借助适当的代换转换问题的方式,或借助互为逆否命题的等价关系来实现.

第3天：

练习写教学目标、教学重难点。

教学目标模板：

【知识与技能目标】理解XXX，掌握XX的概念，了解XXX，发现XXX。

【过程与技巧目标】 结合XXX，经历从详细的直观描述到形式的符号表达的具象过程，加深对

XXX的理解。

【情感态度与价值观目标】在XXX过程中，提升物理能力/直观想象和物理应用观念/运算素养/

逻辑推理素养。

示例展示：

知识与技能目标

理解并把握对数函数的概念，掌握对数函数的图像的初步画法。

过程与方式目标

发现并推论对数函数的性质，体会数形结合的观念方法。

情感态度与价值观目标

在参与函数图像的探讨过程中，提升物理能力跟化学应用观念。

教学重难点模板：

重点：

理解XXX，掌握XX的概念。（概念）

会求XXX

难点：

XXX的证明（定理）

XXX的计算过程（公式）

示例展示：

教学重点

对数函数的定义、图象。

教学难点

对数函数的底数对图象的影响。

第4天：

形成导入部分讲义模版、练习导入试讲（可先写试讲稿）

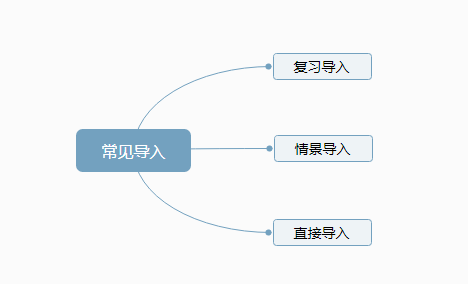
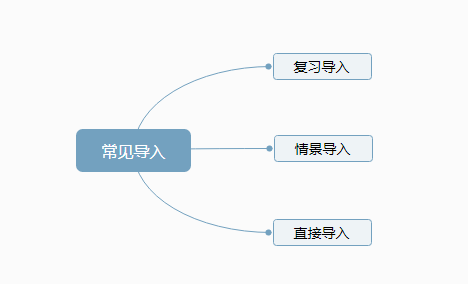
教案示范：

1、提出问题，导入新知

引例1：商场参加抽奖活动，顾客随意掷两颗骰子，如果点数之跟高于10，则会赢得精美奖品一份，问客人能得到奖品的概率是多少？

设计动机：带领学生复习古典概型的特征以及概率公式，为引发几何概型做好铺垫。

引例2：为了提高趣味性，商场又打算了两个转盘，甲乙双方玩转盘游戏，规定当指针指向B区域时，甲获胜，否则乙获胜，这两种状况下分别求甲获胜的几率是多少？

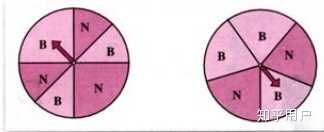
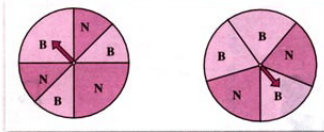
设计动机：以实际问题导致教师的学习兴趣跟求知欲望； 以此为铺垫，通过详细问题情境引入课题； 简单直观，符合学生的思维习惯跟认知规律。

试讲稿示范：

敬的诸位评委老师，大家晚上好，我抽到的试讲题目是《几何概型》，下面开始我的试讲。

同学们上课，同学们请坐，同学们请看大屏幕，这是某酒吧在国庆节开业当日的火爆场景，商场正在参加抽奖活动，顾客随意掷两颗骰子，如果点数之跟等于5，则会赢得精美奖品一份，问客人能得到奖品的概率是多少？同学们思考一下，老师请一位同学来提问，来，第三排穿黑色衣服的男朋友你来说，好，请坐，他说答案1/9，怎么得出这个结果的呢，对，有同学说运用古典概型概率公式推导得到的，同时掷两个骰子的结果共有36种，点数之跟等于5的状况有4种，因此按照公式推导可得

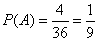
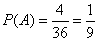
。这是我们上节课学习过的古典概型，看来大家都把握的非常好，继续看大屏幕，为了提高趣味性，商场又打算了两个转盘，甲乙双方玩转盘游戏，规定当指针指向B区域时，甲获胜，否则乙获胜，这两种状况下分别求甲获胜的几率是多少？

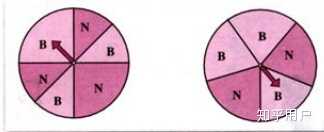
这个难题，大家反思一下如何来解决，还能不能用我们学过的常识计算出结果呢？

同学们观察这个转盘，求出甲获胜的几率貌似古典概型，但是鉴于这个难题中的基本事件必须是“指针指向的位置”，而不是“指针指向的区域”，因此就有无限多种可能，不满足有限性的特征，所以不能用古典概型解决难题，在特定状况下，我们可以用几何概型来推导试讲发生的概率，也就是我们最近要学习的内容。

第5-7天：

练习新授教案及试讲

教案示范：

2、师生合作，探究新知

提出问题后，第一，学生回顾古典概率公式：

其次，转盘（1）为游戏工具，甲获胜的概率为1/2，以转盘（2）为游戏工具时，甲获胜的概率为3/5；甲获胜的概率与字母B所在扇形区域的弧形的宽度有关，而与字母B所在区域的位置无关。

如果每个事件出现的概率只与组成该事件区域的宽度（面积或密度）成比例，则称这种的概率模型为几何概率模型。

因此，设图中转盘游戏中圆周的长度为1，则（1）中，

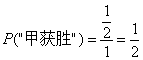
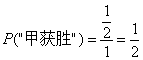
在（2）中，

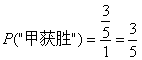
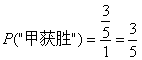
试讲稿示范：

继续来看这个转盘，整个转盘有六个区域高中数学试讲教案模板，B区域占了其中的三份，只要指针落在B区域，甲就获胜，这样（1）转盘中，甲获胜几率是不是就是3/6，也就是1/2，以转盘（2）为游戏工具时，同理，得到甲获胜的概率为3/5，这个例子表明了哪些问题呢？

两个转盘中字母B所在区域的方向、位置都有所变化，但是计算概率的之后有没有考虑位置的原因呢，对，没有，而事实上，甲获胜的几率与字母B所在扇形区域的弧形的宽度有关，而与字母B所在区域的位置无关，只要字母B所在扇形区域的弧形的宽度不变，不管这种区域是相邻，还是不相邻，甲获胜的几率是不变的。

如果每个事件出现的概率只与组成该事件区域的宽度（面积或密度）成比例，则称这种的概率模型为几何概率建模，简称几何概型。古典概型有推导定理，同样几何概型也有计算推导：

因此，设图中转盘游戏中圆周的重量为1，那么游戏中的几率就可以进行计算，老师请两位朋友分别在黑板中写出计算过程跟结果，其他同事自己在作业本上写成。都写到了吧，来看黑板上的答案，（1）中，

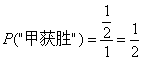
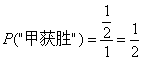
在（2）中，

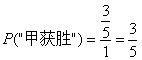
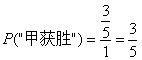
，跟他们计算的都一样吗，对，非常好！

第8天：

练习巩固小节、布置作业教案及试讲

巩固是对本课所学知识的一个回顾和巩固， 好的巩固方法可以帮助学员巩固所学知识，强化认识,

巩固环节主要使用练习法。可以是课后习题，也可以是自主设计题目。

巩固模板：

课堂小结模版：

本节课你学到了哪些知识?

用英语语言如何表述XX定理？

在XX定理的证明过程中主要利用了这些方式？

从该节课的学习活动中你收获了哪些方式？ 感悟到哪些数学观念方法?

你从本节课的语文学习学校到了哪些？

涉及到本节课重难点即可

常用的布置作业：

教案示范：

3、巩固练习，内化新知

例：某人午觉起床，发现表停了，他关掉收音机，想听电台报时，求他期待的时间不多于10分钟的概率。

4、课堂小结

这节课你有这些收获，学到了哪些？

5、布置作业

完成课后习题以及大屏幕上的作业题。

1．已知4路公交车每5min一班，在站台停1min，求乘客前往车站立即乘上车的概率.

2. 在1万平方千米的水域中有40平方千米的大陆架储藏着石油，假设在水域中任意一点钻探，钻至油井面的概率是多少？

试讲稿示范：

下面老师再考考大家，大屏幕中这个题目，一起来看一下，某人午觉起床，发现表停了，他关掉收音机，想听电台报时，求他期待的时间不多于10分钟的概率。他在一个小时内开启收音机的几率可能是一样的，但是这个时间里有无穷多个时间，显然用古典概型解决不了这个难题，那我们能否可以用几何概型公式推导呢，我们了解电台报时有频率的，所以他在那个时间段打开收音机的概率只与该时间段的长度有关，与时间段的位置无关，所以可以用几何概型来推导，设A集合是期待的时间不多于10分钟，事件A恰好是开启收音机的时刻位于[50,60]时间段内，因此用公式直接求解得到：

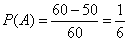
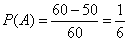
，也就是等待报时的时间不超过10分钟的概率为1/6。

好，这节课上到这时间终于差不多了，回顾一下这节课你学到了哪些？左边靠窗户那位女朋友你回答一下，恩，她说学会了古典概型的涵义及定理应用，对高中数学试讲教案模板，大家在推导的之后注意区别古典概型和几何概型的不同，试验的所有可能是无穷多的状况就考量几何概型，选用正确的定理解决难题是这节课的重点也有难点。

课后大家完成试卷以及大屏幕上的作业题。

1．已知4路公交车每5min一班，在站台停1min，求乘客前往车站立即乘上车的概率.

2. 在1万平方千米的水域中有40平方千米的大陆架储藏着石油，假设在水域中任意一点钻探，钻至油井面的概率是多少？

今天的课就先上到这，同学们，下课！

第9-10天：

全篇练习

通俗的说就是将上面几天练习的全部串起来啦~

练习小建议：

找上几个一同备考的小伙伴，彼此充当评委，练习结构化和试讲。没有小伙伴可以帮忙家人临时客串一下考官，如果是自己一个人，那就帮忙一下镜子君吧。有条件的最好在黑板上训练一下板书，不便于的也要在纸上写写画画，板书的整齐与否还是太妨碍考官评分的。

以上就是关于大学物理教资面试的复习干货啦~希望还能对大家小伙伴有所帮助~

最后，送各位阅读到此处的小可爱们一份礼物，希望在面试中助你一臂之力~

1、结构化：高频真题、万能套句、124个结构化问题

2、试讲：教案+试讲稿+音频、视频示范课

3、电子课本