【每日一题】集合A是集合B的子集

如果集合A的任何一个元素都是集合B的元素，我们说这两个集合有包括关系，称集合A是集合B的子集。一起看看高一语文必修一教案!欢迎查阅!

高一语文必修一教案1

教学目的：(1)了解集合之间的包括、相等关系的意义;

(2)理解子集、真子集的概念;

(3)能运用Venn图表达集合间的关系;

(4)了解与空集的意义。

教学重点：子集与空集的概念;用Venn图表达集合间的关系。 教学难点：弄清元素与子集 、属于与包括之间的区分;

教学过程：

四、 引入课题

1、 复习元素与集合的关系——属于与不属于的关系单一科目教案模板，填以下空白：(1)0 N;(2

;(3)-1.5 R

2、 类比实数的大小关系，如5

布课题)

五、 新课教学

A={1，2，3}，B={1，2，3，4}

集合A是集合B的部分元素组成的集合，我们说集合B包含集合A;

如果集合A的任何一个元素都是集合B的元素，我们说这两个集合有包括关系，称集合A是集合B的子集(subset)。

记作：A?B(或B?A)

读作：A包括于(is contained in)B，或B包含(contains)A (一) 集合与集合之间的“包含”关系;

当集合A不包括于集合B时，记作

B

用Venn图表示两个集合间的“包含”关系 A?B(或B?A)

(二) 集合与集合之间的 “相等”关系;

A?B且B?A，则A?B中的元素是一样的，因此A?B

结论：

任何一个集合是它原本的子集

(三) 真子集的概念

若集合A?B，存在元素x?B且x?A，则称集合A是集合B的真子集(proper subset)。

记作：A B(或B A)

读作：A真包含于B(或B真包含A)

(四) 空集的概念

(实例引入空集概念)

不带有任何元素的集合称为空集(empty set)，记作：? 规定： 空集是任何集合的子集，是任何非空集合的真子集。

(五) 结论：1A?A ○2A?B，且B?C，则A?C ○

(六) 例题

(1)写出集合{a，b}的所有的子集，并强调其中这些是它的真子集。

(2)化简集合A={x|x-3>2},B={x|x?5}，并表示A、B的关系;

(七) 归纳总结，强化思想

两个集合之间的基本关系只有“包含”与“相等”两种，可类比两个实数间的大小关系，同时需要切记区别“属于”与“包含”两种关系以及表示方式;

1 已知集合A?{x|a?x?5}，B?{x|x≥2}，且满足A?B，求实数a的○

取值范围。

2 设集合A?{○四边形}，B?{平行四边形}，C?{矩形}，

D?{正方形}，试用Venn图表示他们之间的关系。

高一语文必修一教案2

教学目的：(1)理解两个集合的并集与交集的的意义，会求两个简单集合的并集与交集;

(2)理解在给定集合中一个子集的补集的涵义，会求给定子集的补集;(3)能用Venn图表达集合的关系及运算，体会直观图示对理解抽象概念的作用。

课 型：新培训

教学重点：集合的交集与并集、补集的概念;

教学难点：集合的交集与并集、补集“是哪个”，“为什么”，“怎样做”;

教学过程：

六、 引入课题

我们两个实数除了可以非常大小外，还可以进行乘法运算，类比整数的乘法运算，两个集合是否也可以“相加”呢?

思考(P9思考题)，引入并集概念。

七、 新课教学

1. 并集

一般地，由所有属于集合A或属于集合B的元素所构成的集合，称为集合A与B的并集(Union)

记作：A∪B

Venn图表示： 读作：“A并B” 即：A∪B={x|x∈A，或x∈B}说明：两个集合求并集，结果还是一个集合，是由集合A与B的所有元素构成的集合(重复元素只看成一个元素)。

问题：在上图中我们不仅研究集合A与B的并集外，它们的公共部分(即问号部分)还应是我们所关心的，我们称其为集合A与B的交集。

2. 交集

一般地，由属于集合A且属于集合B的元素所构成的集合，叫做集合A与B的交集(intersection)。

记作：A∩B

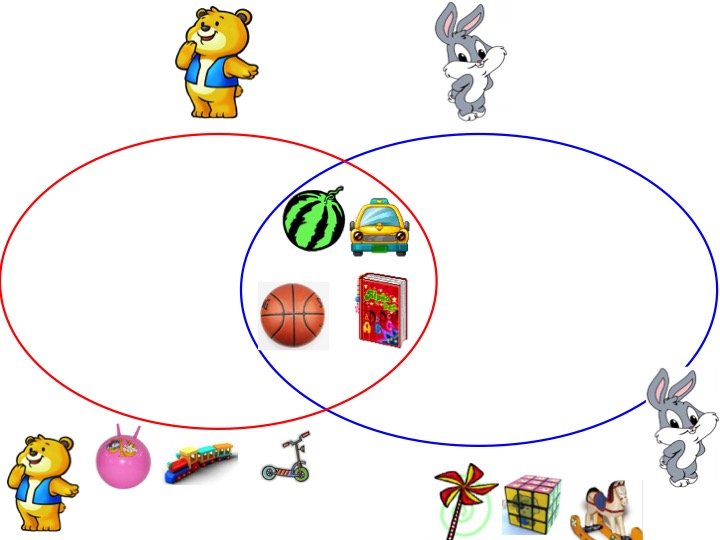
读作：“A交B” 即： A∩B={x|∈A，且x∈B}

交集的Venn图表示

说明：两个集合求交集，结果还是一个集合，是由集合A与B的公共元素构成的集合。 拓展：求以下各图中集合A与B的并集与交集

集

3. 补集

全集：一般地，如果一个集合带有我们所探究问题中所涉及的所有元素，那么就称这个集合为全集(Universe)，通常记作U。

A

说明：当两个集合没有公共元素时，两个集合的交集是空集，而不能说两个集合没有交补集：对于全集U的一个子集A，由全集U中所有不属于集合A的所有元素构成的集合称为集合A相对于全集U的补集(complementaryset),简称为集合A的补集，

记作：CUA

即：CUA={x|x∈U且x∈A}

补集的Venn图表示

说明：补集的概念需要应有全集的限制

4. 求集合的并、交、补是集合间的基本运算，运算结果依然还是集合，区分交集与并集的

关键是“且”与“或”，在处理有关交集与并集的问题时，常常从这两个字眼出发去探寻、挖掘题设条件，结合Venn图或数轴进而用集合语言表达，增强数形结合的观念方法。

5. 集合基本运算的一些推断：

A∩B?A，A∩B?B，A∩A=A，A∩?=?,A∩B=B∩A

A?A∪B，B?A∪B，A∪A=A，A∪?=A,A∪B=B∪A

(CUA)∪A=U单一科目教案模板，(CUA)∩A=?

若A∩B=A，则A?B，反之也成立

若A∪B=B，则A?B，反之也成立

若x∈(A∩B)，则x∈A且x∈B

若x∈(A∪B)，则x∈A，或x∈B

6. 课堂练习

(1)设A={奇数}、B={偶数}，则A∩Z=A，B∩Z=B，A∩B=?

(2)设A={奇数}、B={偶数}，则A∪Z=Z，B∪Z=Z，A∪B=Z

(3)集合A?{n|nm?1?Z}，B?{m|?Z}，则A?B?__________22

那么A?B?C?_______________,A?B?C?_____________;

八、 作业布置：(1) 已知X={x|x2+px+q=0，p2-4q>0},A={1,3,5,7,9},B={1,4,7,10}，且

(2) 集合A={x|x2+px-2=0},B={x|x2-x+q=0},若A?B={-2，0，1}，求p、q;

(3) A={2，3，a2+4a+2}，B={0，7，a2+4a-2，2-a}，且A?B ={3，7}，求B

高一语文必修一教案3

教材分析：函数是叙述客观世界变迁规律的重要物理建模.高中阶段虽然把函数看成变量之

间的依赖关系，同时还用集合与对应的语言描绘函数，高中阶段最强调函数模型化

的思想.

教学目的：(1)通过丰富实例，进一步体会函数是叙述变量之间的依赖关系的重要数学建模，

在此基础上学习用集合与对应的语言来描绘函数，体会对应关系在塑造函数概念中

的作用;

(2)了解构成变量的要素;

(3)会求一些简单方程的定义域和函数;

(4)能够恰当使用“区间”的符号表示这些变量的定义域;

教学重点：理解变量的模型化思想，用合与对应的语言来描绘函数;教学难点：符号“y=f(x)”的意义，函数定义域和函数的区间表示;

教学过程：

九、 引入课题

1. 复习高中所学函数的概念，强调函数的模型化思想;

2. 阅读教材引例，体会函数是叙述客观事物变化规律的物理建模的观念：

(1)炮弹的射高与时间的差异关系问题;

(2)南极臭氧空洞面积与时间的差异关系问题;

(3)“八五”计划以来我国城镇居民的恩格尔系数与时间的差异关系问题

备用实例：

我国2003年4月份非典疫情统计：

3. 引导学生应用集合与对应的语言表述各个例子中两个变量间的依赖关系;

4. 根据大学所学函数的概念，判断各个例子中的两个变量间的关系能否是函数关系.

高一语文选修一教案相关文章：

★ 人教版高一数学必修一教案模板

★ 关于高中必修1数学教案优秀范文合集大全

★ 人教版高一数学教案模板

★ 上海高一数学教案模板

★ 人教版高一数学必修一难点总结5篇

★ 最新精选高一语文选修1知识点归纳总结三篇

★ 高一高二英语必修1知识点整理

★ 高一语文必修一知识点必背难点总结5篇

★ 人教版高一数学必修一知识点归纳最新五篇

★ 高一语文必修一知识点梳理5篇最新