中小学1对1课外辅导专家龙文教育学科老师个性化教学案

中小学 1 对 1 课外辅导专家龙文教育学科教授个性化教学案教师 学科 类型 知识讲解□： 学生姓名 年级 考题讲解□: 上课日期 教材版本 本人课时统计 本月第（ 本年度共（ ）课时 ）课时教学案主 题课时数量三角形（全程或详细时间） 全程或具体时间）授课时段教学目标掌握三角形有关的直线、与三角形有关的角、多边形以及内角和 1、掌握三角形的基本概念，分类方式； 2、理解并把握三角形三边的内在关系； 3、掌握三角形中的主要线段——三角形的角平分线、中线和高； 4、三角形的内角和公式以及结论；多边形的锐角和及五边形的顶角和。 1、三角形三边关系的应用； 2、三角形中的主要线段——三角形的角平分线、中线和高； 3、三角形的锐角和公式以及结论 学生构建求知增智活动 教师鼓励启发过程教学重点、 教学重点、 难点考点分析 教学过程1中小学 1 对 1 课外辅导专家与三角形有关的直线 (1)三角形的定义 由不在同一直线上的三条线段首尾顺次相接所构成的图形叫做三 角形. 角形. (2)三角形的分类 C?不等边三角形 ? 三角形 ? ?底跟腰不相同的三角形 ① ( 按边 ) ?等腰三角形 ? ?等边三角形 ?a? 直角三角形 ? 三角形 ? ? 锐角三角形 ② 按角 ? 斜三角形 ? 钝角三角形 ? ?(3)三角形的主要线段 ①三角形的中线:顶点与对边中点的连线,三中线交点叫重心 ②三角形的角平分线:内角平分线与对边相交,顶点和端点间的 线段,三角角平分线的端点叫内心 ③三角形的高:顶点向对边作垂线,顶点和垂足间的直线.三条高的 交点叫垂心(分锐角三角形,钝角三角形和等腰三角形的端点的位 置不同)注：三条角平分线，三条中线都在三角形的外部，而三条高的位置与三 角形的图案有关：锐角三角形的三条高都在三角形内部；直角三角形的两条 直角边就是它的两条高，另一条高在三角形内部；钝角三角形的两条高在三 角形的内部，另一条高在三角形内部。

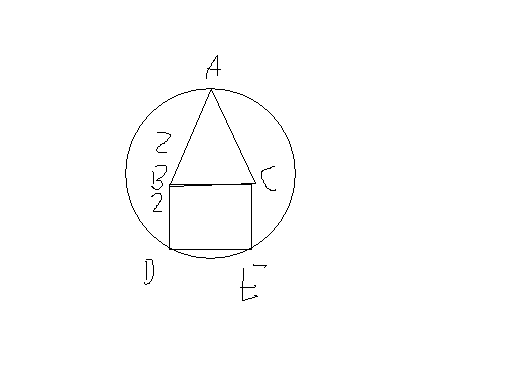
(4)三角形三边间的关系. ①两边之跟大于第三边 ②两边之差大于第三边 (5)三角形的稳定性: 三角形的三条边确定后,三角形的颜色跟大小不变了,这个性 质也称三角形的稳定性 例 1:已知 BD,CE 是 ?ABC 的高，直线 BD,CE 相交，所成的角中有一 个角为 50°， 则 ∠BAC等于2a + b > c, b + c > a , c + a > bc ? a

凹五边形 ③多边形的对角线的条数: A.从 n 边形的一个顶点可以引（n-3）条对角线，将多边形 分成（n-2）个三角形。 n(n ? 3) 条对角线。 B.n 边形共有 2 （4）多边形的顶角和公式及外角和 ①多边形的内角和等于（n-2）×180°(n≥3)。 ②多边形的锐角和等于 360°。 （5）平面镶嵌及平面镶嵌的条件。 ①平面镶嵌：用颜色相似或不同的图形封闭平面，把平面的 一部分既无缝隙，又不重叠地全部覆盖。 ②平面镶嵌的条件：有公共顶点、公共边；在一个顶点处各 多边形的锐角和为 360°。3中小学 1 对 1 课外辅导专家 三角形有关的角、 三角形有关的角、多边形以及内角1. 三角形的内角 1.如果三角形的三个内角的度数比是 2:3:4,则它是( ) A.锐角三角形 角形 B.钝角三角形; C.直角三角形 D.钝角或直角三2.下列表述正确的是( ) A.三角形的钝角中最多有一个锐角; C.三角形的锐角中最多有一个直角; B.三角形的钝角中最多有两个锐角 D.三角形的锐角都小于 60°3.已知三角形的一个内角是另一个内角的 角的度数分别为( ) A.60°,90°,75° C.48°,32°,38° B.48°,72°,60° D.40°,50°,90°,是第三个内角的,则这个三角形各内4.已知△ABC 中,∠A=2(∠B+∠C),则∠A 的度数为( ) A.100° B.120° C.140° D.160°5.已知三角形两个内角的差等于第三个内角,则它是( ) A.锐角三角形 B.钝角三角形 C.直角三角形 D.等边三角形6.设 α,β,γ 是某三角形的三个内角,则 α+β,β+γ,α+γ 中 ( ) A.有两个锐角、一个钝角 C.至少有两个钝角 B.有两个钝角、一个锐角 D.三个都可能是锐角7.在△ABC 中,∠A= A.锐角三角形∠B=∠C,则此三角形是( ) C.钝角三角形 D.等腰三角形B.直角三角形2。

三角形的外角 1.若一个三角形的一个外角小于与它相邻的内角,则这个三角形是( ) A.直角三角形 B.锐角三角形 C.钝角三角形 D.无法确认2.如果三角形的一个外角和与它不相邻的两个内角的跟为 180°,那么与这个锐角相邻 的外角的度数 为( ) A.30° B.60° C.90° D.120°3.已知三角形的三个外角的度数比为 2:3:4,则它的最大内角的度数为( ) A.90° B.110° C.100° D.120°4中小学 1 对 1 课外辅导专家4.已知直角三角形的一个外角是 120°,则它是( ) A.等腰直角三角形; 腰钝角三角形 B.一般的等腰三角形; C.等边三角形; D.等5.如图 1 所示,若∠A=32°,∠B=45°,∠C=38°,则∠DFE 等于( ) A.120° B.115° C.110° D.105°(1)(2)6.如图 2 所示,在△ABC 中,E,F 分别在 AB,AC 上,则以下各种不能成立的是( ) A.∠BOC=∠2+∠6+∠A; ∠1=∠ABC+∠4 B.∠2=∠5-∠A; C.∠5=∠1+∠4; D..3 多边形以及内角和 1.一个多边形的锐角中,钝角的个数不可能是( ) A.1 个 B.2 个 C.3 个 D.4 个2.不能作为正五边形的锐角的度数的是( )A.120°B.(128)°C.144°D.145°3.若一个多边形的各内角都相同,则一个内角与一个外角的度数之比不可能是( ) A.2:1 B.1:1 C.5:2 D.5:44.一个多边形的钝角中,锐角的个数最多有( ) A.3 个 B.4 个 C.5 个 D.6 个5.四边形中,如果有一组对角都是直角,那么另一组对角可能( ) A.都是钝角; C.是一个锐角、一个钝角 B.都是锐角 D.是一个锐角、一个直角5中小学 1 对 1 课外辅导专家6.若从一个多边形的一个顶点出发,最多可以引 10 条对角线,则它是( ) A.十三边形 B.十二边形 C.十一边形 D.十边形7.若一个多边形共有十四条对角线,则它是( ) A.六边形 B.七边形 C.八边形 D.九边形8.若一个多边形除了一个内角外,其余各内角之和为 2570°,则这个内角的度数为( ) A.90° B.105° C.130° D.120°.4 课题学习 镶嵌 1.用颜色、大小完全相等的图形不能镶嵌成平面形状的是( ) A.等腰三角形 B.正方形 C.正四面体 D.正多边形 2.下列图形中,能镶嵌成平面形状的是( ) A.正五边形 B.正七边形 C.正八边形 3.不能镶嵌成平面形状的正多边形组合为( ) A.正八边形和正方形 B.正五边形和正十边形 C.正多边形和正三角形 D.正多边形和正八边形 4.用正三角形和正十二边形镶嵌,可能情况有( ) A.1 种 B.2 种 C.3 种 C.4 种 5.用正三角形和正多边形镶嵌,若每一个顶点周围有 m 个正三角形、n 个正六边形,则 m,n 满足的关系式 是( ) A.2m+3n=12 B.m+n=8 C.2m+n=6 D.m+2n=6 D.正九边形例 1. 如图，已知 （A）， （B） （C） （D）（）6中小学 1 对 1 课外辅导专家例 2. 如图，在△ABC 的边 BC 上取两点 D、E，使 BD=CE，请你运用三角 形三边的关系跟平移的知识，观察 AB+AC 与 AD+AE 之间的长度关系，提出 一个设想，并加以证明.例 3. 如图（1）所示，△中， .的平分线交于点，求证：（1） （2） 变式 1：如图（2）所示等腰三角形知识点及典型习题教案模板3，△ 中，内角 分线交于点 ， . 中，外角（3） 和外角的平求证：变式 2：如图（3）所示，△ 于点 ， .的平分线交求证：7中小学 1 对 1 课外辅导专家 例 4. 如图，已知直角三角形的边长为 21cm，一腿上的中线把直角三角形 分成面积之差为 3cm 的两个三角形，求等腰三角形各边的长。

例 5. 已知：如图，在△ 别是边 上的高，中， 相交于 ，求，的度数。分例 6. 多边形的锐角和与某一个外角的度数总和为 数。等腰三角形知识点及典型习题教案模板3，求多边形的边8中小学 1 对 1 课外辅导专家 教师活动题目似乎简 单，也要 仔细呦！教学过程课堂练习课后作业 本节课课堂计划完成状况按时完成□ 提前完成□ 延后完成□ ____________________________ 学生的接受程度： 5 4 3 2 1 ______________________________学 生 成 长 记 录学生的教学表现：很积极□ 比较积极□ 一般积极□ 学生今天作业完成情况： 优□不积极□___________________________良□ 中□ 差□ 存在问题 _____________________________学管师（ 班主任） 学管师 班主任）_______________________________________________________________老 师 寄 语班主任教学教授9