各种性质、定理

在这里记录一下做题中遇到的各种性质、定理,数论知识偏多,没有什么顺序,只是做到了就记录一下,不断更新。。
④a与b的积除以c的余数等于a除以c的余数与b除以c的余数的积除以c的余数。一,公元年除以天干(10)的余数减3,即为天干.(若余数小于0或等于0,则加天干位10)。③a与b的和除以c的余数等于a除以c的余数加上b除以c的余数的和除以c的余数。
欧拉定理,(也称费马-欧拉定理)是一个关于同余的性质。欧拉定理表明,若n,a为正整数,且n,a互质,则:

欧拉函数
定义:用于计算 p(n),比n小的所有与n互质的数。
计算公式:p(n)=n*(1-1/p1)*(1-1/p2)....*(1-1/pk)【p1,p2,pk都是n的素因子】
另:若n=p1^q1*p2^q2*.....*pk^qk
则,p(n)=(p1-1)*p1^(q1-1)*(p1-1)*p2^(q2-1)......*(pk-1)*pk^(qk-1)
性质:若m,n互质,φ(mn)=φ(m)φ(n)。当n为奇数时,φ(2n)=φ(n)
欧拉定理:

a,m互质,a^φ(m)≡1(mod m)
例:2,3互质,那么,2^2%3=1
推论:对于互质的数a、n,满足a^(φ(n)+1) ≡ a (mod n)
欧拉公式的延伸:小于n 与n互质的数的和 是euler(n)*n/2
多个数的最小公倍数 每个数分解因子 质因子最高次幂相乘之积
质数就是在所有比1大的整数中,除了1和它本身以外,不再有别的约数,这种整数叫做质数或素数。质数:就是在所有比1大的整数中,除了1和它本身以外,不再有别的约数,这种整数叫做质数,质数又叫做素数。至于第几个出队的人糖果最多就是求1...n中约数最多的数 可以利用反素数相关知识。
性质一:一个反素数的质因子必然是从2开始连续的质数.
性质二:p=2^t1*3^t2*5^t3*7^t4.....必然t1>=t2>=t3>=....
约瑟夫: f[1] = 0; f[i] = (f[i-1]+m)%i;
高次幂取模:a^b%c = a ^(b%eular(c)+eular(c)) % c。 eular(c)为欧拉函数
鸽巢原理 :若有n个笼子和n+1只鸽子,所有的鸽子都被关在鸽笼里,那么至少有一个笼子有至少2只鸽子。

若有n个笼子和kn+1只鸽子,所有的鸽子都被关在鸽笼里,那么至少有一个笼子有至少k+1只鸽子。
推广定理拉姆齐(Ramsey)定理:又称拉姆齐二染色定理,是要解决以下的问题:要找这样一个最小的数n,使得n个人中必定有k个人相识或l个人互不相识。
Pick定理是说,在一个平面直角坐标系内,如果一个多边形的顶点全都在格点上,那么这个图形的面积恰好就等于边界上经过的格点数的一半加上内部所含格点数再减一。
pick定理的一些应用
内切圆半径
直角三角形中
1、两直角边相加的和减去斜边后除以2,得数是内切圆的半径:
r=(a+b-c)/2(注:s是Rt△的面积,a, b是Rt△的2个直角边,c是斜边)
2、两直角边乘积除以直角三角形周长,得数是内切圆的半径:
r=ab/ (a+b+c)
1)对于一般的三角形,内切圆半径公式如下:
[(s-a)(s-b)(s-c)/s]^(1/2)
s=(a+b+c)/2
R= abc/(4S)
= ¼ abc/√[p(p-a)(p-b)(p-c)]
=abc/√[(a+b+c)(-a+b+c)(a-b+c)(a+b-c)]
return earthradius * math.acos((math.sin(y1) * math.sin(y2) + math.cos(y1) * math.cos(y2) * math.cos(x2 - x1)))。y1=sin*cos*x2�sin*sin*y2�cos*z2- d*sin。e eedx x e x d x x x1 11) cos(ln 1 sin ) sin(ln ) sin(ln = =&minus。
x1,y1是纬度\经度的弧度单位,r为地球半径
已知任意四面体(三棱锥)六条棱的棱长,求其体积。
先取上底面的面对角线,计算,得到,根号2倍棱长 这根面对角线和它相交的棱,就是垂直于上底面的棱,又可以组成一个直角三角形,而这个直角三角形的斜边就是体对角线,根据勾股定理,得到,体对角线=根号3倍棱长.正方体属于棱柱的一种,棱柱的体积公式同样适用 (要正确区分体对角线和面对角线,面对角线是平面几何中的概念而体对角线是立体几何中的概念) 也可以用正方体的体积=底面积×高计算。(6)做题技巧:看题目所求的单位名称,平方一般是求表面积、侧面积或底面积,立方、l、 ml一般是求体积(容积),其他一般是求棱长或棱长和。14.表面积扩大棱长倍数的平方倍,体积扩大棱长倍数的立方倍。
V=
sqrt[ad(b+c+e+f-a-d)+be(a+c+d+f-b-e)+cf(a+b+d+e-c-f)-abf-bcd-cae-def)]/12

几何中的欧拉定理
设R为三角形外接圆半径,r为内切圆半径,d为外心到内心的距离,则:
d^2=R^2-2Rr
设v为顶点数,e为棱数,f是面数,则
v-e+f=2-2p
p为欧拉示性数,例如
p=0 的多面体叫第零类多面体
p=1 的多面体叫第一类多面体
连通图:
设一个二维几何图形的顶点数为V,划分区域数为Ar三角形欧拉定理,一笔画笔数为B,则有:
V+Ar-B=1
(如:矩形加上两条对角线所组成的图形,V=5,Ar=4,B=8)定理内容
( 欧拉公式的推广形式 ) 对于具有k(k≥ 1) 个连通分支的平面图G三角形欧拉定理,有n – m + r=k+1 。
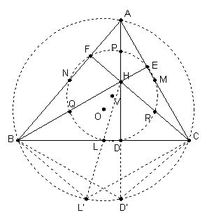
在同一个三角形中,它的外心Circumcenter、重心Gravity、九点圆圆心Nine-point-center、垂心Orthocenter共线。
记住