控制系统时域与频域性能指标的联系

控制系统时域与频域性能指标的联系

角． (1)给角求值的关键是正确地选用公式，以便把非特殊角的三角函 数相约或相消，从而化为特殊角的三角函数． (2)给值求值的关键是找出已知式与待求式之间的联系及函数的差 异，一般可以适当变换已知式，求得另外函数式的值，以备应用，同时 也要注意变换待求式，便于将已知式求得的函数值代入，从而达到解题。窗函数法设计fir滤波器的基本步骤(1) 根据技术要求确定待求滤波器的单位取样响应如果已知待求滤波器的频响：hd(ejw)，则：如果已知通带和阻带衰减和边界频率的要求，可选用理想滤波器作为逼近函数：hd(ejw) —〉 idft —〉hd(n)==〉(2) 根据过渡带及阻带衰减要求，确定窗函数及其长度设过渡带宽为：((，其值近似于窗函数主瓣宽度。} e可以更容易理解位移的连续性) 2. 收敛准则的数学描述 (1) 完备性： 若泛函中场函数的最高阶导数为m阶， 则场函数的试探函数至少应该是m次完全多项式， 即包含零阶至m阶导数为常数的项。

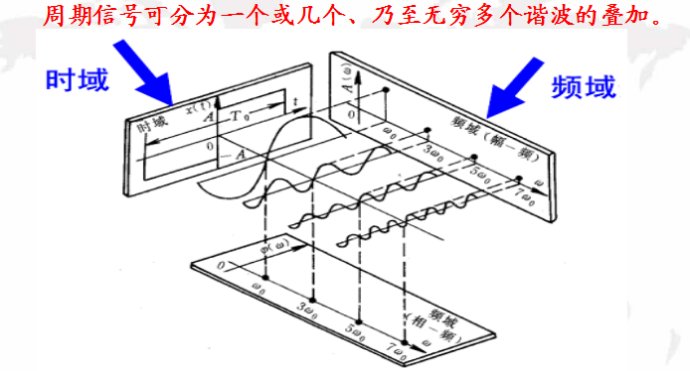
如果系统的开环传递函数未知，或者系统的阶次较高，就需采用频域分析法。频域分析法不仅是一种通过开环传递函数研究系统闭环传递函数性能的分析方法，而且当系统的数学模型未知时，还可以通过实验的方法建立。此外，大量丰富的图形方法使得频域分析法分析高阶系统时，分析的复杂性并不随阶次的增加而显著增加。

光知道如何选择配件是不行的，还要知道怎么选择合适宝贝的背景，具体的教程，请查看：简易背景的选用方法 复杂背景的选用方法。对于刚刚接触金融的同学来说，也许数学是个难题，不过这本书则通过详实的案例来为大家分析博弈论的实际用法。面对新的数学知识时，能主动地寻找其实际背景，并探索其应用价值．“方程（组）与不等式（组）”、“函数”所涉及到的内容，为实现上述“实际应用”提供了很数学工具，也正因为如此，借助于这样的工具系统时域和频域分析方法的关系系统时域和频域分析方法的关系，我们就可以将实际问题“模型化”了．事实上，在“数与代数”学习领域，充满了用来表达各种数学规律的模型，如代数式、方程、函数、不等式等．例如，结合实际问题，讨论绳长短问题（例15）、铁丝总长问题（例17）或调运量问题（例18）等，需要分析实际问题中的数量关系，建立和利用方程（组）或不等式（组）模型。

系统的时域性能指标与频域性能指标有着很大的关系，研究其内在联系在工程中有着很大的意义。

一、系统的时域性能指标

延迟时间

t d 阶跃响应第一次达到终值h (∞)的50%所需的时间 上升时间t

r 阶跃响应从终值的10%上升到终值的90%所需的时间；对有振荡的系统，也可定义为从0到第一次达到终值所需的时间 峰值时间

t p 阶跃响应越过终值h (∞)达到第一个峰值所需的时间 调节时间t s

断料时应避免用短尺量长料，防止在量料中产生累计误差。 b.断料时应避免用短尺量长料，防止在量料中产生累计误差。② 断料应避免用短尺量长料，以防止在量料中产生累计误差。

%σ=

()()()∞∞-h h h t p ⨯100%

二、系统频率特性的性能指标

881信号与系统(b)"""确定信号的特性、线性时不变系统的性质、信号通过线性系统的响应，以及连续和离散的信号与系统的复频域分析方法（包括傅里叶变换，拉普拉斯变换和z变换）。 传统形式的 gibbs 模型多以空间灰度信息的线性干涉关系为描述基础,由于实际图像中空间灰度信息的非线性关系,这类模型在诸如多纹理分割这样的应用中,有较大的局限性。文[]分析、 提出、 总结了pid控制器的设计方法，给出pid控制器在时域、 频域的设计步骤及性能评价指标等. 文[, ]最早提出了经典的ziegler-nichols(z-n)和cohen-coon(c-c) pid控制器调节方法，通过应用继电器产生周期性振荡来整定控制器. 基于描述函数方法，文[]提出了含有死区饱和的非线性系统pid控制器设计方法. 文[]提出了混合h2/h∞性能的鲁棒最优pid控制器设计方法. 文[]提出了基于双线性不等式优化的多变量最优pid控制器设计方法. 基于忆阻神经网络，文[]提出了一种pid控制器设计方法. 文[]采用标准线性矩阵不等式方法设计多变量h∞鲁棒最优pid控制器. 文[]采用多目标优化绝对误差积分性能指标，获得低阶被控过程最优pid控制器. 基于参数最优化方法、 新区间多项式稳定准则，文[, , , , , ]提出了最小方差pid控制器、 鲁棒最优pid控制器及带动态性能约束与ε-routh稳定性约束的最优pid控制器.。