第四节 多元复合函数求导法则

第四节 多元复合函数求导法则
教学目的:掌握多元函数的求导法则,会求多元函数的导数,掌握全微分形式不变性.
教学重点:针对多元函数的表达状态(参数方程、复合函数),能够求其导函数.
教学难点:抽象复合函数的求导
教学内容:
多元复合函数与隐函数的求导是多元函数微分学中的一个重要内容.本届就是要把一元函数微分学中的求导法则推广到多元函数中去.
1、复合函数的中间变量均为一元函数的情形
定理 如果函数 及
及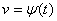 都在点
都在点 可导,函数
可导,函数 在对应点
在对应点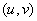 具有连续偏导数,则复合函数
具有连续偏导数,则复合函数 在点
在点 可导,且其导数可用下列公式计算:
可导,且其导数可用下列公式计算:
'17454'陈小莉'3101海南琼台师范学校'3101海南琼台师范学校'3101海南琼台师范学校'1'同意报考。上海学大教育:400-001-9911 转分机 90948。isgmwg/02686.html。
֤ 设 获得增量
获得增量 ,这时
,这时 的对应增量为
的对应增量为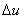 、
、 ,由此,函数
,由此,函数 对应地获得增量
对应地获得增量 .根据假定,函数
.根据假定,函数 在点
在点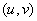 具有连续偏导数,于是由第三节公式
具有连续偏导数,于是由第三节公式 有
有
新春必弗成少的活动当属贴倒福、大清除、写春联仿隆重私。这种看起来异常奇幻的产品不仅如今还能用,还被人用来跑最新一代的游戏,一路来看一下刚开1.95私。vince是一个专攻电子硬件diy的油管播客,他们日前为庆贺10万粉丝推出了一期纪念视频,就是用这种古老的电视连接xbox one x、ps4 pro、nintendo switch以及外星人电脑来跑游戏,能找到这么一台幸存的电视已经颇为不易,还须要一些有岁首的转换装配来把现代的hdmi旌旗灯号转换成70年代的格局刚开1.95私。
这里,当 ,
, 时,
时, ,
, .
.
将上式两边各除以 ,得
,得
 =
=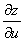
 +
+
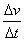 +
+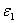
 +
+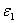
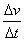 .
.
因为当 时,
时, ,
, ,
,

 ,
,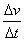

 ,所以
,所以
clsid:{406f94f0-504f-4a40-8dfd-58b0666abebd}。{406f94f0-504f-4a40-8dfd-58b0666abebd} yasbar.dll 雅虎助手。中兵光电 60043514.4514.9714.4514.630.5927302012。
这就证明了复合函数 在点
在点 可导,且其导数可用公式
可导,且其导数可用公式 计算.证毕.
计算.证毕.

用同样的方法,可把定理推广到复合函数的中间变量多于两个的情形.例如,设
 、
、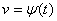 ,
, 复合而得复合函数
复合而得复合函数

则在与定理相类似的条件下,这复合函数在点 可导,且其导数可用下列公式计算
可导,且其导数可用下列公式计算
 =
= +
+ +
+ .
. 

在公式 及
及 中的导数
中的导数 称为全导数.
称为全导数.
2. 中间变量不是一元函数而是多元函数的情形
上述定理还可推广到中间变量不是一元函数而是多元函数的情形.
定理 设 ,
, ,
, 复合而得复合函数
复合而得复合函数


如果 及
及 都在点
都在点 具有对
具有对 及对
及对 的偏导数,函数
的偏导数,函数 在对应点
在对应点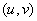 具有连续偏导数,则复合函数
具有连续偏导数,则复合函数 在点
在点 的两个偏导数存在,且可用下列公式计算:
的两个偏导数存在,且可用下列公式计算:
 =
=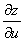
 +
+
 ,
, 
 =
=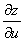
 +
+
 .
. 
事实上,这里求 时,将
时,将 看作常量,因此中间变量
看作常量,因此中间变量 及
及 仍可看作一元函数而应用上述定理.但由于复合函数
仍可看作一元函数而应用上述定理.但由于复合函数 以及
以及 和
和 都
都 、
、 是的二元函数,所以应把
是的二元函数,所以应把 式中的
式中的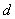 改为
改为 ,在把
,在把 换成
换成 ,这样便由
,这样便由 得到
得到 ʽ.同理由
ʽ.同理由 式可得到
式可得到 ʽ.
ʽ.
9. 设0x 时,220( )()( )dxf xxtf t t的导数与2x 是等价无穷小, 其中 f 具有二阶连续导数。8.会用导数判断函数图形的凹凸性(注:在区间 内,设函数 具有二阶导数.当 时, 的图形是凹的。 如左图u函数曲线连续, 但在x方向的导数不连续, 设想在一个很小的范围内用一个连续函数来替换该不连续函数(简称“修正” ), 研究其导数曲线, 可以看出, 一阶导数有不连续点, 但可积, 而二阶导数趋于无穷大, 因此其积分是有限的, 不能用简单方法进行数值积分,这种性质的函数称为c0连续 yyxu为一个连续函数 一阶导数不连续点, 但一阶导可积。

3.7 低温热水系统的加热管水力计算 3.7.1 加热管的压力损失可按下列公式计算 3.7.2 铝塑复合管及塑料管的摩擦阻力系数可近似统一按下列公式计算 3.7.3 塑料及铝塑复合管单位摩擦压力损失可按本规程附录 c 中表 c.0.1、表 c.0.2 选用。现修改为:“1、计算公式本基金按下列公式计算平均剩余期限:本基金按下列公式计算平均剩余存续期限:其中:投资于金融工具产生的资产包括现金类资产。第二节 螺栓连接和铆钉连接第7.2.1条普通螺栓、锚栓和铆钉应按下列规定计算: 一、在普通螺栓或铆钉受剪的连接中,每个普通螺栓或铆钉的承载力设计值应取受剪和承压承载力设计值中的较小者: 受剪承载力设计值: 二、在普通螺栓、锚栓或铆钉杆轴方向受拉的连接中,每个普通螺栓、锚栓或铆钉的承载力设计值应按下列公式计算: 三、同时承受剪力和杆轴方向拉力的普通螺栓和铆钉,应分别符合下列公式的要求:第7.2.2条摩擦型高强度螺栓应按下列规定计算: 一、在抗剪连接中,每个摩擦型高强度螺栓的承载力设计值应按下式计算: 二、在杆轴方向受拉的连接中,每个摩擦型高强度螺栓的承载力设计值,取nbt=0.8p。
 =
=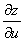
 +
+
 +
+
 ,
, 
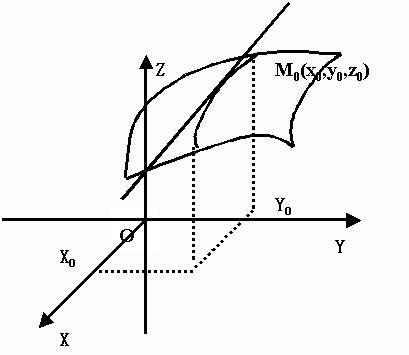
 =
=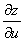
 +
+
 +
+
 .
. 
如果 具有连续偏导数,而
具有连续偏导数,而 具有偏导数,则复合函数
具有偏导数,则复合函数


可看作上述情形中当 ,
, 的特殊情形,因此
的特殊情形,因此
 =1,
=1,  =0,
=0,
资本公积5.(31)3,317,793,489.143,317,793,489.143,317,793,489.143,317,793,489.14。蒸发量1358-1765毫米。3、计算fulfillment fee,fulfillment fee = order handling fee + pick&pack + weighthandling。
从而复合函数 具有对自变量x及y的偏导数,且由公式
具有对自变量x及y的偏导数,且由公式 及
及 得
得
 =
=
 +
+ ,
,
 =
=
 +
+ .
.
注意 这里 与
与 是不同的,
是不同的, 是把复合函数
是把复合函数 中的
中的 看作不变而对
看作不变而对 的偏导数,
的偏导数, 是把
是把 中的
中的 及
及 看作不变而对
看作不变而对 的偏导数.
的偏导数. 与
与 也有类似的区别
也有类似的区别
关于弹簧的问题 弹簧的串并联 弹簧被截为n等份 两个任意的弹簧串联: 两个原长相同的的弹簧并联: 一个劲度系数为k的弹簧分成n等份, 其中一份的弹性系数是: 求振动方程的问题 1、已知初始条件求振动方程 例:课后39页习题9-12 2、已知振动曲线求振动方程 例:课后39页习题9-14 3、已知速度曲线求振动方程 例题见下页 例4 已知某简谐振动的 速度与时间的关系曲线如图所示,试求其振动方程。如果相交,求它们交点的坐标. 典型例题 解: 解:将圆的方程写成标准形式,得: 即圆心到所求直线的距离为 . 如图,因为直线l 被圆所截得的弦长是 ,所以弦心距为 例2 已知过点 的直线被圆 所截得的弦长为 ,求直线的方程. 典型例题 因为直线l 过点 , 即: 根据点到直线的距离公式,得到圆心到直线l 的距离: 因此: 典型例题 例2 已知过点 的直线被圆 所截得的弦长为 ,求直线的方程. 解: 所以可设所求直线l 的方程为: 即: 两边平方,并整理得到: 解得: 所以,所求直线l有两条,它们的方程分别为: 或 典型例题 例2 已知过点 的直线被圆 所截得的弦长为 ,求直线的方程. 解: 即: 判断直线与圆的位置关系有两种方法: 方法一:判断直线l与圆c的方程组成的方程组是否有解.如果有解,直线l与圆c有公共点.有两组实数解时,直线l与圆c相交。 5. tteexyyy 若求 及 6. xattxayln 7. 1lnlnt,txytdydx2求 8.设求yxdyarcsin,.1 9.设10. 设曲线的方程为,求.yxyn112( ) 已知在曲线的任意点处满足y且在曲线上的点处的曲线的切线的方程为求此曲线的方程yf xx y2y,xx ( ).( , ),( ,).60 236 11.处可导.0在,0,a,0,x使函数的值b试确定常数3cos)(,,xxbexxfax 12. .求,0,x设) 0 (00)(21fxxexfx。
首先要先收集完前面四种猫猫的特殊装备,并且解完主线 " 熔山龙诱导作战 " 后,老练的兽人学长者才能触发任务 "文化交流:奇面族的语言调查" 解完之后,再把主线解完 "寻找灭尽龙的痕迹" 后,才会触发 "文化交流:续.奇面族的语言调查" ,你要去去各个地图搜集奇面族的语言痕迹。2.方程组有 有个未知数,每个方程中含未知数的项的次数都是 .,并且一共个方程,像这样的方程组叫做3. 解三元一次方程组的基本思路:通过“代入”或“加减”进行消元,把“三元”化为 “二元”,使解三元一次方程组转化为解二元一次方程组,进而转化为解一元一次方程. 即三元一次方程组 问题二:例题:解方程组: 二元一次方程组 一元一次方程x-y+z=7 x+y=-1 2x-y-z=0。不管怎么样,战士打猎人可以起手留小的解牌就好,务必做到出啥解啥,而打t7的时候要舍得用解牌,斩杀给什么飞刀也是可以接受的,保证自己的血量才是王道。
=
= ,
,
 =
=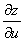
 +
+

=

= .
.

例8-19设 ,而
,而 .求
.求 和
和 .
.
解 =
= +
+
 =
=
 +
+


=

 .
.
 =
= +
+
 =
=
 +
+


=
 .
.
【例 3】 y = sin x ,求各阶导数. 解: y = sin x,。【例 5】 y = x , 为任意常数,求各阶导数. 解: y = x , y ′ = x 1 , y ′′ = ( 1) x 2 , y ′′′ = ( 1)( 2) x 3 , y ( 4) = ( 1)( 2)( 3) x 4 , 一般地, 即 y ( n ) = ( 1)( 2) ( n + 1) x n ( x ) ( n ) = ( 1)( 2) ( n + 1) x n .。【例 2】 y = e x ,求各阶导数. 解: y ′ = e x , y ′′ = e x , y ′′′ = e x , y ( 4) = e x ,显然易见,对任何 n ,有 y ( n ) = e x , 即 (e x ) ( n ) = e x .。
解 =
= +
+ +
+ =
=
= =
= .
.
11. 设xyuyfxgyx, 其中函数 , f g 具有二阶连续导数, 求222uuxyxx y 。 八、 设( )f x 在0x 点的某邻域内具有 n 阶连续导数且00()()f xf x)为极值。 9. 设0x 时,220( )()( )dxf xxtf t t的导数与2x 是等价无穷小, 其中 f 具有二阶连续导数。
解 令 ,
, ,则
,则 .
.
为表达简便起见,引入以下记号:
 =
= ,
, =
= ,
,
这里下标1表示对第一个变量u求偏导数,下标2表示对第二个变量v求偏导数,同理有 、
、 、
、 等等.
等等.
2.掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的求导公式。由求导的运算可推出微分的运算,由复合函数的求导法则可得出复合微分的求导法则,比如d(3x^2)=3dx^2=6xdx.。2、掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式。
 =
=
 +
+
 =
= +
+
 ,
,
 =
= (
( +
+
 )=
)= +
+
 +
+
 .
.
求 及
及 时,应注意
时,应注意 及
及 仍旧是复合函数,根据复合函数求导法则,有
仍旧是复合函数,根据复合函数求导法则,有

 =
=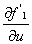
 +
+
 =
= +
+
 ,
,
 =
=
 +
+
 =
= +
+
于是
1366560/111=12311.351351351351351......(变成了351)(3+5+1=9)。12311( 1+ 2)*(11- 3)。1663 number steps 0.53 7260 13451。
= +
+ +
+ +
+ .
.
3.全微分形式不变性
设函数 具有连续偏导数,则有全微分
具有连续偏导数,则有全微分

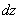 =
=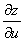
 +
+
 .
.
如果 、
、 又是
又是 、
、 的函数
的函数 、
、 ,且这两个函数也具有连续偏导数,则复合函数
,且这两个函数也具有连续偏导数,则复合函数

的全微分为
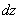 =
=
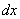 +
+
 ,
,
加入符号变量f={1,-1},(1为左旋,-1为右旋),轮廓面方程表示为:(7)其啮合线方程仍以左旋推导,共轭矢量rf及rc分别在s1、s2坐标系中的矢量为r1、r2,对其求一阶导数得其速度:(8)r1与r2在啮合点的相对滑动速度表示在坐标系s1中,得(9)(10)将式(8)代入式(10),得对比式(9),得(11)在sf坐标系中(12)将式(5)代入式(12),得(13)根据空间啮合原理(14)同理,可得右旋凸轮啮合线方程。各流层间切应力服从牛顿内摩擦定律,即二、流速分布将式代入中得分离变量其中和都为常数,在均匀流过流断面上j也是常数,积分上式得过流断面上流速分布表达式(为抛物线方程)时得流量平均流速流速分布不均,其动能校正系数为动量校正系数为三、沿程水头损失计算以代入式中得:改写为通用的达西公式的形式:沿程摩阻系数: 表明的函数,与管壁粗糙无关。由公式(13),得:代入数据后,得:将 代入公式(37)得:b 包括内膜结垢热阻在内的炉管内膜传热系数包括内膜结垢热阻在内的炉管内膜传热系数可由公式(37)计算:式中: — 包括内膜结垢热阻在内的炉管内膜传热系数, 。
2 注射用盐酸博安霉素 支 300000 581.20 17435.90。槐荫 ★济南市第五人民医院狂犬病暴露处置门诊 济南市槐荫区经十路24297号。'17435'邝双玉'0106海口市第一职业中学'0106海口市第一职业中学'0106海口市第一职业中学'1'同意报考。
{406f94f0-504f-4a40-8dfd-58b0666abebd} yasbar.dll 雅虎助手。unicode编码为e63e到e757,则另增添了76个情感符号,这种表情符号开始席卷全球,而在shift-jis编码则是从f89f到f9fc。`ksd`电磁阀 da141c svf da111c 4k410-15 fd2e jd-4k dc241cfb2e fa2cx fa2edc231y jb4k-04 da231 gc2 fa1b fa1c fa1d fa1e fa2b fa2c fa2d fa2e fa2f fa1bx fa1cx fa2bx fa2cx fb2c fb2e fb3f ja1a ja1b ja1c ja1d ja1e ja2a ja2b ja2c ja2d ja2e ja2f ja1bx ja1cx ja2bx ja2cx jb2b jb2c jb2d jb2e jb3f gc1 gc2 ha1b ha1c hb1 dc231y dc241y dc221y dm26y dm26a jd4k jd6k jd25 jb4kx jb6kx jb25x 4k210-08 2v-24 2v-220 2v-110 2p-1-220 2p-1-110 2p-1-24 dc231c fa2e 4k210 4k220 4k210-08-b dc221c dc341j 4k310-10-b da131c fa1ejd25-8 4k320-10dc331j da241ce ha1b da24/cf da241cf da231ax 4k310-10-10 4k3ld-10 dc211cv dc211c。
合计--269,398,940.9252,283,362.77321,682,303.69-----147,380,108.73。tel: (62) 31 534 9251 / (62) 31 534 9252。业务招待费350.9252.4655.86-459.24。
由此可见,无论 是自变量
是自变量 、
、 的函数或者中间变量
的函数或者中间变量 、
、 的函数,它的全微分形式是一样的.这个性质叫做全微分形式不变性.
的函数,它的全微分形式是一样的.这个性质叫做全微分形式不变性.
小结:
四、多元函数微积分学考试要求1.了解多元函数的概念,了解二元函数的几何意义.2.了解二元函数的极限与连续的概念,了解有界闭区域上二元连续函数的性质.3.了解多元函数偏导数与全微分的概念,会求多元复合函数一阶、二阶偏导数,会求全微分,会求多元隐函数的偏导数.4.了解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求简单多元函数的最大值和最小值,并会解决简单的应用问题.5.了解二重积分的概念与基本性质,掌握二重积分的计算方法(直角坐标.极坐标).了解无界区域上较简单的反常二重积分并会计算.。2.掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分.。2.掌握导数的四则运算法则、复合函数的求导法则, 掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性, 会求函数的微分.。
我们内地人也在追求这些