已知二次函数图象的顶点坐标为M(2.0).直线y＝x+2与该

根据几何知识：经过两点能画出一条直线，并且只能画出一条直线，即两点确定一条直线，所以画一次函数的图象时，只要先描出两点，再连成直线即可.一般情况下：是先选取它与两坐标轴的交点：（0，b），.即横坐标或纵坐标为0的点.。已知二次函数的图象经过,两点,且对称轴为直线.设顶点为点,与轴的另一交点为点.。3. 已知二次函数 的图象顶点为（2，－1），与 轴交点坐标为（0，11），则（ ）。

题目列表(包括答案和解析)

已知二次函数图象的顶点是（-1，2），且过点(0，)．

（1）求二次函数的表达式；

（2）画出该二次函数的图象，并指出x为何值时，y随的x增大而增大．

查看答案和解析>>

kx16、如图，直线l1与l2相交于点p，l1的函数表达式y=2x+3,点p的横坐标为-1,且l2交y轴于点a．求直线l2的函数表达式.17、已知如图，一次函数y=ax+b图象经过点、点。6、（2016•达州）如图，已知二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点a（﹣1，0），与y轴的交点b在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x=1．下列结论：。（2）已知一次函数y=kx+n，点p（m，0）是x轴上的一个动点．若在（1）的条件下，过点p垂直于x轴的直线交这个一次函数的图象于点m，交二次函数y=ax+bx的图象于点n．若只有当1＜m＜时，点m位于点n的上方，求这个一次函数的解析式。

（1）求B点的坐标与这个二次函数的解析式；

（2）P为线段AB上的一个动点（点P与A、B不重合），过P点作x轴的垂线与这个二次函数的图象交于D点，与x轴交于点E．设该线段PD的长为h，点P的横坐标为t，求h与t之间的函数解析式，并写出自变量t的取值范围；

（3）在（2）的条件下，在线段AB上是否存在点P，使得以点P、D、B为顶点的三角形与△B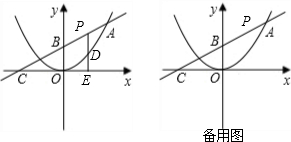OC相似？若存在，请求出P点的坐标；若不存在，请说明理由．

查看答案和解析>>

已知二次函数图象的顶点坐标为M（2，0），直线y=x+2与该二次函数的图象交于A、B两点，其中点A在y轴上（如图示）

（1）求该二次函数的解析式；

（2）P为线段AB上一动点（A、B两端点除外），过P作x轴的垂线与二次函数的图象交于点Q，设线段PQ的长为l，点P的横坐标为x，求出l与x之间的函数关系式，并求出自变量x的取值范围；

（2）当梯形 opfe 的面积等于三角形 apf 的面积时．求线段 pf 的长。（3）以点c为中心，将cd所在的直线顺时针旋转60°交ab边于点e，若以o、c、e、d为顶点的四边形是梯形，求点e的坐标．。16．如图，在平面直角坐标系中，o为坐标原点，a、b、c的坐标分别为(2，4)，(5，0)，(1，0)．p是△oab内（含边界）一点，小明发现如果四边形oapc面积是△oab面积的一半，则点p在一条线段上，则这条线段所在直线的解析式是__________．。

查看答案和解析>>

在已知抛物线与x轴两交点的距离和顶点坐标的情况下，问题比较容易解决．由顶点坐标为（3，-2）的条件，易知其对称轴为x＝3，再利用抛物线的对称性，可知图象与x轴两交点的坐标分别为（1，0）和（5，0）。 北京模拟) 在同一坐标系中，函数y ＝2 x 与 与y＝ ＝12x 的图象之间的关系是的图象之间的关系是( ) y x a ． 关于y 轴对称b ． 关于x 轴对称c ．关于原点对称d ．关于直线y ＝x 对称 解析：∵ ∵y＝ ＝ 12x ＝2－ x ， &there4。3. 已知二次函数 的图象顶点为（2，－1），与 轴交点坐标为（0，11），则（ ）。

（1）求一次函数与二次函数的解析式；

（2）判断以线段AB为直径的圆与直线l的位置关系，并给出证明；

宜宾）如图，一次函数y=﹣x+2的图象与反比例函数y=﹣的图象交于a、b两点，与x轴交于d点，且c、d两点关于y轴对称．。设二次函数的图象与轴交另一点,则二次函数图象上是否存在点(其中)使四边形的面积最大,若存在,求出点的坐标和四边形面积最大值。24．（本题满分10分）如图，一次函数的图象分别交轴、轴于两点，为的中点，轴于点，延长交反比例函数的图象于点d，且od∥ab,（1）求的值。

查看答案和解析>>