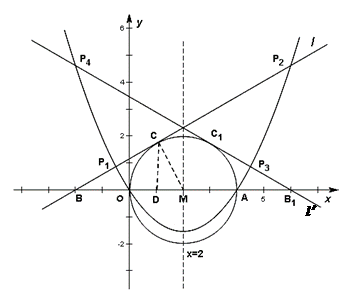
（2013年四川绵阳12分）如图，二次函数y=ax2+bx+

定义：

一般地，如果（a，b，c是常数，a≠0），那么y叫做x 的二次函数。

①所谓二次函数就是说自变量最高次数是2;

②二次函数（a≠0）中x、y是变量，a，b，c是常数，自变量x 的取值范围是全体实数，b和c可以是任意实数，a是不等于0的实数，因为a=0时，变为y=bx+c若b≠0,则y=bx+c是一次函数，若b=0，则y=c是一个常数函数。

③二次函数（a≠0）与一元二次方程（a≠0）有密切联系，如果将变量y换成一个常数，那么这个二次函数就是一个一元二次函数。

二次函数的解析式有三种形式：

（1）一般式：（a，b，c是常数，a≠0）；

（2）顶点式： （a，h，k是常数，a≠0）

（3）当抛物线与x轴有交点时，即对应二次好方程有实根x1和x2存在时，根据二次三项式的分解因式，二次函数可转化为两根式。如果没有交点，则不能这样表示。

二次函数的一般形式的结构特征：

①函数的关系式是整式；

②自变量的最高次数是2；

③二次项系数不等于零。

二次函数的判定：

二次函数的一般形式中等号右边是关于自变量x的二次三项式；

当b=0，c=0时，y=ax2是特殊的二次函数；

为了便于判断函数的奇偶性，有时需要将函数化简或应用定义的等价形式：。要会判断给出的项是否同类项,知道同类项可以合并．即 其中的x可以代表单项式中的字母部分,代表其他式子.。②明确合并同类项的含义是把多项式中的同类项合并成一项,经过合并同类项,式的项数会减少,达到化简多项式的目的。

二次函数的图像

是一条关于对称的曲线，这条曲线叫抛物线。

抛物线的主要特征：

①有开口方向，a表示开口方向：a>0时，抛物线开口向上；a<0时，抛物线开口向下；

②有对称轴；

③有顶点；

④c 表示抛物线与y轴的交点坐标：（0，c）。

二次函数图像性质：

轴对称：

二次函数图像是轴对称图形。已知二次函数图像的顶点坐标c对称轴为直线x=-b/2a

对称轴与二次函数图像唯一的交点为二次函数图像的顶点P。已知二次函数图像的顶点坐标c

特别地，当b=0时，二次函数图像的对称轴是y轴（即直线x=0）。

a,b同号，对称轴在y轴左侧

b=0,对称轴是y轴

a,b异号，对称轴在y轴右侧

顶点：

二次函数图像有一个顶点P，坐标为P ( h,k )

当h=0时，P在y轴上；当k=0时，P在x轴上。即可表示为顶点式y=a(x-h)^2+k。

h=-b/2a， k=(4ac-b^2)/4a。

开口：

二次项系数a决定二次函数图像的开口方向和大小。

当a>0时，二次函数图像向上开口；当a<0时，抛物线向下开口。

|a|越大，则二次函数图像的开口越小。

决定对称轴位置的因素：

一次项系数b和二次项系数a共同决定对称轴的位置。

当a>0,与b同号时（即ab>0），对称轴在y轴左； 因为对称轴在左边则对称轴小于0，也就是- b/2a<0,所以 b/2a要大于0，所以a、b要同号

当a>0,与b异号时（即ab<0），对称轴在y轴右。因为对称轴在右边则对称轴要大于0，也就是- b/2a>0, 所以b/2a要小于0，所以a、b要异号

可简单记忆为左同右异，即当a与b同号时（即ab>0），对称轴在y轴左；当a与b异号时（即ab<0 ），对称轴在y轴右。

事实上，b有其自身的几何意义：二次函数图像与y轴的交点处的该二次函数图像切线的函数解析式（一次函数）的斜率k的值。可通过对二次函数求导得到。

决定与y轴交点的因素:

常数项c决定二次函数图像与y轴交点。

二次函数图像与y轴交于（0,C）

注意：顶点坐标为（h,k)， 与y轴交于（0,C)。

与x轴交点个数：

a<0;k>0或a>0;k<0时，二次函数图像与x轴有2个交点。

k=0时，二次函数图像与x轴只有1个交点。

a<0;k<0或a>0,k>0时，二次函数图像与X轴无交点。

当a>0时，函数在x=h处取得最小值ymin=k，在x<h范围内是减函数，在x>h范围内是增函数（即y随x的变大而变小），二次函数图像的开口向上，函数的值域是y>k

当a<0时，函数在x=h处取得最大值ymax=k，在x<h范围内是增函数，在x>h范围内是减函数（即y随x的变大而变大），二次函数图像的开口向下，函数的值域是y<k

当h=0时，抛物线的对称轴是y轴，这时，函数是偶函数。

二次函数的最值：

1.如果自变量的取值范围是全体实数，则当a>0时，抛物线开口向上，有最低点，那么函数在处取得最小值y最小值=；

当a<0时，抛物线开口向下，有最高点，即当时，函数取得最大值，y最大值=。

也即是：如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当时，。

(4)连线：用平滑曲线，按照自变量由小到大的顺序，把所描各点连接起来．7．一次函数(1)一次函数如果y＝kx＋b(k、b是常数，k≠0)，那么y叫做x的一次函数．特别地，当b＝0时，一次函数y＝kx＋b成为y＝kx(k是常数，k≠0)，这时，y叫做x的正比例函数．(2)一次函数的图象一次函数y＝kx＋b的图象是一条经过(0，b)点和 点的直线．特别地，正比例函数图象是一条经过原点的直线．需要说明的是，在平面直角坐标系中，“直线”并不等价于“一次函数y＝kx＋b(k≠0)的图象”，因为还有直线y＝m(此时k＝0)和直线x＝n(此时k不存在)，它们不是一次函数图象．(3)一次函数的性质当k＞0时，y随x的增大而增大。(3)图象法．6．函数的图象把自变量x的一个值和函数y的对应值分别作为点的横坐标和纵坐标，可以在平面直角坐标系内描出一个点，所有这些点的集合，叫做这个函数的图象．由函数解析式画函数图象的步骤：(1)写出函数解析式及自变量的取值范围。的增大， （1）如果函数在某个区间上随着自变量 的增大， ）如果函数在某个区间上随着自变量x的增大 相应的f(x)也随着增大，我们就说函数在该区间上 也随着增大， 相应的 也随着增大 为增函数。

求二次函数的解析式：

最常用的方法是待定系数法，根据题目的特点，选择恰当的形式，一般，有如下几种情况：

（1）已知抛物线上三点的坐标，一般选用一般式；

（2）已知抛物线顶点或对称轴或最大（小）值，一般选用顶点式；

（3）已知抛物线与x轴的两个交点的横坐标，一般选用两点式；

（4）已知抛物线上纵坐标相同的两点，常选用顶点式。

二次函数的应用：

（1）应用二次函数才解决实际问题的一般思路：

理解题意；

建立数学模型；

解决题目提出的问题。

（2）应用二次函数求实际问题中的最值：

cosh函数计算数字的反双曲余弦值1753应用asin函数计算数字的反正弦值1764应用asinh函数计算数字的反双曲正弦值1775应用atan函数计算数字的反正切值1786应用atanh函数计算数字的反双曲正切值1797应用atan2函数计算x及y坐标值的反正切值1808应用cos函数计算角度的余弦值1819应用cosh函数计算数字的双曲余弦值18110应用degrees函数将弧度转换为度182。窗函数法设计fir滤波器的基本步骤(1) 根据技术要求确定待求滤波器的单位取样响应如果已知待求滤波器的频响：hd(ejw)，则：如果已知通带和阻带衰减和边界频率的要求，可选用理想滤波器作为逼近函数：hd(ejw) —〉 idft —〉hd(n)==〉(2) 根据过渡带及阻带衰减要求，确定窗函数及其长度设过渡带宽为：((，其值近似于窗函数主瓣宽度。六、常微分方程与差分方程考试要求1.了解微分方程及其阶、解、通解、初始条件和特解等概念.2.掌握变量可分离的微分方程.齐次微分方程和一阶线性微分方程的求解方法.3.会解二阶常系数齐次线性微分方程.4.了解线性微分方程解的性质及解的结构定理，会解自由项为多项式.指数函数.正弦函数.余弦函数的二阶常系数非齐次线性微分方程.5.了解差分与差分方程及其通解与特解等概念.6.了解一阶常系数线性差分方程的求解方法.7.会用微分方程求解简单的经济应用问题.。

求最值时，要注意求得答案要符合实际问题。

二次函数的三种表达形式：

①一般式：

y=ax2+bx+c(a≠0,a、b、c为常数)，顶点坐标为 [,]

把三个点代入函数解析式得出一个三元一次方程组，就能解出a、b、c的值。

②顶点式：

y=a(x-h)2+k(a≠0,a、h、k为常数),顶点坐标为对称轴为直线x=h，顶点的位置特征和图像的开口方向与函数y=ax2的图像相同，当x=h时，y最值=k。当k＜0时，y随x的增大而减小．直线y＝kx＋b与y轴的交点坐标为(0，b)，与x轴的交点坐标为 ．(4)用函数观点看方程(组)与不等式①任何一元一次方程都可以转化为ax＋b＝0(a，b为常数，a≠0)的形式，所以解一元一次方程可以转化为：一次函数y＝kx＋b(k，b为常数，k≠0)，当y＝0时，求相应的自变量的值，从图象上看，相当于已知直线y＝kx＋b，确定它与x轴交点的横坐标．②二元一次方程组 对应两个一次函数，于是也对应两条直线，从“数”的角度看，解方程组相当于考虑自变量为何值时两个函数值相等，以及这两个函数值是何值。 x y 函数名称 函数图象 的形状 函数 图象 的 位置 过（0，0),（1 ，k）的一条直线 y随x的增大而减小 函数解析式 函数名称 函数 图象 的 位置 y随x的增大而减小 x 由于两点确定一条直线，画正比例函数图象时我们只需描点(0，0)和点 (1，k)，连线即可. 两点 作图法 用两点法画出下列函数的图象 （1）y= x （2）y=-3x y -4 -2 -3 -1 3 2 1 -1 0 -2 -3 1 2 3 4 5 x y=-3x y -4 -2 -3 -1 3 2 1 -1 0 -2 4 1 2 3 4 -5 x y= x 2 3 3 0 y 2 0 x -3 0 y 1 0 x y=kx (k是常数，k≠0)的图象是一条经过原点的直线 减小 下降 第二、四象限 k＜0 增大 上升 第三、一象限 k＞0 y随x的增大而 从左向右 经过的象限 y=kx 当k<0时，直线y=kx经过第二、四象限，从左向右下降，即随着x的增大y反而减小. 一般地，正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线，我们称它为直线y=kx. 当k>0时，直线y=kx经过第一、三象限，从左向右上升，即随着x的增大y也增大。

有时题目会指出让你用配方法把一般式化成顶点式。

例：已知二次函数y的顶点(1,2)和另一任意点(3,10)，求y的解析式。

解：设y=a(x-1)2+2，把(3,10)代入上式，解得y=2(x-1)2+2。

注意：与点在平面直角坐标系中的平移不同，二次函数平移后的顶点式中，h>0时，h越大，图像的对称轴离y轴越远，且在x轴正方向上，不能因h前是负号就简单地认为是向左平移。 1．空间直角坐标系 ●自主预习 定义 以空间中两两________且相交于一点o的三条直线分别为x轴、y轴、z轴，这时就说建立了空间直角坐标系oxyz，其中点o叫做坐标_______，x轴、y轴、z轴叫做__________．通过每两个坐标轴的平面叫做__________，分别称为xoy平面、yoz平面、________平面 画法 在平面上画空间直角坐标系oxyz时，一般使∠xoy＝__________，∠yoz＝90° 垂直 原点 坐标轴 坐标平面 zox 135° 图示说明 本书建立的坐标系都是右手直角坐标系，即在空间直角坐标系中，让右手拇指指向______轴的正方向，食指指向______轴的正方向，如果中指指向______轴的正方向，则称这个坐标系为右手直角坐标系。【1】用直角坐标系,就是为了让点的表示更简单,从而可以更多的用向量方法去解决问题,所以第一个目标就是让点的坐标写起来更简单,这也是选的标准.所以坐标轴一般应该取平行线较多的线方向,这样点的坐标就容易写出来了.其实看多了例题之后,就会发现,一般直角坐标系的原点都是选多面体的一个顶点,或者取棱的中点.顶点处有直角的,肯定就沿直角方向建立坐标轴了,不是直角的话,就取一条边的方向为x轴或y轴了.如下图示例：。

具体可分为下面几种情况：

当h>0时，y=a(x-h)2的图象可由抛物线y=ax2向右平行移动h个单位得到；

当h<0时，y=a(x-h)2的图象可由抛物线y=ax2向左平行移动|h|个单位得到；

当h>0,k>0时，将抛物线y=ax2向右平行移动h个单位，再向上移动k个单位，就可以得到y=a(x-h)2+k的图象；

当h>0,k>0时，将抛物线y=ax^2向右平行移动h个单位，再向上移动k个单位，就可以得到y=a(x-h)^2+k的图象。当h>0,k<0时，将抛物线y=ax^2向右平行移动h个单位，再向下移动|k|个单位可得到y=a(x-h)^2+k的图象。当h<0,k>0时，将抛物线y=ax2向左平行移动|h|个单位，再向上移动k个单位可得到y=a(x-h)2+k的图象。

当h<0,k>0时，将抛物线y=ax2向左平行移动|h|个单位，再向上移动k个单位可得到y=a(x-h)2+k的图象；

当h>0,k>0时，将抛物线y=ax^2向右平行移动h个单位，再向上移动k个单位，就可以得到y=a(x-h)^2+k的图象。当h>0,k<0时，将抛物线y=ax^2向右平行移动h个单位，再向下移动|k|个单位可得到y=a(x-h)^2+k的图象。当h<0,k<0时，将抛物线y=ax2向左平行移动|h|个单位，再向下移动|k|个单位可得到y=a(x-h)2+k的图象。