2018湖北中考二轮复习二次函数的实际应用

2018湖北中考二轮复习二次函数的实际应用！二轮复习已经来到，根据学习规律，希望同学们能有自己的学习方法。下面是小编为大家整理的2018湖北中考二轮复习二次函数的实际应用，希望对大家有所帮助。二次函数实际应用

2018湖北中考二轮复习知识点实际应用题

考点归纳

归纳1：二次函数与几何的综合运用.

基础知识归纳：求点的坐标，求抛物线解析式，求线段长或图形面积的最值，点的存在性.

基本方法归纳：待定系数法、数形结合思想、分类讨论思想.

注意问题归纳：合理使用割补法表达面积，分类讨论要全面.

1.矩形截面梁 第五节梁的弯曲应力、梁的正应力、剪应力强度条件 式中： 整个横截面对中性轴的惯性矩 b 矩形截面的宽度 距中性轴为 y 的横线以外部分的 横截面面积对中性轴的静矩 其方向与剪力 v的方向相同 z y v 第五节梁的弯曲应力、梁的正应力、剪应力强度条件 第五节梁的弯曲应力、梁的正应力、剪应力强度条件 2.工字形截面梁 腹板上的剪应力 第五节梁的弯曲应力、梁的正应力、剪应力强度条件 v d 3.圆形截面梁和圆环形截面梁 第五节梁的弯曲应力、梁的正应力、剪应力强度条件 4.全梁最大剪应力 统一表达式： 矩形截面： 圆形截面： 环形截面： 第五节梁的弯曲应力、梁的正应力、剪应力强度条件 第五节梁的弯曲应力、梁的正应力、剪应力强度条件 〔例3-9〕图示一矩形截面简支梁，全梁上受均布截荷作用，试计算支座附近截面上b、c两点处的剪应力。例：2011年太平洋冰壶锦标赛在南京奥体中心完美收官.主场作战的中国队表现出色，包揽了男、女两个项目的金牌.如图，冰壶以速度v垂直进入四个矩形区域沿虚线做匀减速直线运动，且刚要离开第四个矩形区域边缘的e点时，速度恰好为零.冰壶通过前三个矩形的时间为t，试通过所学知识计算冰壶通过四个矩形区域所需的时间.。十人九足一、项目类型：团队协作型二、场地要求：一片空旷的大场地三、需要道具：每组一条长约五米的绳子四、详细游戏规则：以系别为单位,共七个队伍。

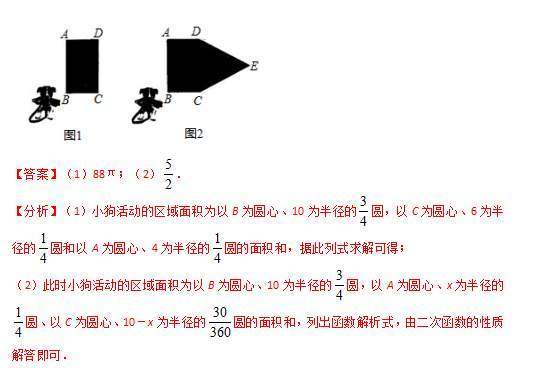
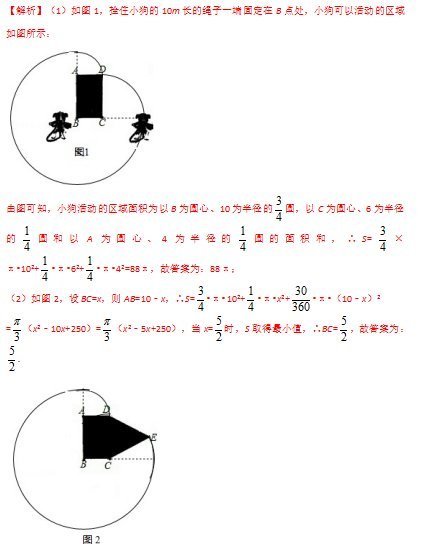
(1)如图1，若BC=4m，则S=m2.

(2)如图2，现考虑在(1)中矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域，使之变成落地为五边形ABCED的小屋，其他条件不变，则在BC的变化过程中，当S取得最小值时，边BC的长为m.

解题思路： 回旋加速器利用电场加速和磁场偏转来加速粒子，带电粒子在磁场中运动的周期与带电粒子的速度无关．根据洛伦兹力提供向心力得出轨道半径的公式，从而根据速度的关系得出轨道半径的关系．粒子离开回旋加速度时的轨道半径等于d形盒的半径，根据半径公式求出离开时的速度大小，从而得出动能．解题过程： 最终答案：abd。点评：此题考查了扇形的面积计算、垂径定理及圆周角定理，解答本题关键是根据图形得出阴影部分的面积等于扇形obd的面积，另外要熟记扇形的面积公式．8．（4分）已知点a（0，2），b（2，0），点c在y=x的图象上，若△abc的面积为2，则这样的c点有（a．1个b．2个c．3个d．4个。 教学开始，我演示平行四边形的面积推导作为本节课的导入，平行四边形的推导的核心就是把一个陌生的平面图形拆分为几个学生熟悉的图形，简而言之就是拆与合，把这种方法引入圆的面积推导之中，是可行的，我首先向学生展示了一个完整的圆，接着向学生展示了把圆折成大小相等十六份，请学生把准备好的圆同样拆成大小相等的十六份，拆完之后，观察每一份的特点，是一个近似于三角形的扇形，之后，把这些小图形合起来，组合成一个自己曾学过的图形，他们组合成了一个长方形，利用长方形的面积计算公式我们推导出了圆的面积公式。

考点：相似三角形的判定与性质．专题：压轴题．分析：采用一般到特殊的方法．解答中首先给出一般性结论的证明，即当eq=kcq（k＞0）时，y与x满足的函数关系式为：y=6k－x。求证：bc=dc．【考点】全等三角形的判定与性质．【专题】证明题．【分析】先求出∠acb=∠ecd，再利用“角边角”证明△abc和△edc全等，然后根据全等三角形对应边相等证明即可．【解答】证明：∵∠bce=∠dca，∴∠bce+∠ace=∠dca+∠ace，即∠acb=∠ecd，在△abc和△edc中， ，∴△abc≌△edc（asa），∴bc=dc．【点评】本题考查了全等三角形的判定与性质，求出相等的角∠acb=∠ecd是解题的关键，也是本题的难点．23．如图所示，在四边形abcd中，ac⊥dc，△adc的面积为30cm2，dc=12cm，ab=3cm，bc=4cm，求△abc的面积．【考点】勾股定理．【分析】利用三角形的面积求出ac的长度，在△abc中根据勾股定理逆定理可以得出是直角三角形．面积等于两直角边乘积的一半．【解答】解：在rt△acd中，s△acd= ac·cd=30，∵dc=12cm，∴ac=5cm，∵ab2+bc2=25，ac2=52=25，∴ab2+bc2=ac2，∴s△abc= ab．bc= ×3×4=6cm2．【点评】根据面积求出一直角边的长度，再利用勾股定理逆定理判断出直角三角形，面积就可以求出了．24．等边△abc和等边△ade如图放置，且b、c、e三点在一条直 线上，连接cd．求证：∠acd=60°．【考点】全等三角形的判定与性质。计算时间1236应用timevalue函数计算时间1244综合实战：人事档案管理125第6章数学与三角函数1281数学与三角函数的分类1282数学函数1311应用abs函数计算绝对值1322应用ceiling.math函数按条件向上舍入数值1323应用combin函数计算给定数目对象的组合数1334应用even函数计算取整后最接近的偶数1345应用exp函数计算e的n次幂1356应用fact函数计。

归纳2：二次函数与实际应用题的综合运用

基础知识归纳：待定系数法求抛物线解析式，配方法求二次函数最值.

基本方法归纳：关键是熟练掌握二次函数的性质.

注意问题归纳：在求二次函数最值时一定要准确求出自变量的取值，特别要观察顶点是否在取值范围内，若在，则取顶点纵坐标为最值;若不在，则根据取值范围在对称轴左右和开口方向，利用增减性求最值.

【例2】某超市销售一种牛奶，进价为每箱24元，规定售价不低于进价.现在的售价为每箱36元，每月可销售60箱.市场调查发现：若这种牛奶的售价每降价1元，则每月的销量将增加10箱，设每箱牛奶降价x元(x为正整数)，每月的销量为y箱.

(1)写出y与x中间的函数关系书和自变量x的取值范围;

(2)超市如何定价，才能使每月销售牛奶的利润最大?最大利润是多少元?

【答案】(1)y=60+10x(1≤x≤12，且x为整数);(2)超市定价为33元时，才能使每月销售牛奶的利润最大，最大利润是810元.

【分析】(1)根据价格每降低1元，平均每天多销售10箱，由每箱降价x元，多卖10x，据此可以列出函数关系式;

(2)由利润=(售价﹣成本)×销售量列出函数关系式，求出最大值.

【解析】(1)根据题意，得：y=60+10x，由36﹣x≥24得x≤12，∴1≤x≤12，且x为整数;

(2)设所获利润为W，则W=(36﹣x﹣24)(10x+60)=﹣10x2+60x+720=﹣10(x﹣3)2+810

∴当x=3时，W取得最大值，最大值为810.

答：超市定价为33元时，才能使每月销售牛奶的利润最大，最大利润是810元.

（2）根据利润=（售价-成本）×销售量列出函数关系式。当收入函数和成本函数均可微时，直接对利润函数求一阶导数，即可得到最优售价。∵成本为50元的排球，规定试销期间单价不低于成本价，且获利不得高于40%．∴50≤x≤70，∴当试销单价定为70元时，该商店可获最大利润，最大利润是1000元．（3）依题意得：-x2+170x-6000≥600，解得：60≤x≤110，∵获利不得高于40%，∴最高价格为50（1+40%）=70，故60≤x≤70的整数．点评：本题主要考查二次函数的应用，根据利润=（售价-成本）×销售量列出函数关系式，运用二次函数解决实际问题，比较简单．。

考点：1.二次函数的应用;2.二次函数的最值;3.最值问题.

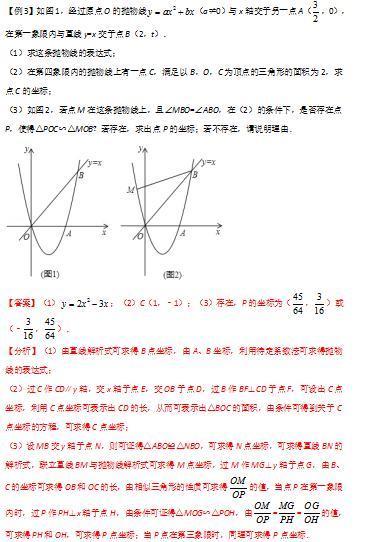
本题为二次函数的综合应用，涉及待定系数法、三角形的面积、二次函数的性质、全等三角形的判定和性质、相似三角形的判定和性质、方程思想及分类讨论思想等知识.在(

1)中注意待定系数法的应用，在(

2)中用

C点坐标表示出

△BOC的面积是解题的关键，在(

3)中确定出点P

考点：1.二次函数综合题;2.存在型;3.分类讨论;4.压轴题.

以上就是小编为大家整理的2018湖北中考二轮复习二次函数的实际应用，同学们还有其他学习上的问题，可拨打爱智康课程免费咨询热线电话：4000-121-121 .那里有专业的老师为大家解答。二次函数实际应用