抛物线的准线方程公式 已知点P是抛物线y2=4x上的点,设点P到抛物线准线的距离为

据魔方格专家权威分析,试题“已知点P是抛物线y2=4x上的点,设点P到抛物线准线的距离为d1,到圆..”主要考查你对抛物线的性质(顶点、范围、对称性、离心率)等考点的理解。抛物线的准线方程公式关于这些考点的“档案”如下:
关于抛物线的几个重要结论:
(1)弦长公式同椭圆.
(2)对于抛物线y2=2px(p>0),我们有P(x0,y0)在抛物线内部 P(x0,y0)在抛物线外部
P(x0,y0)在抛物线外部

(3)抛物线y2=2px上的点P(x1,y1)的切线方程是 抛物线y2=2px(p>0)的斜率为k的切线方程是y=kx+
抛物线y2=2px(p>0)的斜率为k的切线方程是y=kx+

(4)抛物线y2=2px外一点P(x0,y0)的切点弦方程是
(5)过抛物线y2=2px上两点
 的两条切线交于点M(x0,y0),则
的两条切线交于点M(x0,y0),则
(6)自抛物线外一点P作两条切线,切点为A,B,若焦点为F, 又若切线PA⊥PB,则AB必过抛物线焦点F.
又若切线PA⊥PB,则AB必过抛物线焦点F.
利用抛物线的几何性质解题的方法:
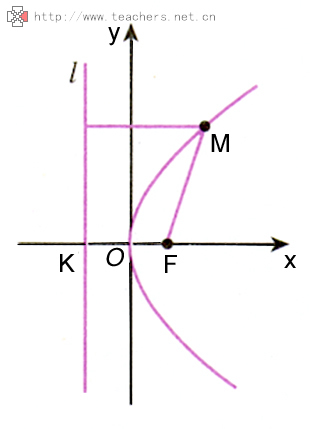
根据抛物线定义得出抛物线一个非常重要的几何性质:抛物线上的点到焦点的距离等于到准线的距离.利用抛物线的几何性质,可以进行求值、图形的判断及有关证明.
抛物线中定点问题的解决方法:
在高考中一般以填空题或选择题的形式考查抛物线的定义、标准方程以及几何性质等基础知识,在解答题中常常将解析几何中的方法、技巧与思想集于一身,与其他圆锥曲线或其他章节的内容相结合,考查综合分析问题的能力,而与抛物线有关的定值及最值问题是一个很好的切人点,充分利用点在抛物线上及抛物线方程的特点是解决此类题型的关键,在求最值时经常运用基本不等式、判别式以及转化为函数最值等方法。
利用焦点弦求值:
利用抛物线及焦半径的定义,结合焦点弦的表示,进行有关的计算或求值。



抛物线中的几何证明方法:
利用抛物线的定义及几何性质、焦点弦等进行有关的几何证明是抛物线中的一种常见题型,证明时注意利用好图形,并做好转化代换。抛物线的准线方程公式
平常人怎么破