有效数字运算规则例子_有效数字的运算规则_有效数字运算规则例子

每个问题计算过程中的小数均保留实际位数，计算结果中不足0.01 元的部分进到0.01元。②混循环小数小数部分化成分数：分子是第二个循环节以前的小数部分的数字组成的数与不循环部分的数字所组成的数之差，分母的头几位数字是9，9的个数与一个循环节的位数相同，末几位是0，0的个数与不循环部分的位数相同。1.加减运算:计算结果的欠准位与各量中欠准位数最高的对齐2.乘除运算:计算结果的有效数字位数和参与运算的各量中有效数字位数最少的相同3.其它运算：乘方、开方、三角函数、对数等函数运算，结果的有效数字位数一般与原函数的有效数字位数相同（对数的首数不作为有效数字）4.参与运算的准确数或常数，其有效数字位数有无限多位，可根据运算需要合理取。

（4）除数是小数的除法，先移动（）的小数点，使它变成（）数，除数的小数点向右移动几位，（）的小数点也向（）移动几位，位数不够的，在（）的末尾用（）补足，然后按照除数是（）数的小数除法进行计算。每个问题计算过程中的小数均保留实际位数，计算结果有小数的，小数保留2 位。1.加减运算:计算结果的欠准位与各量中欠准位数最高的对齐2.乘除运算:计算结果的有效数字位数和参与运算的各量中有效数字位数最少的相同3.其它运算：乘方、开方、三角函数、对数等函数运算有效数字运算规则例子，结果的有效数字位数一般与原函数的有效数字位数相同（对数的首数不作为有效数字）4.参与运算的准确数或常数，其有效数字位数有无限多位，可根据运算需要合理取。

为什么不将各组小数点以后的所有数字都加到总和中呢？下面举一个简单的例子来说明这个问题。

例如，14．75＋0．3676，应以14．75为准，将0．3676化为0．37。

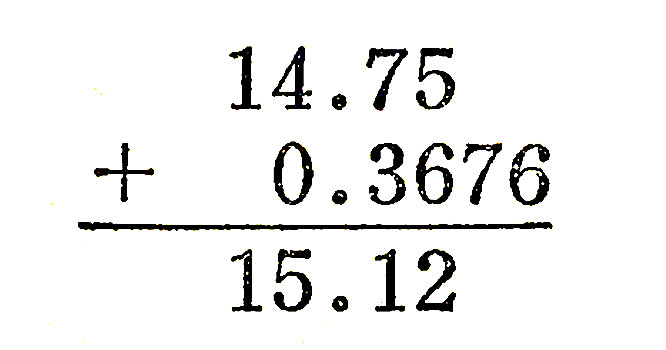
14．75＋0．3676，实际上是（14．75±0．01）＋（0．3676±0．0001），因为14．75中的0．05不是一个绝对准确数，而是一个估计值。在0．3676中的0．0006也是估计值。既然它们是估计值，也可能是0．05，也可能是0．04或0．06；0．0006也可能是0．0007或0．0005。所以，14．75的误差范围最小是±0．01，0．3676的误差范围在±0．0001。这样相加起来的和，就有以下九组数值的可能：

smith首次使用计算机（eniac）计算π，以后的记录都用计算机来计算的2037位小数1953年mahler证明π不是刘维尔数-1955年j。是无理数（则π也是无理数），并提及π是超越数的可能性-1841年rutherford计算了208个小数位，但并非全部是正确的152位小数1844年zacharias dase及strassnitzky200位小数1847年thomas clausen248位小数1853年lehmann261位小数1853年rutherford440位小数1853年william shanks527位小数1855年richterout500位小数1874年en:william shanks耗费15年计算了707位小数，可惜1946年d。 smith100000位小数1966年250000位小数1967年500000位小数1974年1000000位小数1981年金田康正2000000位小数1982年4000000位小数1983年8000000位小数1983年16000000位小数1985年bill gosper17000000位小数1986年david h。

因此，我们就可以得出一个结论：带有小数的几组数相加或相减时，所得的和或差的有效数值有效数字运算规则例子，应以小数点后位数最小的那一组数的位数来确定。

减法的运算法则与加法相同。如，0．13752－0．0008＝0．1367。

在计算几组数字相乘或相除时，各组数字保留的位数，应以百分误差最大或有效数字位数最少的那一组数为标准，所得乘积或商的准确度，不应大于精确度最小的那一组数。

例如，12．72×0．045

12．72实际上是12．72±0．01，其百分误差头0．01/12．72×100＝0．078％，0．045实际上是0．045±0．001，其百分误差为0．001/0．045×100＝2．2％。0．045的百分误差2．2％比12．72的百分误差0．078％大得多，也就是说，在0．045中只要相差0．001就有2．2％的误差，尽管12．72再准确早已被0．045的误差掩盖了。所以这两组数值相乘积的有效数字，应以0．045的两位有效数字为准来确定。即：

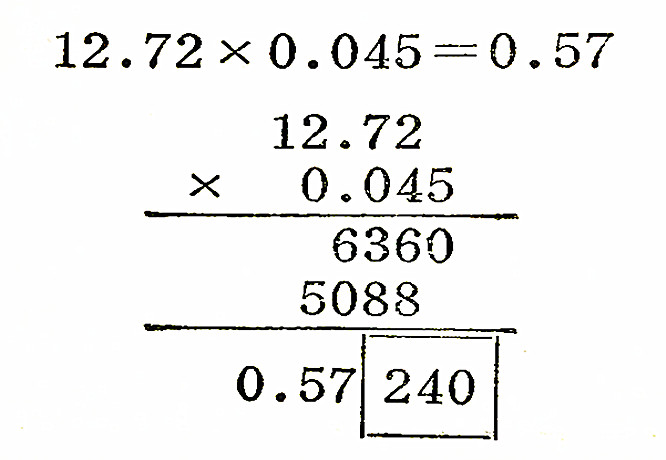
例，0．001234×0．015＝1．8×10（-5次方）即以0．015两位有效数字为准。

0．515÷0．464＝1．11。两组数都是三位有效数字，商也应为三位有效数字。

由上述各例的运算可以看出，加减乘除的所得结果有效数字的确定，可按位数最少那一组数的位数来确定。