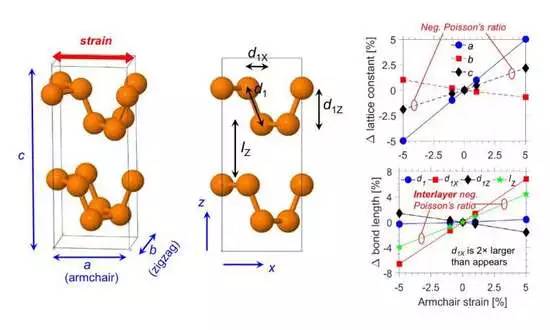
模拟线弹性材料能有多难？

复投影平面中代数曲线的研究是几何应用如密码技术研究的重要内容，也是线性几何研究向代数几何研究的自然过渡。 （2） 由求解线性工程问题进展到分析非线性问题[8] 随着科学技术的发展， 线性理论已经远远不能满足设计的要求， 许多工程问题如材料的破坏与失效、 裂纹扩展等仅靠线性理论根本不能解决， 必须进行非线性分析求解，例如建筑行业中的高层建筑和大跨度悬索桥的出现, 就要求考虑结构的大位移和大应变等几何非线性问题。而且还可以消除一般弹性材料因过大压缩而引起弹性疲劳的特点c、使用遇水膨胀橡胶作为堵漏密封止水材料，不仅用量节省，而且还可以清除一般弹性材料因过大压缩而引起弹性疲劳的特点，使防水效果更可靠，耐水性，耐化学性能和耐老化性能良好。

各向同性线弹性

26附录e 二极管参数汇总 329附录f 三极管参数汇总 331附录g 场效应管参数汇总 334附录h 常用三极管性能参数表 337附录i 常用运算放大器性能参数表 338附录j 常用敏感电阻 339参考文献 341。6、计算所用元器件型号与参数7、对电路进行仿真进度安排 起止日期 工作内容 备注 1、根据课题，查阅相关资料2、画出系统原理框图3、参数计算和元器件选择4、画出单元电路5、画出整体电路图6、进行模拟仿真7、撰写课程设计报告。6、计算所用元器件型号与参数7、对电路进行仿真进度安排 起止日期 工作内容 备注 根据课题，查阅相关资料画出系统原理框图参数计算和元器件选择画出单元电路画出整体电路图进行模拟仿真撰写课程设计报告。

杨氏模量、剪切模量和泊松比

附录： 1、 表.1 巴特沃斯归一化低通滤波器参数 n=1 ， 极点 -1 n=2 ， 极点 -0.707+j0.707 -0.707-j0.707 n=3 ， 极点 -0.5+j0.866 -0.5-j0.866 -1 n=4 ， 极点 -0.3827+j9239 -0.3827-j9239 -9239-j0.3827 -9239-j0.3827 2、 表 2 6 种窗函数的基本参数 窗函数类型 过渡带宽度 阻带最小衰减（db） 窗函数公式 汉宁窗 6. 2&pi。当负荷参数采用总污泥量综合设 计法的公式推算值时，则所得sbr 池容趋于合理、偏差缩小，但仍然存有Δh、hmax 参数与沉降速度、沉淀面积及保护高度之间的关系相脱节的缺陷，最终将影响处理效果。88 金属杨氏模量、 弦线模量、 切线模量和泊松比试验方法(静态法)gb/t 4157&mdash。

杨氏模量可以通过单轴拉伸试验直接测量，而剪切模量可以通过纯扭试验测量。

在单轴试验中，泊松比用于确定材料的横向收缩（或拉升）程度。其容许范围为 -1 << 0.5，当其为正值时，表示材料受拉时会在厚度方向上发生收缩。有一些材料具有负泊松比，它们被称为 Auxetics。葡萄酒瓶中软木塞的泊松比接近于零，所以无论是拔出或推入，它的直径都不受影响。不可压缩材料的泊松比

对于大部分金属和合金而言，1/3，所以剪切模量大约等于杨氏模量的 40%。

在给定 的可能取值后，剪切模量和杨氏模量的比值范围为

当 接近 0.5 时，材料变得不可压缩，此类材料会给分析带来特定问题，我们将在下文说明。

体积模量

体积模量 反映一定均匀压力下的体积变化。它可以用杨氏模量 和泊松比 推导出来，表示为：

当 = 1/3 时，体积模量与杨氏模量的值相等，但是对于不可压缩材料（0.5）， 趋近无穷。

体积模量往往与剪切模量被一起指定。从某种意义上讲，这两个参数是最独立的参数选择。体积变化仅仅取决于体积模量，扭曲则完全受剪切模量决定。

拉梅常数

拉梅常数 和 常见于论述弹性的数学论文。我们可以用拉梅常数方便地表述应力张量 和应变张量 间的全三维本构关系：

常数 即为剪切模量， 则可以写为

。

线弹性材料的不可压缩性

ub 土骨架的有效附加应力 孔隙流体的体积压缩变化 孔隙流体的体积压缩系数为cf ，单位孔隙压力作用引起的体应变 土骨架的体积压缩变化 设土骨架的体积压缩系数为cs 体积v 线弹性体 附加应力情况－等向压缩应力状态 §3.5 土的有效应力原理 3.5.2 饱和土中孔隙水压力和有效应力的计算 孔压系数b 附加应力情况－等向压缩应力状态 不排气不排水条件： 。3 土骨架体积压缩系数cs 流体体积压缩系数cf 求解方法：虎克定律 孔压增加使流体体积压缩 有效应力增加使土骨架体积压缩 二者体积变化量相同 问题： 如何求解。v 土骨架的体变等于孔隙流体的体变 体积v §3.5 土的有效应力原理 3.5.2 饱和土中孔隙水压力和有效应力的计算 cf: 孔隙流体的体积压缩系数，单位孔隙压力作用引起的体应变 cs: 土骨架的体积压缩系数 附加应力情况－等向压缩应力状态 饱和土： 干 土： 非饱和土： 孔压系数b是反映土饱和程度的指标 0.2 0.4 0.6 0.8 1.0 sr 1.0 0.8 0.6 0.4 0.2 0 b §3.5 土的有效应力原理 3.5.2 饱和土中孔隙水压力和有效应力的计算 附加应力情况－偏差应力状态 线弹性体 基本假设：土骨架为线弹性体 流体压力处处相等 已知条件：不排气不排水条件 偏差应力。

不成立，而必须用一个约束说明进行替代

8 2 方程 x+4 -(x-5)= x+3 - x-2 中含有分数和括号, 所以要解这个方 5 3 2 程, 首先必须找出分母的最小公倍数 , 利用等式的性质 2, 方程两边 去分母, 得 6(x+4)-30(x-5)=10(x+3)-15(x-2), 要求 k 的值, 必须先知道 x 的值, 而 x 是方程 x+4 5 同乘以这个最小公倍数即可去分母, 然后去括号、 移项、 合并同类项 和系数化为 1。分母相同， 由方程组的四个系数确定分母相同， 由方程组的四个系数确定。 5. tteexyyy 若求 及 6. xattxayln 7. 1lnlnt,txytdydx2求 8．设求yxdyarcsin,.1 9．设10． 设曲线的方程为，求．yxyn112( ) 已知在曲线的任意点处满足y且在曲线上的点处的曲线的切线的方程为求此曲线的方程yf xx y2y,xx ( ).( , ),( ,).60 236 11.处可导．0在，0，a，0，x使函数的值b试确定常数3cos)(,,xxbexxfax 12. ．求，0，x设) 0 (00)(21fxxexfx。

想法可行，但在这种情况中，基于标准位移的有限元公式可能得出不理想的结果，这是由锁定现象引起的。造成的后果包括：

首先在【控制面板】-【程序】-【启用或关闭windows功能】中看到我们的hyper-v前面的框是个方块，并不是个勾，这表明我们的hyper-v功能并没有全部选用。3)稍等片刻，出现'windows功能'选项框，将里面的'远程差分压缩'选项的勾去掉，然后点'确定'，之后重启计算机，重新测试传输速度。iis6.0配置使用gzip压缩页面文件 使用gzip压缩页面文件,既可以降低站点流量,减轻服务器负担,又可以提高用户打开页面的速度,是非常有优势的.要启用gzip压缩,既可以在页面程序中设置(见),也可以在iis服务器中设置,今天我们看看怎么在iis6.0中配置使用gzip压缩. 3步开启iis6.0gzip压缩功能 ①在iis中打开网站属性,切换到"服务"选项卡,钩选"压缩应用程序文件"和"压缩静态文件。

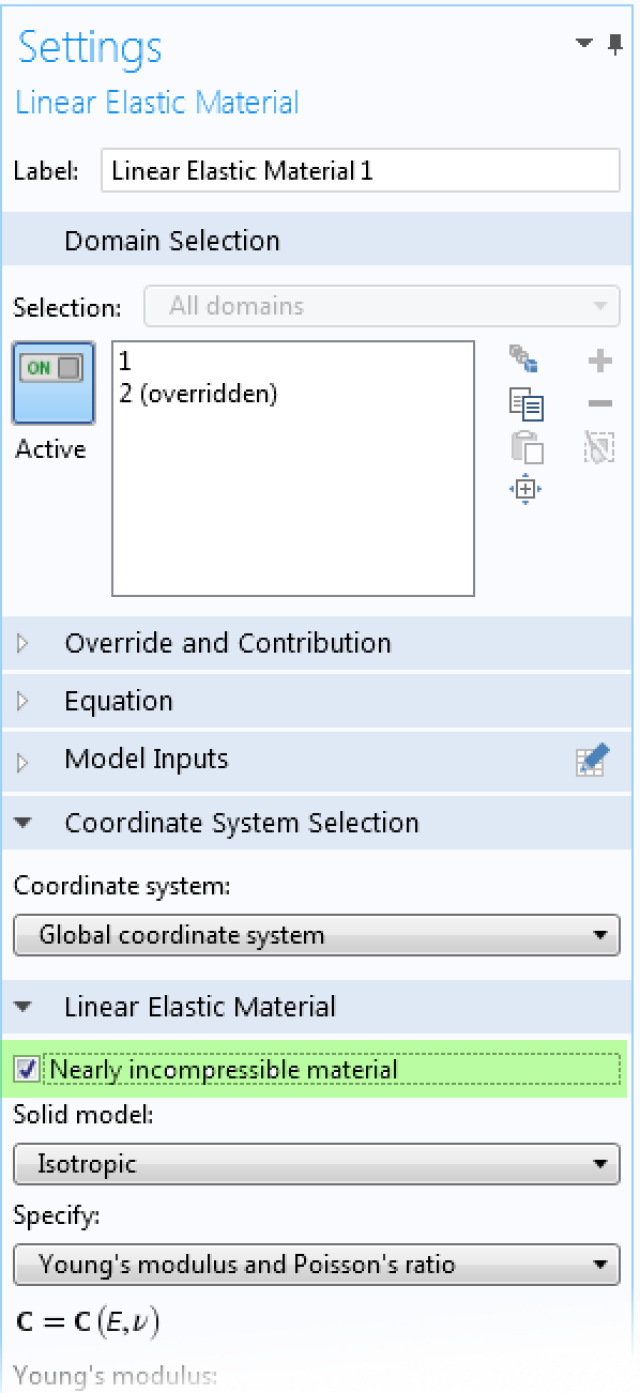
为线弹性材料启用混合公式的部分设置。不可压缩材料的泊松比

当泊松比约大于或等于 0.45 时，体积模量比剪切模量大超过一个数量级，因此使用混合公式是明智的做法。其效果示例如下图所示。

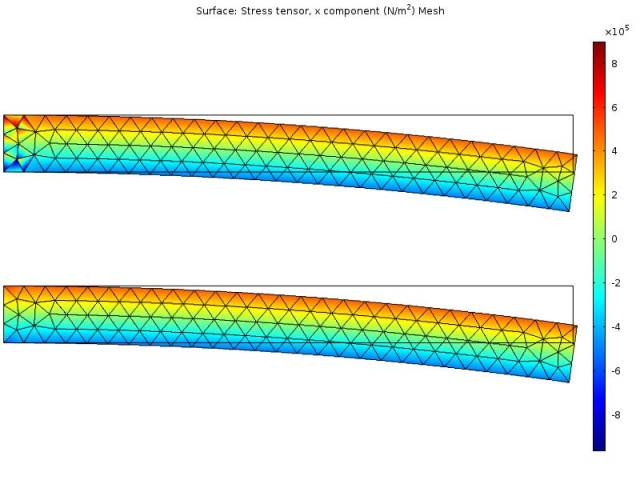
一个简单的平面应变模型中的应力分布，= 0.499。上方的图表示基于标准位移的方程，下方的图表示混合方程。

在仅涉及位移自由度的解中，其应力分布图在左端（即存在约束的位置）呈现出扭曲的状态。使用混合公式后，这些扭曲几乎全部消失。

正交各向异性和各向异性

小变形弹性本构关系 均匀材料的小变形弹性本构关系均 6 chapter 2.1 匀材料的小变形线弹性本构关系 各向同性弹性体 假设物体是均匀、连续、各向同性的，应力和应变间的关系只决定于物体的物理性质，应力和应变之间的关系与坐标的位置和方向无关。满足以上要求的电阻应变片的种类很多#具体选择应变片尺寸时应考虑应力分布$动静态测选用时还要根据弹性体的结构$应力状态$材料$使量$弹性体应变区大小等因素%若材质均匀$应力梯用环境条件$以及电阻应变片的阻值$尺寸$蠕变匹度大#应选用栅长小的应变片#若材质不均匀而强度配等因素#综合考虑选用合适的应变片#一般来说不等的材料。 应力主轴与全量应变主轴重合 弹性变形是可逆的，与应变历史（加载过程无关），应力与应变之间存在统一的单值关系. 弹性变形时，应力张量使物体产生体积变化，泊松比小于0.5. 弹性变形时的应力应变关系的特点 * 体积不变，泊松比v=0.5 5.2 塑性变形时应力应变关系特点 应力、应变为非线性关系 全量应变与应力主轴不一定重合 塑性变化不可逆——无单值一一对应关系——与加载路径有关 对于应变硬化材料，卸载后的屈服应力比初始屈服应力高。

幸运的是，各向异性材料通常会表现一定的对称性。在正交各向异性材料中，有三个正交方向上的剪切作用和轴向动作实现解耦。也就是说，当材料沿着其中一个主方向拉伸时，它只会在两个正交方向上收缩，而不会受剪切力的作用。完整描述正交各向异性材料需要九个独立材料参数。

当以柔度形式记录时，正交各向异性材料的本构关系会更加清晰明了，其中 ：

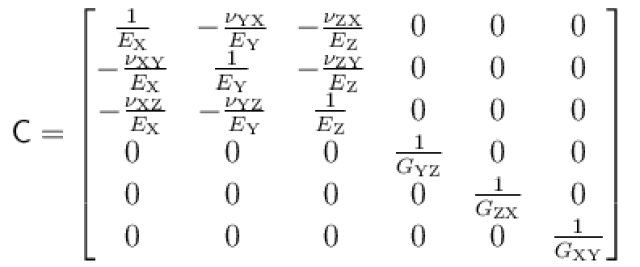
由于柔度矩阵必然是对称的，因此使用的十二个常数可通过符合下方形式的三个对称关系减少为九个

发生通胀时，工人一开始 就有预期，且预期值与实 际通胀发生值相同。如果我们使用“数值”纹理无论是什么方式（像凹凸贴图，置换贴图，或任何一个比实际颜色更需要纹理填充的地方），我们都不得不为了精确的“数值”，去改变前面的gamma校正节点，从而关闭它的内部结构来弥补我们所期望得到的gamma值，将其填充进gamma校正属性里面（注意：这个属性并不代表实际的颜色值^gamma功能，它在一定程度上象征了我们所期望弥补的gamma数值，也就是说，“反相”，或者让gamma值交互左作用，---没有人总会告诉你这些知识，但是你可以现在把它学好）。x y压型钢板 lyxl(a)正交异性板lyμlyx μ/mym x xl l(b)等效各向同性板（计算 mx 时） (c)等效各向同性板（计算 my 时）图 5.1.4 双向正交异性板的计算边长5.1.5 连续组合楼板在强边方向正弯矩作用下，采用弹性分析计算内力时，可考虑塑性内力重分布，但支座弯矩调幅不宜大于 15%。